湖北省新冠肺炎确诊人数的建模与预测分析

白 璐 郭佩汶 范晋蓉

(大连民族大学理学院 辽宁大连 116600)

1 前言

2020 年初，武汉暴发新型冠状病毒（2019-nCoV）肺炎（COVID-19）疫情。随着研究的进展，钟南山院士宣布新冠病毒可以人传人，主要通过呼吸道飞沫传播与接触传播。病毒短短几日席卷湖北省乃至全国，各地开始采取一些防控措施，如呼吁民众戴口罩、勤洗手、避免聚集性活动等。本文利用湖北省疫情初步暴发至采取封城措施后的一个月内每日确诊人数的数据，经过数据预处理、模型识别、参数估计、模型验证与模型优化等时间序列分析方法[1-3]，建立与之对应的时间序列模型，并对模型进行具体解释。最终利用该模型对湖北省未来确诊人数进行6 期预测分析，以期为疫情防控提供数据支持。

2 资料与方法

2.1 数据资料

数据来自搜狗新型冠状病毒（简称“新冠”）疫情实时动态数据统计[4]。

根据该网站公布的数据，收集了2020 年1 月25 日—2020 年3 月4 日湖北省每日确诊人数的数据。

2.2 研究方法

疫情期间，湖北省每日确诊人数数据是十分典型的时序数列，且极大程度反映了疫情传播情况与影响力，“封城”政策实行后的数据更能反映对疫情的控制力度，通过数据预测，能科学具体地观测到疫情的发展趋势。因此，基于随机过程理论与数理统计学方法，本文采用时间序列分析的方法建模，通过对数据的分析与处理，选用求和自回归移动平均模型（ARIMA）模型进行建模，并作出6 期预测分析。

ARIMA 模型是19 世纪70 年代伯克斯和詹金斯提出的时间序列预测方法，其模型表达式为：

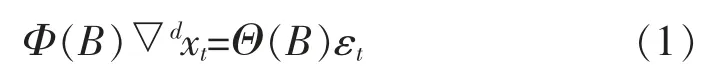
其中，d—求和阶数；Φ（B）=1-φ1B-…-φPBP—平稳可逆 ARMA（p，q）模型的自回归系数多项式；Θ（B）=1-θ1B-…-θqBq—平稳可逆ARMA 模型的移动平均系数多项式。

其建模过程依照如下步骤：

（1）数据预处理：对收集到的数据进行整理使其适用于R 语言处理，并将其调整为时间序列的标准形式。绘制其时序图初步观察其数据走势，如果是平稳时间序列，则其时序图会围绕某一固定值做有界波动。然后做出它的自相关（ACF）图，如果是平稳时间序列，那么它的ACF 图具有迅速衰减的规律。若序列被证明为平稳，还要对它进行白噪声检验（随机性检验）。如果检验得到是白噪声则证明序列之间无相关性，就无法对其进行预测，对它建模也就失去了意义。

（2）数据平稳化：由步骤（1）可知如何处理平稳时间序列，但如果时序图是具有某种趋势的非平稳时间序列，就要提取其确定性趋势项，即对具有随机性趋势的非平稳时间序列做一阶或二阶差分，从而提取其随机趋势，再将差分后的时间序列进行随机性检验。通过检验后，就可以进行ARIMA 拟合建模。需要注意的是，在实际计算中也会有趋势拟合之后数据不平稳的现象，这时就需要使用其他方法处理数据。

（3）模型识别：通过R 语言作时间序列的自相关图观察其拖尾或截尾情况，再作偏自相关图观察拖尾或截尾情况，从而估计其P 值、q 值，即自回归阶数与平均移动阶数的取值[5，6]。

（4）模型估计：这一步骤也称为口径拟合，本文是利用指定参数估计法（条件最小二乘和极大似然估计混合方法）估计模型中的未知参数。

（5）模型检验：检验数据拟合的残差是否是白噪声序列以及是否过度拟合。只有白噪声序列才能通过检验，否则就要返回（2）或（3）重新开始。通过检验后，还要对估计的参数进行显著性检验，精简的模型是指没有不显著参数的模型。

（6）模型优化：这一步是为了选出最有效的模型，本文运用赤池信息准则信息准法（AIC）与贝叶斯信息准则法（BIC）选取最优模型。

（7）预测：根据最优模型做出线性最小方差预测。

3 数据建模过程

3.1 数据预处理

根据湖北省 2020年1 月 20 日—3 月 4 日患新型冠状病毒肺炎（简称“新冠肺炎”）人数的数据绘制时序图，详见图1。由图1 可知，该数据具有明显递增趋势，不具有平稳性数据的特征，需将此数据进行平稳化处理。

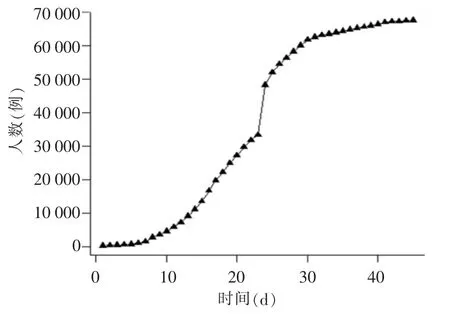
图1 时序图

3.2 数据平稳化

采用差分的方法，对患新冠肺炎人数的数据进行一阶差分，再对一阶差分序列进行白噪声检验。结果表明，一阶差分后的序列为非白噪声，一阶差分序列时序图详见图2。经过一阶差分后，原序列的线形趋势被提取，此时可以先确定ARIMA 模型中的d 值为1。另外，后期的数据是以临床诊断统计的，而非前期的核酸检测，所以导致数据有个跳。

3.3 模型的识别与建立

由一阶差分序列的自相关图和偏自相关图（图3）得出，自相关函数具有拖尾性，偏自相关函数具有一阶截尾性，可将一阶差分序列识别为 ARIMA（1，1，0）。

3.4 参数估计、模型检验及优化

分别对拟定的 4 个模型 ARIMA（1，1，0）、ARIMA（1，1，1）、ARIMA（1，1，2）、ARIMA（0，1，1）进 行“最小二乘-极大似然”参数估计，并对残差进行白噪声检验，拟定的4 个模型的残差检验结果的P 值均远远大于0.05，可认为以上的4 个模型都通过检验。因数据处理与检验均使用R 语言进行，而R 语言给出的参数估计是显著的，可省去参数的显著性检验。比较以上 4 个模型的信息量，发现 ARIMA（1，1，1）模型的信息量 AIC=805.34，BIC=810.70，是 4 个拟合模型中最小的，由此，对 ARIMA（1，1，1）口径拟合，模型如下：

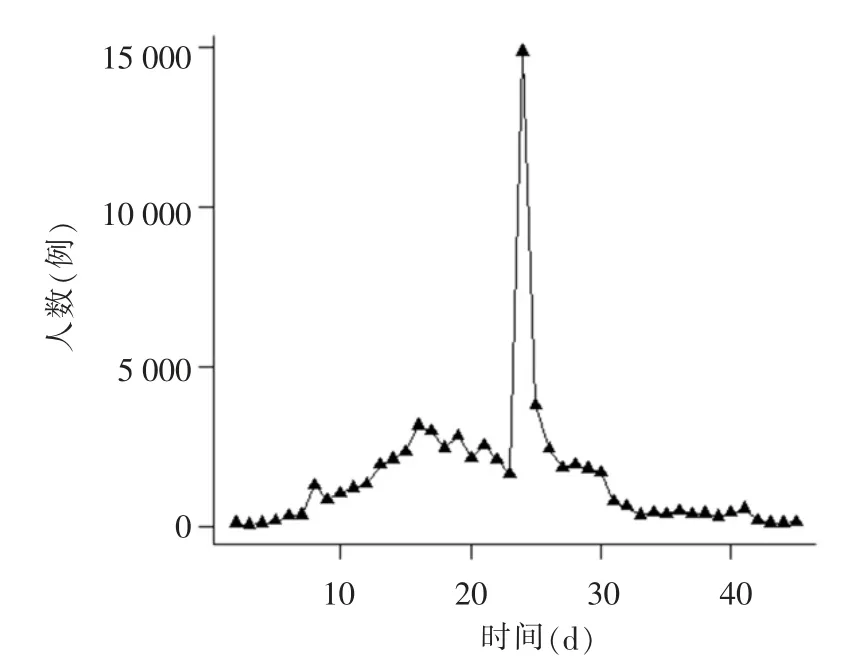
图2 一阶差分时序图

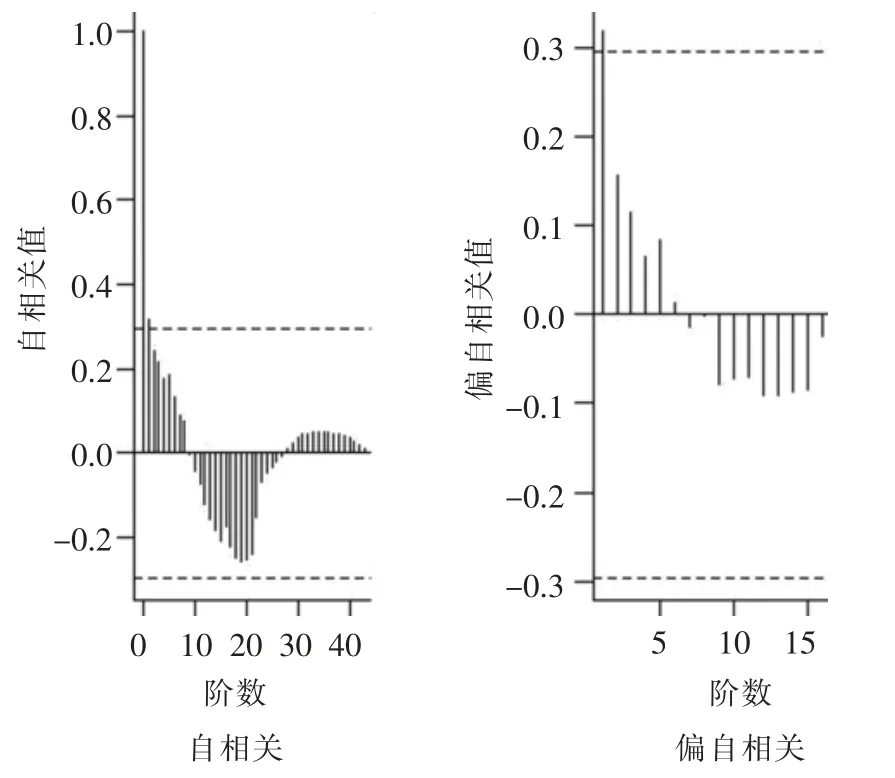
图3 一阶差分序列的自相关图和偏自相关图

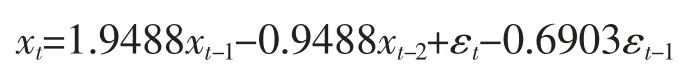
3.5 模型预测及选取

使用建立的模型进行6 期预测，给出预测的80%和95%的置信区间并绘制相应的预测图（图4）和个性化预测图（图5）。

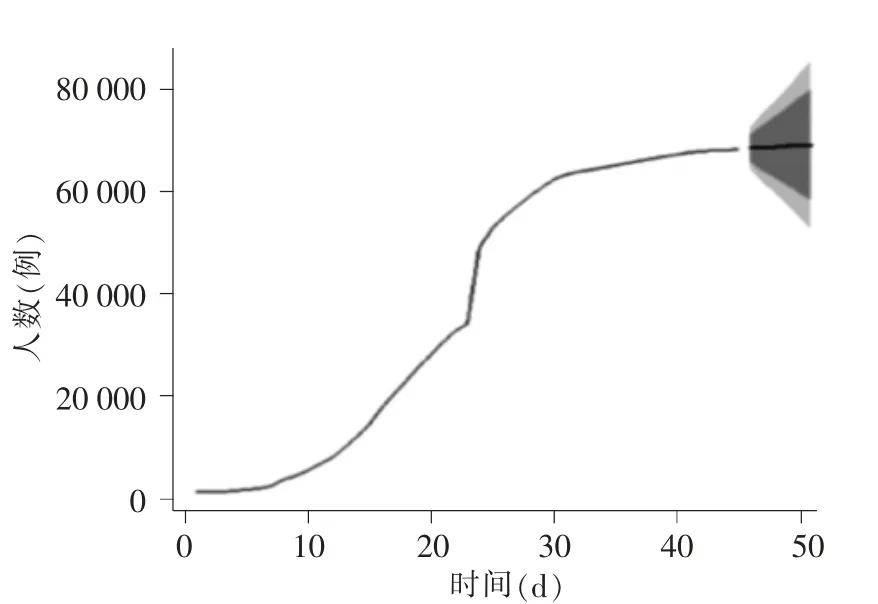
图4 预测图

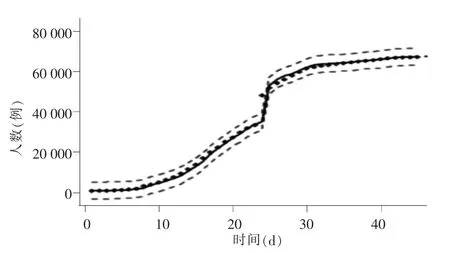
图5 个性化预测图

4 讨论与结论

4.1 数据结果

由以上数据可知，湖北省新冠肺炎确诊人数虽仍存在上涨趋势，但增长幅度已经明显减缓，说明我国采取的防疫措施十分有效。相信最终湖北省新冠肺炎确诊人数的增长幅度将减缓为零，确诊人数也将最终在某一数值保持不再增长。因此，继续坚持现有的相关防疫措施及政策，人们必将打赢这场防疫阻击战。

4.2 结论

本文综合运用ARIMA、趋势拟合等手段，完成相关建模与分析，短期预测效果突出，便于操作。在建模的过程中，坚持从数据本身出发寻找合适的模型，从而保证模型与数据之间具有较好的拟合效果，为后续的统计分析提供了便利，也保证了模型的可靠性。