广西壮族自治区艾滋病模型及预测分析

2020-05-18王楚雯

质量安全与检验检测 2020年2期

王楚雯胡颖侯颖

（大连民族大学理学院辽宁大连 116600）

1 前言

艾滋病是一种危害性极大的传染病，是由人免疫缺陷病毒（HIV）引起的慢性传染病。它把人体免疫系统中最重要的CD4T 淋巴细胞作为主要攻击目标，大量破坏该细胞，使人体丧失免疫功能。因此，人体易于感染各种慢性疾病，引发并发症，并可导致恶性肿瘤，病死率较高[1-3]。本病主要通过性接触、血液及母婴传播。

广西是多民族的聚居地，其中汉族和壮族是主要人口。这一地区自然增长率达到8.16%，人口增长较快，人口流动性也大幅增加。艾滋病具有传播迅速、发病缓慢、病死率高的特点，且无法根治，所以对艾滋病的预测、防控就显得尤为重要[4]。本文利用2013 年1 月—2019 年10 月广西壮族自治区艾滋病确诊与死亡数的月度数据，经数据处理、模型识别、模型优化等时间序列分析程序，找到拟合度最优的模型，进行5 期的预测与分析，并提出防控建议。

2 资料与方法

2.1 数据资料

数据来源于广西壮族自治区疾病预防控制中心[5]。从该网站公布的数据中收集了2013 年1 月—2019 年10 月广西省艾滋病确诊数与死亡数、死亡率的月度数据。

2.2 分析方法

艾滋病是一种传染性的疾病，其数据是典型的时序数据。本文首先对其进行描述性时序分析，其次，运用R 语言做出更为精准细致的统计时间序列分析。

本文构造自回归求和移动平均模式（ARIMA）模型，实质上是差分运算与ARMA 模型的结合，旨在将序列通过一阶或多阶差分后能够达到平稳，方能使用ARMA 模型进行拟合、预测。

具有如下结构的模型称为求和自回归移动平均模型，简称为 ARIMA（p，d，q）模型

其中，非负整数 d—求和阶数；Φ（B）=1-φ1B-……-φPBP—平稳可逆 ARMA（p，q）模型的自回归系数多项式；Θ （B）=1-φ1B-……-φqBq—平稳可逆 ARMA模型的移动平均系数多项式；d—阶差分算子。

▽d=（1-B）d=（-B）kARIMA 模型建立的过程如下：

进行平稳性检验进行白噪声检验-对ARIMA模型定阶-对定阶后的模型做残差检验-模型优化-模型预测，在建模过程中，使用R 语言。

3 数据结果

3.1 数据预处理

在原数据中缺失 2015年3月、2015年4月、2016年5月、2017年5月和2017年11月的数据。为此，采用样条插值法，将缺失的数据补全。将广西艾滋病的确诊数和死亡数的月度数据时序化，并绘制时序图（图1）。

由图1 可知，广西艾滋病发病数具有随机性趋势，没有在某一值上下波动，由此看出发病数具有非平稳性特征。广西艾滋病死亡率具有线性增加的趋势。

图1 时序图

3.2 数据平稳化

死亡率线性拟合趋势详见图2。

图2 死亡率线性拟合趋势

It为随机波动项，经白噪声检验It不是白噪声，但It似乎具有一定的规律性，在每年年末至第二年初死亡率达到峰值。为了对死亡率进行预测，根据经验对It进行一阶差分，结果发现，It与阶差分时间序列具有平稳特征。死亡率残差与残差分布详见图3。对差分后的It进行白噪声检验发现P＜0.05，即差分后的It为非白噪声序列。

对广西艾滋病发病数进行一阶差分后，发现可消除数据的随机性趋势，艾滋病1 阶差分后的数据具有明显的平稳特征，详见图4。通过对广西艾滋病差分数据进行白噪声检验发现P 值小于0.05，说明在95%的置信水平下拒绝了原假设，因此，有理由认为备择假设成立，即发病数差分序列为非白噪声序列。

3.3 模型识别

广西艾滋病发病数自相关及偏自相关图详见图5，广西艾滋病死亡率自相关及偏自相关图详见图6。由图5 可知，艾滋病发病数自相关具有一阶拖尾性，偏自相关图具有二阶拖尾性。因此艾滋病发病数预测模型为 ARIMA（2，1，2）。为了防止主观选取模型对预测模型造成误差，故根据图5 从不同的角度选取了多个备选模型。提供备选识别模型为：ARIMA（2，1，1）、ARIMA（1，1，1）和 ARIMA（1，1，2）。由图6可知，艾滋病死亡率It的一阶差分序列的自相关和偏自相关都表现为拖尾。根据拖尾特征，将It模型识别ARIMA（2，1，1）、ARIMA（1，1，1）和 ARIMA（3，1，1）。但由于艾滋病死亡率偏自相关函数拖尾结果并不明显，故同时对It进行自动定阶并建模，识别结果为ARIMA（1，0，0）、ARIMA（0，1，1）。

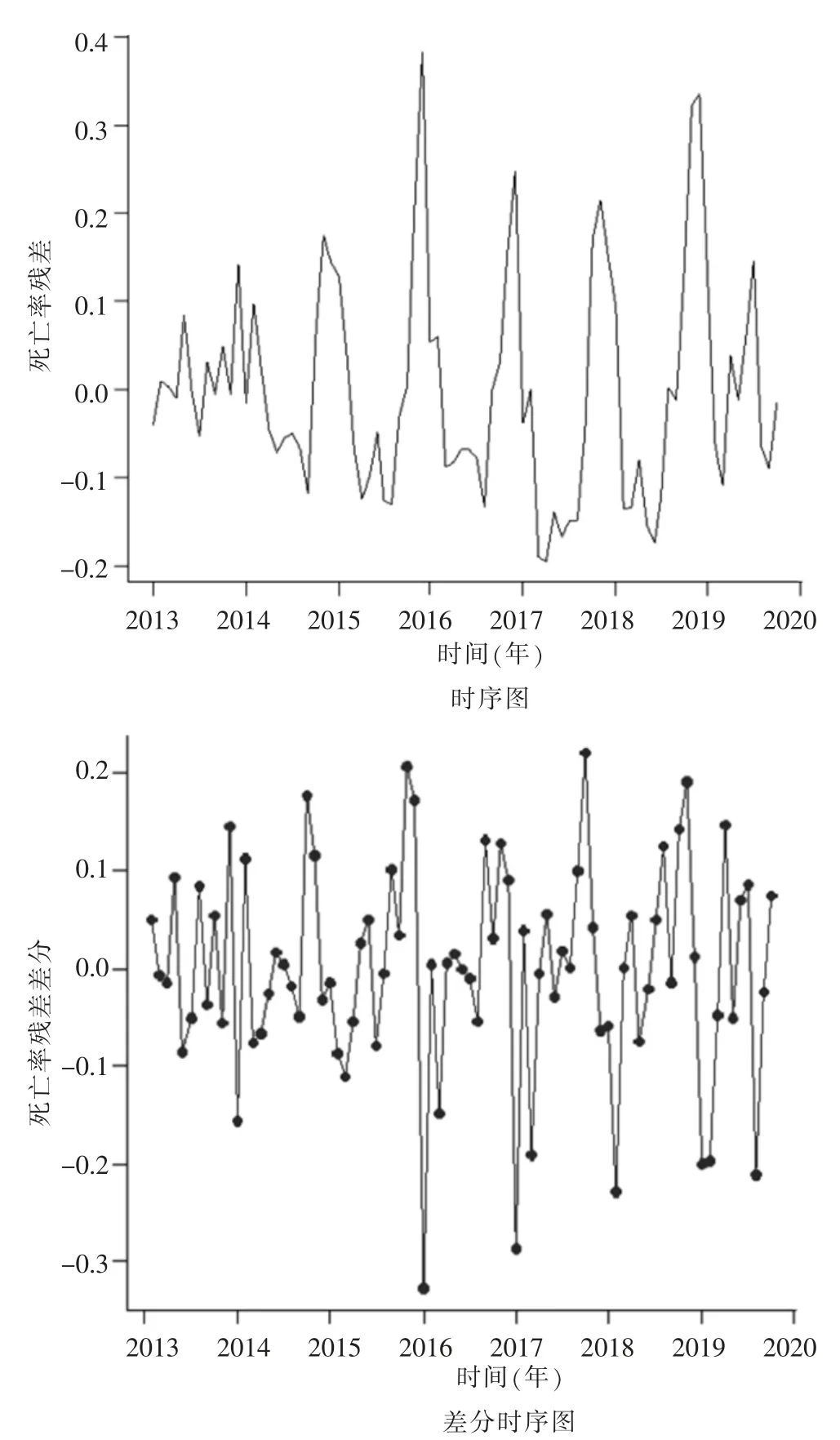
图3 It 时序图与差分时序图

图4 发病数差分时序图

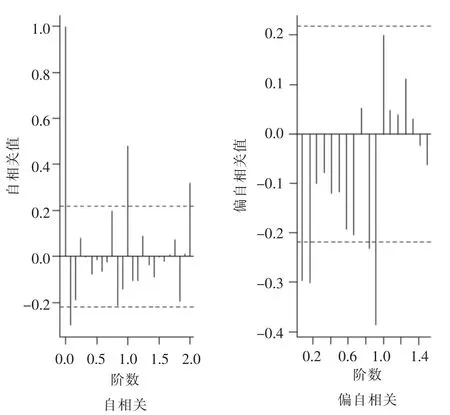
图5 艾滋病差分发病数自相关及偏自相关图

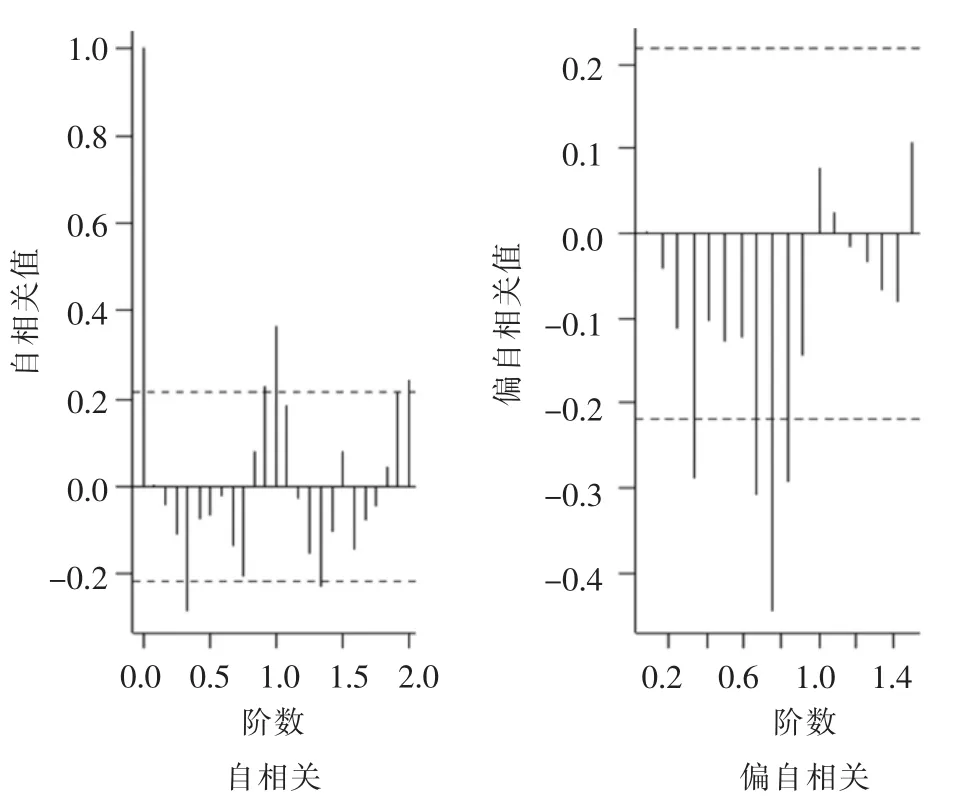
图6 It 差分自相关及偏自相关图

3.4 参数估计、模型检验和优化

（1）艾滋病发病数：对发病数所选定的4 个模型进行“最小二乘-极大似然”口径拟合，并对残差进行白噪声检验，P 值均大于0.05，认为模型都通过了检验。R 语言给出的参数估计都具有显著性，所以省去参数的显著性检验。观察通过检验模型的信息量，发现ARIMA（2，1，2）拟合发病数数据后所得的信息量 AIC=987.14，AICc=987.94，BIC=999.11，是所有拟合模型中最小的，故用模型 ARIMA（2，1，2）建模。模型如下：

（2）艾滋病死亡率：同理，使用类似于（1）的方法，得到最优模型为 ARIMA（2，1，1），模型如下：

▽It=0.769 2▽It-1-0.223 9It-2+εt+εt-1，

εt：WN（0，0.009 263）

3.5 模型建立

（1）广西艾滋病发病数模型

εt：WN（0，10 187）

（2）广西艾滋病死亡率模型

3.6 预测

使用建立的模型进行5 期预测，给出预测的80%和95%的置信区间，并绘制预测图。

广西艾滋病发病数预测结果详见图7，死亡率预测结果详见图8。

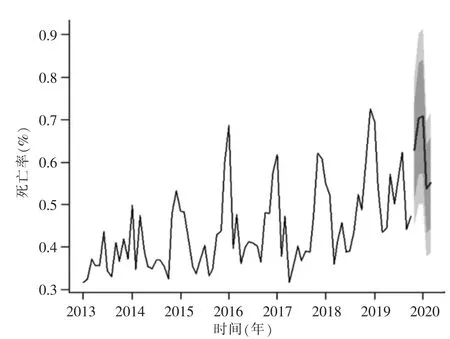
图8 艾滋病死亡率预测图

4 结论

以上数据表明，广西在2013—2019 年艾滋病确诊人数的数据处于较为平稳的状态，并没有出现明显增加或明显减少的情况。在对广西省确诊数据进行预测后发现，未来5 个月广西艾滋病确诊人数的数据处于下降状态，一定程度上说明了广西在艾滋病的防控上取得了较好的成果。另一方面，在对广西艾滋病死亡率拟合后发现，近年来广西艾滋病死亡率逐年上升。在对广西死亡率数据预测的过程中也发现死亡率处于先上升后下降的状态，但从总体上看死亡率还是处于上升的状态。通过查阅相关资料发现，艾滋病死亡原因主要为艾滋病相关死亡、艾滋病无相关死亡、意外死亡和自杀死亡[6]。鉴于艾滋病死亡的复杂性，排除了意外死亡病例后，与死亡相关的因素包括文化程度、家庭情况、酗酒、抗病毒治疗等。本文对广西2013—2019 年艾滋病死亡率进行调查，认为广西的文化程度、家庭情况、酗酒等因素不足以促使艾滋病死亡率增加。这说明广西当地的抗病毒治疗不利是艾滋病患者死亡率增加的主要原因。

通过观察死亡率残差的时序图发现，2013—2019 年期间每一年年末至第二年年初是艾滋病死亡的高发期。这说明，在春节期间艾滋病的死亡率明显增加，春节期间由于酗酒等因素导致非意外死亡中伴有其他慢性疾病病例的增加。因此，在春节期间，艾滋病患者在积极进行艾滋病抗病毒治疗的同时，也应注意与艾滋病无关的疾病的防治。