地铁线路轨距对轮轨接触行为的影响
2020-05-18陈嵘温静于浩安博洋徐井芒王平
陈嵘,温静,于浩,安博洋,徐井芒,王平
(1.西南交通大学高速铁路线路工程教育部重点实验室,四川成都,610031;2.西南交通大学土木工程学院,四川成都,610031)
轨距是钢轨踏面下16 mm 范围内两股钢轨工作边之间的最小距离,是保证列车运行安全的重要轨道几何距离,我国现运营铁路及城市轨道交通标准轨距为1 435 mm[1]。轨距对轮轨接触几何性能、车辆动力学性能、轮轨滚动接触行为、轮轨磨耗及滚动接触疲劳性能等都有显著影响[2-4]。曹文战等[5]提出根据机车-轨道系统动力学模型,建立轮轨接触模型和踏面磨耗模型为一体的机车车轮磨耗仿真模型,并编制数值计算程序,发现在一定程度上加宽轨距能减轻车轮的磨耗。蔡小培等[6]以18 号高速道岔为例,建立列车/轨道耦合动力学模型,仿真分析转辙器轨距加宽对尖轨道岔动力特性的影响。VINEESH 等[7-8]针对印度铁路总公司的车轮轮背内侧距增加进行调查分析,建立轮轴二维有限元模型,研究车辆制动、制动负载和车轮轮廓等对轮背内侧距演化的影响,发现车轮在制动过程中轮背距减小;当车轮温度冷却到常温时,轮背距增加,且更高的制动不均匀性引起车轮过热,将会导致轮距加宽。王文健等[9-10]分析轨底坡和轨距等参数对JM3 磨耗型车轮踏面与60 kg/m 钢轨匹配时轮轨接触几何和接触应力的变化,发现增加轨距对轮轨接触几何和蠕滑率产生较大影响,并可降低轮轨接触应力。张文军等[11]发现机务折返线平面设计中轨距与其主要运行机车的状态不匹配,导致轨距难以保持,提出针对不同曲线半径,轨距需要加宽。胡燚斌等[12]建立多自由度悬挂式单轨列车系统动力学模型,研究了不同轨距下悬挂式单轨列车的曲线通过能力,建议悬挂式单轨交通系统的合理轨距为784~788 mm。李克飞等[13]分析了轨道参数对曲线钢轨波磨的影响,发现加宽曲线段轨距可缓解既有线曲线钢轨波磨。综上所述,轨距加宽在一定程度上能改善轮轨匹配关系,缓减轮轨磨耗。由于受城市建设状况及工程地形条件等多因素的限制,地铁线路设计中,常不可避免地选择小半径曲线[14]。曲线半径越小,对钢轨的磨耗就越严重,缩短钢轨更换周期,导致运营费用增加[15]。因此,有必要分析轨距对地铁线路轮轨接触特性的影响规律,为我国合理选择地铁线路轨距参数、综合治理地铁线路轮轨磨耗及滚动接触疲劳问题提供理论支持。本文首先通过接触几何算法计算出不同轨距下LM车轮踏面与CHN60 钢轨滚动接触的接触几何参数;然后,利用Kalker 三维非Hertz 弹性体滚动接触理论及其数值程序CONTACT,根据Bossinesq-Cerruti力/位移公式和Gauss数值积分方法,计算轮轨滚动接触应力随轨距变化。
1 轮轨滚动接触计算模型
1.1 轮轨接触几何计算模型
利用迹线法基本原理编制轮轨接触几何算法程序。首先,通过辅助工具CAD 计算得出轮轨外形上各点的坐标,然后,利用三次样条函数拟合出轮轨外形,利用迹线法中2个几何条件:1)轮轨接触点处车轮和钢轨的垂向距离为零,非接触点处轮轨表面的垂向距离大于零;2)轮轨接触点处轮轨的轮廓线具有相同的斜率,即具有公切线,并根据第1个条件确定轮轨的接触点,再用第2个条件加以验证,便可求出轮轨接触点的位置。计算时使轮对由对中位置以0.5 mm 为计算步长向右横移12 mm,不考虑轮对的摇头角。具体计算参数如下:车轮名义滚动圆半径为420 mm,轮对内侧距为1 353 mm。计算在1 433,1 435,1 437 和1 439 mm这4种轨距状态下轮对接触点、滚动圆半径和接触角等接触几何参数,具体算法过程见文献[16-17]。
1.2 轮轨滚动接触蠕滑率计算
在确定轮轨滚动接触几何参数后,利用所得结果计算轮轨接触斑的蠕滑率。考虑平直轨道,忽略轮对绕轴线转动的干扰项β̇、车轮超前和滞后角αl,r及高阶小量对蠕滑的影响,得到蠕滑率计算公式[17-18]。计算时不考虑轮对的摇头角,忽略̇的影响。
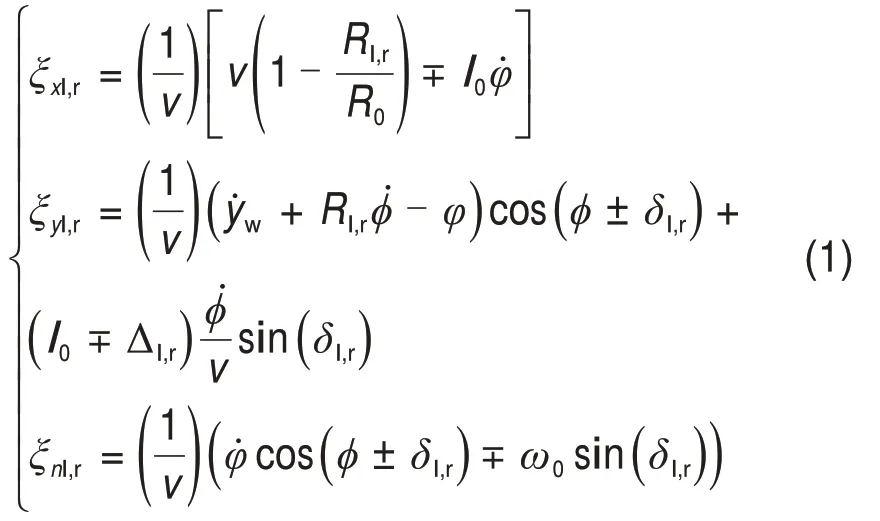
式中:ξxl,r,ξyl,r和ξnl,r分别为轮轨纵向、横向以及自旋蠕滑率;l和r分别对应左侧和右侧钢轨;v为车轮的名义速度;R0和Rl,r分别为轮轨接触名义滚动圆半径和瞬时滚动圆半径;l0为轮对处于轨道中央位置初始滚动圆到轮心的距离;δl,r,φ和φ分别为接触角、摇头角和侧滚角;,̇和̇分别为轮对横移速度、侧滚速度和摇头速度;ω0为名义滚动角速度,ω0=v/R0;Δl,r为接触点在车轮踏面上的横移量。
1.3 轮轨滚动接触力学模型
本文利用Kalker 三维非Hertz 弹性体滚动接触理论及其数值程序CONTACT 求解轮轨滚动接触。该程序将三维接触问题转化为1个离散的数学规划问题,利用Bossinesq-Cerruti力/位移公式,得到其离散形式为[17,19]

式中:PIi为元素I沿i方向上的表面牵引力;I和J为离散化中的元素数;i,j,z和τ为坐标方向;Q为所有元素的集合;Cτ为发生接触的元素集(PIz>0);AIiJj为影响矩阵,表示单元J上作用在j轴方向的单位表面牵引力引起单元I中心处沿i方向发生的位移;hI为元素I在z方向上的未变形距离;WIτ为 在元素I处的刚性位移;μ'Iτ为元素I沿τ方向上的初始位移;gI为单元I处的切向牵引界,依赖于法向压力PIz,局部位移SIτ=WIτ+μIτ-μ'Iτ。
2 结果与讨论
计算中轮对向右侧横移即右轨侧方向,本文中的轮轨接触几何和接触应力分析等均为右侧轮轨接触计算结果。
2.1 轮轨接触几何
轮轨几何接触是解释轮轨接触关系的基础。当轮对中心较轨道中心偏移较大时会发生轮缘接触,引起车轮踏面异常磨耗,恶化轮轨接触关系。
轮对接触点对分布对轮轨疲劳伤损的横向分布具有重要的影响,分布过于集中会引起轮轨疲劳伤损集中,缩短车轮及钢轨的使用寿命[20]。不同轨距下LM 车轮型面与CHN60 钢轨匹配时的轮轨接触点、滚动圆半径和接触角分布特征如图1 所示。由图1(a)可见:轨距变化下轮轨接触点存在明显差异;在相同横移量下,随着轨距加宽,接触点越偏向轨顶位置。如当横移量为6 mm时,标准轨距下接触点在钢轨上横向729.32 mm位置处,轨距1 439 mm 下接触点在钢轨上横向739.75 mm 位置处,向钢轨中心移动10.43 mm;6~9 mm 横移量范围的轮轨接触点在钢轨上的位置主要集中在轨顶R=80 mm 圆弧段。从图1 中可以看出:在6~9 mm横移范围内,随着轨距增大,接触点在钢轨横向分布范围变宽且明显偏向轨顶中心位置,有效避免局部伤损现象。
当轨距变化时,轮轨间的距离固定,轮轨接触点的接触位置随着发生变化,造成轮轨间不同位置的接触,从而改变车轮的滚动半径,如图1(b)所示;当横移量大于2 mm时,不同轨距下轮轨接触滚动圆半径开始产生差异,在相同横移量下,轨距越宽,滚动圆半径越小。由图1(b)可见:当横移量达到某一值时,滚动圆半径迅速增大,轮缘与钢轨侧面发生贴靠,而轨距增大,明显可以增大了滚动圆半径突增的横移值。
由图1(c)可见:轮对中心相对轨道中心线偏移达到2 mm后,轨距加宽导致同一横移量下轮轨接触角减小;与滚动圆变化规律相似,当横移量达到某一值时,轮轨接触角会发生剧增,轮缘与钢轨侧面会发生贴靠。标准轨距1 435 mm 情况下横移值为8.5 mm,轨距加宽至1 437 mm和1 439 mm后横移值分别为9.5 mm 和10.5 mm,可以看出轨距增加导致轮缘不易产生贴靠。
2.2 轮轨接触力学特性
此处以轮对横移量7 mm 的结果为例进行分析。计算中轮对摇头角为0,摩擦因数为0.4,垂向力为70 kN。
图2、图3 和图4 分别为不同轨距下轮轨接触斑黏滑分布、轮轨接触斑内正应力和切应力分布,对应各应力最大值及接触斑面积如表1所示。

图1 不同轨距下轮轨接触点、滚动圆半径和接触角分布特征Fig.1 Contact point,rolling radius and contact angle distribution under different gauges

图2 不同轨距下轮轨接触斑内黏滑分布Fig.2 Stick-slip distribution in wheel-rail contact patch under different gauges

图3 不同轨距下轮轨接触斑内正应力分布Fig.3 Normal stress distribution in wheel-rail contact patch under different gauges

图4 不同轨距下轮轨接触斑内切应力分布Fig.4 Shear stress distribution in wheel-rail contact patch under different gauges

表1 轮轨接触斑内正应力、切应力和接触斑面积最大值Table 1 The maximum value of normal stress,shear stress and area in wheel-rail contact patch
图2 中黄色区域为滑动区,蓝色区域为黏着区。从图2 可见:轨距变窄为1 433 mm 的轮轨接触斑在横向分布范围变窄,纵向范围变宽,接触斑面积减小27%,且整个接触斑均为滑动区,无黏着区存在,从而增加了轮轨的滑动行为,导致轮轨接触光带的宽度变窄,引起轮轨接触应力增加;当轨距加宽至1 437 mm和1 439 mm时,接触斑面积分别增大44%和77%,且轨距加宽至1 437 mm后接触斑开始出现黏着区,加宽至1 439 mm 时接触斑内黏着区面积显著增大,减小了轮轨的滑动行为。
由图3和图4可见:轨距变化对轮轨接触斑内正应力和切应力分布有明显影响。轨距变窄为1 433 mm,轮轨接触斑最大正应力及切应力变大,均增加17%;轨距加宽至1 437 mm 和1 439 mm时,显著降低正应力及切应力,其中正应力分别降低31.38%和64.70%,切应力分别降低31.38%和64.70%,这将有效减轻轮轨间疲劳伤损。
不同轨距下轮轨接触斑内Mises等效应力分布差距较大。图5 所示为轮轨体内沿纵向和深度(XZ)平面内的等效应力分布。轨距自1 433~1 439 mm之间变化,轮轨体内最大等效应力减小,且沿纵向分布范围变宽,沿深度方向影响范围增大,可避免等效应力的集中作用。标准轨距下轮轨体内等效应力最大值为2 097 MPa,轨距加宽2 mm 和4 mm 后,轮轨体内等效应力最大值分别为1 381 和922 MPa,显著减小等效应力,分别降低34%和56%。

图5 不同轨距下轮轨接触斑内等效应力分布Fig.5 Equivalent stress distribution in wheel-rail contact patch under different gauges
图6 所示为不同轨距下等效应力沿深度(Z)方向变化。由图6 可见:轨距在1 437~1 439 mm 之间变化的等效应力最大值均发生在轮轨接触表面,其中轨距加宽至1 437 mm和1 439 mm的等效应力在深度1~3 mm内出现峰值;当深度超过3 mm后,随着深度增加等效应力迅速下降,在深度达到10 mm 以后基本重合,在10 mm 深度之内,在同一深度处轨距加宽等效应力减小;当横移量较大时,轮轨接触点偏离轨顶中心线较远,易产生较大的接触应力,钢轨在接触力的作用下会变形,且在接触斑附近数值较大,容易导致轮轨超过普通碳钢(Q235)的接触疲劳极限422 MPa[21],产生塑性变形,引发材料的接触疲劳损伤。等效应力减小可减轻轮轨材料从表面到深度领域内的疲劳破坏。
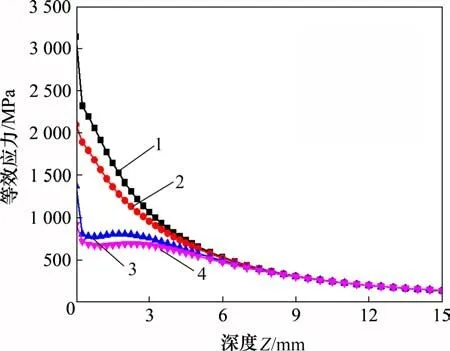
图6 不同轨距下等效应力随深度变化曲线Fig.6 Equivalent stress varies with depth under different gauges
3 结论
1)轨距加宽导致同一横移量下接触点越偏向钢轨中心位置。在6~9 mm 横移范围内,轨距加宽导致接触点分布范围变宽且偏向轨顶中心。轨距加宽引起轮轨滚动圆半径和接触角减小,增大了滚动圆半径和接触角剧增的横移量,导致得轮缘不易产生贴靠,有效避免局部伤损。
2)与标准轨距相比,轨距变窄导致轮轨接触斑在横向的分布范围变窄,纵向分布范围变宽,接触斑面积减小;轨距加宽至1 437 mm 后接触斑开始出现黏着区,加宽至1 439 mm 时接触斑内黏着区面积显著增大,其接触斑面积增大77%,减小轮轨的滑动行为。
3)轨距在1 433~1 439 mm之间变化,轮轨接触斑内正应力和切应力显著降低,轮轨体内最大等效应力显著减小,且沿纵向分布范围变宽,沿深度方向影响范围增大,可避免等效应力的集中作用,减轻轮轨材料从表面到深度领域内的疲劳破坏。
4)轨距加宽有利于地铁线路轮轨关系的匹配,降低轮轨间接触应力,减轻轮轨间的磨耗和疲劳伤损,针对不同曲线半径,轨距具体加宽设置值在后续工作中有待进一步深入研究。
