基于单元建模法的怠速工况传动系建模及多种扭转减振器性能对比
2020-05-18陈龙史文库陈志勇
陈龙,史文库,陈志勇
(吉林大学汽车仿真与控制国家重点实验室,吉林长春,130022)
汽车传动系是一个非常复杂的多自由度非线性系统,发动机输出扭矩的不平稳使传动系产生一系列的振动噪声问题,影响车辆NVH 性能。此外,扭转振动还会使系统部件承受较大的扭转载荷,在花键、齿轮等传动间隙处出现敲击现象,从而降低传动系零部件性能、减少使用寿命,增加车辆的燃油消耗[1-2]。因此针对车辆传动系精确建模、性能仿真及减振方法研究尤为重要。目前针对传动系仿真建模研究较多,宋立权等[3]采用单元分析法建立车辆传动系,并对双质量飞轮扭转减振器减振性能进行仿真分析,模型没有考虑扭转减振器和变速器齿轮非线性问题,且没有进行试验验证;吴虎威等[4-5]分别针对装有离合器扭转减振器的变速箱敲齿问题进行建模仿真,仿真结果与试验结果一致性较好,但是在变速箱啮合齿轮对啮合刚度建模时,没有考虑斜齿圆柱齿轮的时变啮合刚度问题;刘雪莱等[6-7]针对装有离合器减振器的传动系怠速工况敲齿问题进行动力学分析,并对减振器进行优化,在对发动机动态扭矩建模时采用正弦函数拟合的方法,未考虑发动机摩擦力矩等因素对输出力矩的影响;YOON 等[8-9]建立WOT工况下整车传动系模型,分析离合器扭转减振器和双质量飞轮结构参数对变速器敲齿的影响;IDEHARA 等[10]建立了三自由度传动系模型,分析了离合器参数对传动系扭振影响,但是上述研究对传动系中发动机和变速箱啮合齿轮对建模考虑较为简单,精度较低。在此,本文作者综合考虑发动机、扭转减振器以及变速箱存在的非线性因素,建立更精确的怠速工况传动系模型;并对模型进行试验验证;同时对离合器扭转减振器、双质量飞轮扭转减振器以及一种新型离心摆式双质量飞轮扭转减振器进行非线性建模;基于本文所建的怠速工况传动系模型,分别对3种扭转减振器进行对比分析。
1 怠速工况传动系模型
怠速工况传动系扭振模型如图1 所示,图中,J1为双质量飞轮第一质量转动惯量;J2为双质量飞轮第二质量转动惯量;J3为离合器、变速器输入轴及主动齿轮总的转动惯量;J4为从动齿轮转动惯量;θ1,θ2,θ3和θ4分别为双质量飞轮第一质量、第二质量、变速器主动齿轮和变速器从动齿轮角位移;Tengine为发动机输出扭矩;Tdamper为扭转减振器传递的扭矩;ks和cs分别为变速器输入轴扭转刚度和阻尼;Fgear为变速器齿轮啮合力;Ra和Rp分别为主动齿轮和从动齿轮节圆半径;Tdrag为变速器齿轮转动过程受到的阻力矩。
根据牛顿第二定律,图1所建立的四自由度动力学模型数学方程为

采用单元模块化思想,分析传动系模型及动力学方程可知四自由度传动系模型可分为发动机输出扭矩模型、非线性扭转减振器模型以及变速箱啮合齿轮对模型。
1.1 准瞬态发动机模型
传动系扭振问题主要由发动机输出扭矩波动引起,因此,在对扭振问题进行建模分析时必须考虑发动机的扭矩波动。准瞬态发动机模型[10-11]是以发动机缸压曲线作为输入计算得到发动机的动态输出,能够有效反映发动机输出扭矩的动态特性,满足分析扭振问题的要求。根据发动机单缸曲柄连杆机构的运动学关系得到发动机输出惯性力矩和燃烧产生的气体力矩,通过多缸发动机曲轴曲柄相位角得到多缸发动机输出扭矩,同时考虑摩擦对发动机输出扭矩的影响。

图1 怠速工况传动系扭振模型示意图Fig.1 Schematic diagram of torsional vibration model of idle speed transmission system
1.1.1 单缸发动机扭矩模型
发动机曲柄连杆机构是由活塞、连杆和曲轴等部件组成的复杂系统,其结构运动简图如图2所示,图中:α为曲轴转角;β为连杆摆动角度;r为曲柄半径;L为连杆长度;mp为活塞、活塞环、活塞销及连杆部分长度的等效质量;Fg为缸内压强在活塞端面产生的正压力。
由图2中的运动学关系可得曲轴转角与活塞位移的关系为
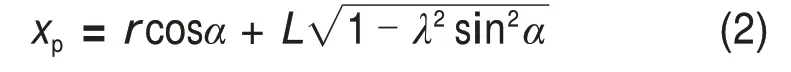
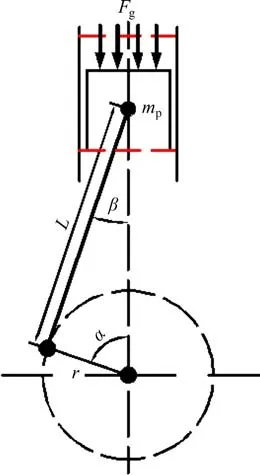
图2 发动机曲柄连杆机构运动关系图Fig.2 Engine crank linkage mechanism motion diagram
式中:λ=r/L。
根据文献[3],式(2)中根号部分可按级数近似展开,取前2项为

设曲轴角速度为ω,则:

根据式(3)和式(4)可得往复惯性力为
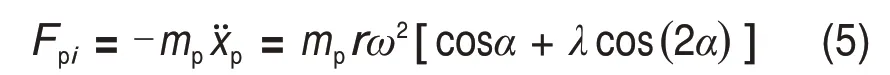
式中:Fpi为第i个气缸产生的往复惯性力。
发动机缸内燃烧压力产生的气体力为

式中:Fgi为第i个气缸产生的气体作用力;D为活塞直径;Pgas为发动机缸压。
发动机往复惯性力和气体作用力在曲轴产生的扭矩计算公式为:

式中,TPi为第i个气缸产生的惯性力矩;Tgi为第i个气缸产生的气体力矩。
怠速工况下发动机缸压曲线实测值如图3 所示。根据实测所得缸压曲线以及式(7)和式(8)计算得到怠速工况下单缸产生的惯性力矩和气体力矩如图4所示。
1.1.2 单缸发动机摩擦模型
发动机摩擦模型本文采用RH模型[4,13],该模型将摩擦力矩分为多个系统结构的摩擦力矩。
活塞环黏性摩擦力矩为

式中:

图3 怠速工况缸压曲线Fig.3 Idle pressure cylinder pressure curve

图4 单缸发动机力矩Fig.4 Torque curve of single-cylinder engine

活塞环混合摩擦力矩为

活塞裙部摩擦力矩为

气门组摩擦力矩为

附件摩擦力矩为

主轴承摩擦力矩为

综上可得发动机单缸总摩擦力矩为

式中:μ为润滑油动力黏度;Pr为活塞环与缸壁压力;ω0为油环厚度;d为气缸内壁直径;n0为油环个数;nc为气环个数;ωc为气环厚度;h0为润滑油膜厚度;Ls为活塞裙部长度;nv为单气缸气门个数;Fs为气门弹簧力;rjb为轴承平均半径;ci(i=1,2,…,6)为发动机摩擦力矩系数。
1.1.3 四缸汽油发动机模型
式(7)~(16)可得发动机各缸输出扭矩,根据四缸发动机相位角关系,发动机输出扭矩为

发动机参数如表1所示。
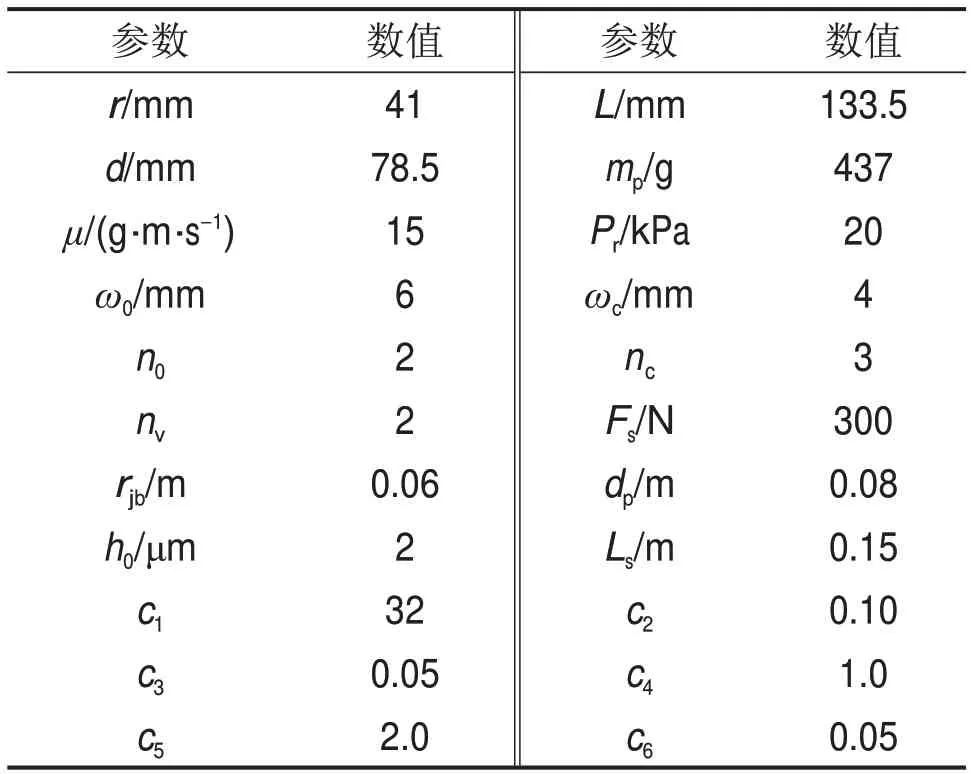
表1 发动机模型参数Table 1 Parameters of engine model
由表1可得发动机输出特性,考虑摩擦力矩与不考虑摩擦力矩的发动机输出扭矩对比曲线如图5所示。
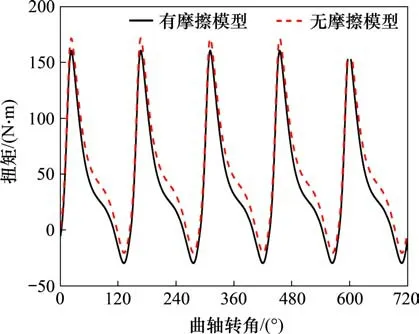
图5 发动机输出扭矩对比Fig.5 Comparison of engine output torque
由图5 可知:摩擦力矩对输出扭矩有一定影响,受摩擦力矩的影响,怠速工况下发动机输出扭矩比理想扭矩小。当高转速时,摩擦扭矩的影响更大,因此,考虑摩擦力矩更能反映发动机的动态输出。
1.2 传动系扭转减振器模型
车辆传动系扭转减振器目前主要有:离合器扭转减振器和双质量飞轮扭转减振器,同时本文还对新型离心摆式双质量飞轮(将离心摆和双质量飞轮集成)进行建模,然后对上述多种扭转减振器特性进行仿真分析。
1.2.1 离合器扭转减振器
本文研究的离合器扭转减振器为两级刚度,其扭转特性曲线为非线性,扭矩与扭转角度关系式[5]为

式中:kc1和kc2分别为离合器扭转减振器第一、二级扭转刚度;θc1和θc2分别为一级和二级扭转刚度转角极限值;H1和H2分别为一级、二级干摩擦阻尼;为平滑拟合函数,δ为拟合系数,本文取100。最终得到离合器扭转减振器扭转特性曲线如图6所示。
1.2.2 双质量飞轮扭转减振器

图6 离合器扭转减振器特性曲线Fig.6 Characteristic curve of clutch torsional damper
双质量飞轮是一种新型扭转减振器,本文采用两级刚度双质量飞轮,其扭转特性模型为:
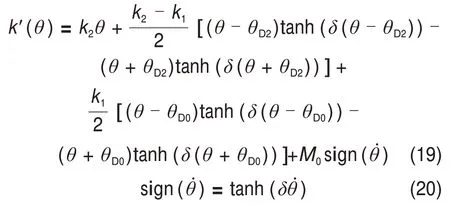
式中,θD0和θD2分别为双质量飞轮空行程转角和一级刚度极限转角;M0为双质量飞轮干摩擦阻尼。
双质量飞轮扭转特性曲线如图7 所示。由图7可知:双质量飞轮相对扭转角度比离合器扭转减振器大,扭转刚度比离合器的小,因此,其减振性能要比离合器的更好,且所建模型与试验曲线基本一致,表明本文所建模型满足仿真需求。

图7 双质量飞轮扭转减振器特性曲线Fig.7 Characteristic curves of DMF torsional damper
1.2.3 离心摆式双质量飞轮扭转减振器
离心摆式减振器是一种被动式动力调谐吸振器,最早应用于航空领域。为了进一步提升其减振性能,将离心摆与双质量飞轮扭转减振器结合形成复合型的离心摆式双质量飞轮,其结构原理如图8所示。
由图8可得其动力学方程为
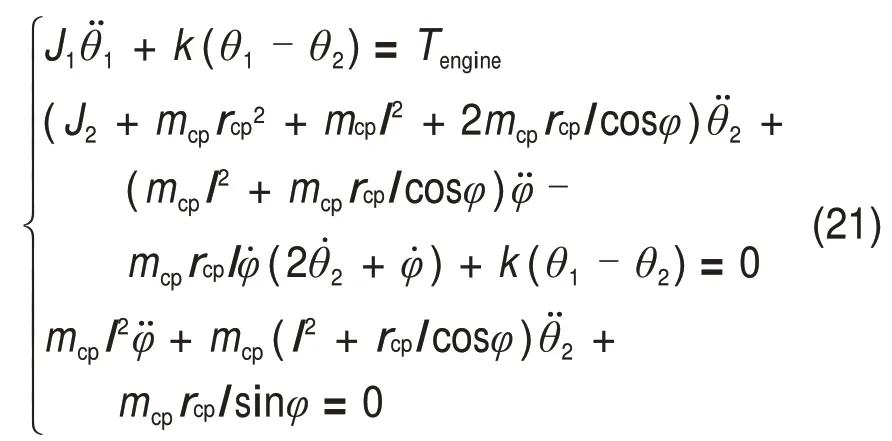

图8 离心摆式双质量飞轮结构图Fig.8 Centrifugal pendulum DMF structure
式中:mcp为离心摆总质量;φ为离心摆角位移;k为双质量飞轮扭转刚度;rcp为安装有离心摆的第二质量回转中心到离心摆摆动中心距离;l为离心摆摆动半径。
通过合理设计离心摆式减振器的半径比能有选择地吸收发动机主要阶次的振动,大幅度衰减发动机扭矩波动[14]。以四缸发动机为例,其主要阶次为发动机2阶激励,故本文离心摆式双质量飞轮调谐阶次设计值为

式中:n为离心摆调谐阶次。
1.3 考虑时变啮合刚度及齿间间隙的齿轮对建模
变速器啮合齿轮对的动力学简化模型如图9所示。
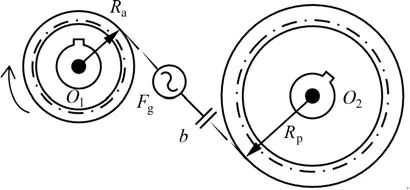
图9 单对啮合齿轮动力学模型Fig.9 Single pair meshing gear dynamics model
由图9可知:由于齿轮啮合间隙b的存在,齿轮对可能出现不接触,根据齿轮对间的相对位移,齿轮对间啮合力Fgear可表示为[6,15,16]

式中:δg和分别为相对角位移和相对角速度,为齿轮啮合刚度;b为单侧齿轮啮合间隙。
当|δg|≥b时,齿轮处于啮合状态;反之,当|δg| 式中:Requ为齿轮等效半径;a为齿顶高。 非承载自由旋转齿轮还会受到润滑油产生的搅油阻力矩,其计算公式[17-18]为: 式中:ρ和η0分别为润滑油密度和动力黏度;b0,h,ω和Sm分别为浸油齿轮宽度、浸油高度、齿轮转速和浸油表面积;Cm为搅油阻力矩系数;V为油体积;Fr为弗劳德数;Re为雷诺系数;g为重力加速度。 变速箱齿轮是斜齿圆柱齿轮,由于螺旋角的存在和重合度非整数,导致啮合过程中齿对数随着齿轮转动发生变化,因此齿轮的啮合刚度是时变的[19]。本文啮合刚度根据斜齿轮齿轮接触线的变化规律计算得到: 式中:k0为单位接触线长度啮合刚度;L(τ)为齿轮副瞬时总接触线长度。 单对齿轮接触线长度L0(τ)为 式中:pbt为端面分度圆齿距;B为齿宽;βb为基圆螺旋角;εγ=εα+εβ,为总重合度,εα和εβ分别为端面和轴面重合度;L2=Btanβb。 根据单对齿轮接触线长度可得整个啮合过程为: 根据公式计算得到时变刚度如图10所示。 图10 齿轮对时变啮合刚度Fig.10 Gear pair time-varying meshing stiffness 为了验证本文建立的怠速工况仿真模型的准确性,进行实车试验验证,由于试验条件限制,仅对装有双质量飞轮的动力学模型进行验证。分别采集怠速工况下双质量飞轮第一质量和第二质量的转速信号,仿真与试验所得的双质量飞轮转速波动如图11所示。 由图11 可知:仿真结果与试验结果一致,说明本文模型的正确性。同时分别对发动机有无摩擦模型仿真结果与试验结果进行对比可知,无摩擦模型发动机仿真结果振动幅值稍大,但是发动机有无摩擦模型二者差异较小,这是由于怠速工况下转速较低,摩擦阻尼力影响较小,有摩擦模型的仿真结果更好,因此,本文仿真分析都采用含有摩擦模型的发动机模型。 图11 双质量飞轮转速Fig.11 Rotational speed of double mass flywheel 发动机怠速转速在750 r/min 上下波动,第一质量转速波动幅值为20 r/min左右,第二质量转速波动幅值为10 r/min左右;试验结果与仿真结果时域转速曲线较为一致,只在波动峰值存在一定差异,但总体来看模型较为准确。发动机输出转速经过双质量飞轮扭转减振器后,其转速波动得到大幅度衰减,分别计算得到仿真与试验第一质量转速波动均方根分别为11.0 r/min 和9.6 r/min;第二质量转速波动均方根分别为5.4 r/min 和4.3 r/min,仿真与试验的转速波动衰减幅度分别为50.9%和55.2%,进一步说明仿真模型较为准确。 对有摩擦模型的仿真结果和试验转速信号进行频谱分析,结果如图12所示。由图12可知:转速信号2,4,6阶转速波动非常明显,仿真信号与试验信号基本一致,计算得到平均转速与各阶次幅值如表2所示。由表2可知:仿真信号与试验信号计算结果误差较小,满足本文后续仿真需求。 图12 转速信号频谱分析Fig.12 Analysis of speed signal spectrum 表2 转速仿真结果与试验结果对比Table 2 Comparison of simulation results and test results of rotational speed r/min 利用模型分别对离合器减振器、双质量飞轮扭转减振器和新型离心摆式双质量飞轮扭转减振器的减振性能进行对比分析。 离合器扭转减振器参数如表3所示。 安装离合器扭转减振器怠速工况下仿真结果如图13所示。 表3 离合器参数Table 3 Clutch parameter 图13 离合器扭转减振器响应曲线Fig.13 Response curves of clutch torsional vibration damper 仿真所使用的双质量飞轮扭转减振器参数如表4所示。安装双质量飞轮传动系怠速工况仿真结果如图14所示。 离心摆式双质量飞轮是在双质量飞轮基础上安装离心摆的复合型扭转减振器,在仿真过程中,双质量飞轮参数不变,离心摆的参数如表5 所示,仿真结果如图15所示。 表4 双质量飞轮参数Table 4 parameter of DMF 图14 双质量飞轮扭转减振器响应曲线Fig.14 DMF torsional vibration damper response curves 对比不同扭转减振器的减振性能可知,离合器减振性能较差,双质量飞轮次之,新型离心摆式双质量飞轮减振性能最好。分别计算安装各型减振器输入输出转速、角加速度波动均方根,结果如表6所示。 表5 离心摆参数Table 5 Parameters of centrifugal pendulum 图15 离心摆式双质量飞轮扭转减振器响应曲线Fig.15 Centrifugal pendulum DMF torsional vibration damper response curves 由表6可知:双质量飞轮和离心摆式双质量飞轮输入转速波动和角加速度波动相差不大,这是由于离心摆式双质量飞轮减振器只是在传统双质量飞轮次级质量上增加几组(通常为4 组)离心摆,对原双质量飞轮的第一质量无影响;安装离合器后,输入转速波动、角加速度波动变小是由于安装离合器扭转减振器时,发动机传统铸铁飞轮的转动惯量为0.17 kg·m2,比双质量飞轮转动惯量大,所以其输入转速波动小。对比可知,新型离心摆式双质量飞轮扭振衰减幅度最高达74.8%,安装离心摆后提升了传统双质量飞轮的减振性能,可进一步提升车辆NVH性能。 表6 减振器转速波动均方根Table 6 Damper speed fluctuation RMS 1)分别对发动机、扭转减振器、变速器常啮合齿轮对进行精确建模,考虑发动机动态扭矩波动,多种扭转减振器非线性模型、齿轮对啮合间隙、时变啮合刚度以及非承载齿轮转动过程受到的拖拽阻尼力矩等因素,建立发动机怠速工况四自由度模型,并对模型进行实车试验验证,仿真结果与试验对比表明:所建模型准确,满足工程应用需求。 2)分别对多种传动系扭转减振器进行建模,其中包括离合器扭转减振器、双质量飞轮以及新型离心摆式双质量飞轮扭转减振器,并基于怠速工况四自由度模型对3种扭转减振器的减振性能进行对比分析。仿真结果表明:安装离心摆能够进一步提升双质量飞轮的减振性能,新型离心摆式双质量飞轮减振器转速和角加速度波动衰减幅度达到70%以上,是一种性能优异的扭转减振装置,可进一步提升车辆NVH性能。


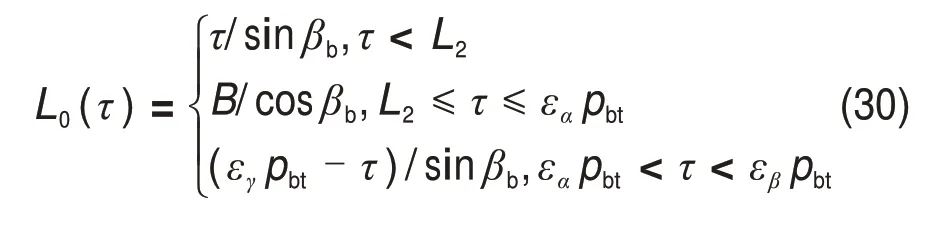


2 模型验证试验



3 减振器性能对比分析
3.1 离合器扭转减振器


3.2 双质量飞轮扭转减振器
3.3 离心摆式双质量飞轮扭转减振器





4 结论
