基于石墨烯复合薄膜的应变传感器及性能分析
2020-05-18卫军吴志强董荣珍
卫军,吴志强,董荣珍
(中南大学土木工程学院,湖南长沙,410075)
应变传感器是测量物体受力变形所产生的应变的一种功能型器件,在结构损伤探测和健康监测等方面有着广泛的应用[1-2]。传统的电阻式应变传感器主要是利用金属或半导体材料的压阻效应制备[3],其技术水平在过去几十年没能实现重大突破。传统应变传感器自身存在的缺陷(量程小、韧性差等)以及在复杂结构、大应变的监测等方面的应用越来越不能满足人们的需求,研制大量程、高灵敏、柔韧性好、可便捷使用的应变传感器十分必要。纳米材料独特的结构和性状可以增强和改性高分子聚合物,为制备新型应变传感器提供了理论基础[4-9]。然而,以纳米炭黑和碳纳米管为代表的导电填料的复合材料具有灵敏度低、填充量高、重复性不高等问题。近年来,具有优异力学和电学性能的二维纳米材料石墨烯成为国内外研究的热点[10-13],但大尺寸单层石墨烯拉伸程度有限(最大应变约为6%)[14],且制备工艺复杂,成本高,生产周期长,此外,石墨烯纳米粉末不易分散的性质也限制了其与聚合物复合[15-16]。纳米纤维素由于纤维尺寸达到纳米级,具有很多独特的性能[17-18],其能够在一些溶剂中形成均匀稳定的悬浮液,可以纳米纤维素为分散剂搭载石墨烯,从而形成均匀稳定的石墨烯-纳米纤维素悬浮液。纳米纤维素之间相互交叉搭接,使得石墨烯形成稳定的三维交联的多层次导电网络结构,同时,纳米纤维素具有良好的相容性,使石墨烯-纳米纤维素能与聚合物产生紧密的微观界面结合,这为石墨烯与聚合物复合提供了新的方法。本文作者以石墨烯为导电填料,借助纳米纤维素良好的分散性搭载石墨烯,采用溶剂挥发法在硅橡胶基底上形成多孔隙结构的石墨烯-纳米纤维素薄膜,并采用真空方法将硅橡胶嵌入薄膜孔隙中,制备具有层状结构的基于石墨烯复合薄膜的应变传感器,对石墨烯-纳米纤维素悬浮液分散性和石墨烯复合薄膜传感器的应变-电阻性能进行测试,分析传感器的应变-电阻响应机理,建立石墨烯复合薄膜的压阻行为预测理论模型。
1 实验
1.1 实验材料
石墨烯采用还原氧化石墨烯(rGO,纯度大于98%,厚度为1~3 nm,片层直径为0.5~5.0 μm,层数为3~5层,外观黑色蓬松粉末),购自苏州碳丰石墨烯科技有限公司;纳米纤维素(CNF,纯度大于99%,直径为4~10 nm,长度为1~3 μm),购自桂林奇宏科技有限公司;硅橡胶采用聚二甲基硅氧烷(PDMS,Sylgard 184),购自美国道康宁公司;异丙醇(AR,纯度>99.5%),购自上海麦克林生化科技有限公司。
1.2 rGO-CNF/PDMS薄膜传感器的制备
rGO-CNF/PDMS薄膜传感器的制备过程如图1所示。首先将一定质量比的rGO 与CNF 粉末溶于异丙醇中,经磁力搅拌后,再超声分散,得到rGO-CNF 悬浮液。将PDMS 与固化剂按质量比10꞉1混合均匀,经自然流平、真空脱气后,通过控制固化温度和时间,在其呈半固化状态时,将rGO-CNF 悬浮液涂敷于PDMS 表面。半固化状态的PDMS 已具备足够的支撑性和较强的黏性,有利于rGO-CNF 吸附于其上。在溶剂挥发的同时,PDMS 继续固化,悬浮液中的rGO-CNF 则黏贴堆积于PDMS表面,形成一层多孔结构薄膜。随后,在rGO-CNF 薄膜上涂敷一层PDMS,置于真空箱中固化,促进PDMS 进入薄膜孔隙中。固化完成后即形成rGO-CNF/PDMS薄膜。

图1 rGO-CNF/PDMS薄膜传感器制备流程示意图Fig.1 Schematic diagram of preparation process of rGOCNF/PDMS film sensor
2 实验结果与分析
2.1 rGO-CNF悬浮液的分散性分析
CNF 由于表面存在大量羟基而呈现出较强的极性,并在制备CNF 的酸解过程中引入带负电荷的基团间排斥作用,使得CNF 能够在极性溶剂异丙醇中形成均匀稳定的悬浮液。rGO由于化学活性低和比表面积很高,在溶剂中常出现团聚或分散不均匀现象。而rGO 表面分布着部分未被还原的羟基和羧基基团,可以通过氢键结合的方式与CNF 表面的羟基相互作用,实现CNF 对rGO 的模板搭载作用,提高rGO 在异丙醇中的分散性。另外,CNF与rGO之间存在π-π作用,π体系间具有很强的吸引力。利用氢键作用、π-π作用、静电斥力等协同作用使得rGO-CNF 在异丙醇中实现稳定分散。

图2 rGO,CNF和rGO-CNF悬浮液的紫外-可见吸收光谱Fig.2 Ultraviolet-visible absorption spectra of rGO,CNF and rGO-CNF suspension
图2 所示为rGO,CNF 和rGO-CNF 悬浮液的紫外-可见吸收光谱图。从图2 可见:由于rGO 团聚在一起产生隧道效应,rGO 悬浮液在200~1 100 nm 光谱范围内没有吸收峰;CNF 悬浮液分散良好,出现了特征吸收峰;rGO 和CNF 的混合溶液在270 nm 附近也出现了特征吸收峰,但并不是rGO 和CNF 吸光度的叠加,说明这两者不是简单的物理混合,而是发生了化学作用,削弱了一些基团峰,但相互作用不明显。图3所示为rGO和rGO-CNF 悬浮液静置24 h 前后粒子悬浮状态对比图。从图3 可见:静置24 h 后,rGO 悬浮液由于rGO 碎片团聚,出现明显沉淀,而rGO-CNF 复合物悬浮液仍呈现出均匀分散的悬浮状态。图4所示为2 种悬浮液的电阻R随时间变化情况。从图4 可见:rGO 悬浮液的电阻随时间逐渐增大,而rGOCNF 悬浮液的电阻较稳定。以上现象均表明CNF能有效协助rGO分散,形成稳定的悬浮液。另外,CNF 之间彼此交错连接,易形成便于离子和电子传输的多孔结构。图5 所示为是否掺加CNF 所形成的2种薄膜的吸水能力对比。在2种薄膜上滴少量的去离子水,rGO-CNF薄膜上的水被快速吸收,而纯rGO 薄膜上的水很难浸入薄膜内,表明rGOCNF 薄膜存在很多孔隙结构,而rGO 薄膜较密实。
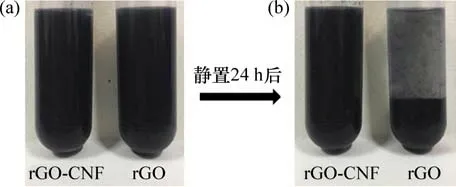
图3 rGO和rGO-CNF悬浮液静置前后粒子悬浮状态对比Fig.3 Comparison of particle suspension state of rGO and rGO-CNF suspension before and after static position

图4 rGO和rGO-CNF悬浮液电阻R与时间的关系Fig.4 Relationship between resistance variation of rGO and rGO-CNF suspension and time

图5 rGO-CNF和rGO薄膜的吸水能力对比Fig.5 Comparison of water adsorption of rGO-CNF and rGO films
2.2 rGO-CNF/PDMS传感器力电性能分析

图6 rGO-CNF和rGO-CNF/PDMS 薄膜拉伸能力对比Fig.6 Comparison of tensile property of rGO-CNF and rGO-CNF/PDMS films

图7 3种薄膜的相对电阻与应变的关系Fig.7 Relationship between relative resistance change and strain of three films
图6(a)所示为rGO-CNF 悬浮液经过滤干燥后得到的rGO-CNF 薄膜,其只能拉伸到非常有限的程度(最大应变约为5%),进一步拉伸时会断裂,其相对电阻变化与应变的关系曲线如图7所示。图7中,R0为初始电阻,ΔR为电阻变化量,ε为薄膜应变。应变传感特性不显著且拉伸范围有限,而rGO-CNF/PDMS 复合薄膜则可以拉伸至80%不发生破坏(如图6(d)所示)。PDMS 的嵌入显著提高了复合薄膜的拉伸性能。复合薄膜的拉伸能力主要取决于嵌入的弹性基体PDMS,而PDMS的拉伸极限取决于厚度。另外,可以选择不同弹性模量的基体嵌入rGO-CNF 薄膜中以制得可以满足不同测试需求的复合薄膜,XU 等[19]采用的共聚酯可以拉伸至300%。
一维纳米材料碳纳米管(CNT)也常用于制备具有应变传感性能复合材料的导电填料。从图7 可见:在应变为20%时,CNT 复合薄膜的相对电阻变化只有93%,而rGO 复合薄膜达504%,是前者的5倍以上,rGO复合薄膜的应变传感性能明显优于CNT 复合薄膜。这是由于一维结构具有较高的长细比,使得复合薄膜中的CNT 之间具有更多接触节点。拉伸后,CNT 的交错排列能有效地适应变形,同时保持了足够的接触节点。因此,与rGO复合薄膜相比,CNT 复合薄膜的相对电阻变化较小。
表1 所示为制备的rGO-CNF/PDMS 复合薄膜试样的基本参数,包括rGO-CNF 分散液用量、薄膜初始电阻、rGO 分布密度。rGO-CNF 分散液通过20 mg rGO和20 mg CNF分散于20 mL异丙醇中制得,PDMS 基底长×宽为20 mm×60 mm。图8 所示为薄膜初始电阻随rGO分布密度的变化。从图8可见:随着rGO 分布密度增大,薄膜初始电阻总体呈减小的趋势;当分布密度从0.50 g/m2增加到1.00 g/m2时,薄膜电阻变化较明显;当分布密度从1.17 g/m2变化到2.00 g/m2时,薄膜电阻几乎保持不变。

表1 rGO-CNF/PDMS复合薄膜试样的基本参数Table 1 Basic parameters of rGO-CNF/PDMS composite film samples

图8 薄膜初始电阻随rGO分布密度的变化Fig.8 Variation of initial resistance of films with rGO distribution density
当rGO 分布密度较小时,石墨烯片之间的距离较大,较难发生隧道效应,也无法形成导电通路,此时,复合薄膜接近于绝缘体,电阻很大。随着rGO 分布密度增大,石墨烯片之间的距离足够小而发生隧道效应,薄膜成为导体,电阻减小;随着分布密度进一步增大,石墨烯片之间相互搭接,形成了部分导电通路,电阻继续减小;当分布密度继续增大时,更多的石墨烯片搭接、重叠,形成稳定的导电网络,薄膜电阻也达到平稳状态,不再随分布密度的增大而发生较大变化。也就是说,随着rGO分布密度增大,薄膜的导电机理也发生变化;当rGO 分布密度从0.50 g/m2到1.00 g/m2,薄膜电阻急剧变化,在此区间内,薄膜的导电机理从隧道效应向导电通道理论过渡。
图9所示为2个代表性薄膜试样的相对电阻与应变的关系曲线。从图9可以看出:当应变在20%之内时,相对电阻与应变呈现较好的线性关系;随着应变进一步增大,相对电阻与应变呈现出近似指数增大趋势。通常采用灵敏度(K)来评价传感器的应变传感性能,它将传感器的相对电阻ΔR/R0与外部应变ε联系起来:

图9中曲线斜率即为该薄膜应变传感器的灵敏度。经计算复合薄膜1 的灵敏度K=24(应变为20%),明显比传统的金属应变片的灵敏度(约为2)大。对复合薄膜1在0~20%应变范围内进行重复拉伸试验,重复拉伸后的应变传感性能见图10。从图10 可见:当重复拉伸100 次时,灵敏度基本保持不变。复合薄膜传感器在重复拉伸作用下力电性能的微小变化可以用石墨烯片层滑动的低摩擦耗能来解释[13]。

图9 复合薄膜相对电阻变化与应变的关系Fig.9 Relationship between relative resistance change and strain of composite films

图10 复合薄膜1重复拉伸后的应变传感性能Fig.10 Strain sensing property of composite film 1 under cyclic tension

图11 不同初始电阻的复合薄膜相对电阻与应变的关系Fig.11 Relationship between relative resistance change and strain of composite films with different initialresistances
不同初始电阻的复合薄膜传感器相对电阻与应变(20%)的关系如图11所示。从图11可见:总体来说,传感器灵敏度随薄膜初始电阻增大而增大,高初始电阻的传感器对应变变化的敏感性较大。相对于传统的应变传感器,复合薄膜传感器的优势在于可以通过调整初始电阻将传感器灵敏度调整到一个特定值来代替传统传感器,或者根据具体需求进行调整,如测量低应变时调整到高灵敏度,测量高应变时调整到低灵敏度。
2.3 rGO-CNF/PDMS复合薄膜压阻机理
近年来,基于石墨烯的传感器研究逐渐增多,但其机理尚不明确,石墨烯的制备工艺和薄膜的质量差异是造成该机理不确定的主要原因。聚合物基弹性导体的压阻效应主要来自2个方面:1)导电填料的固有压阻性;2)由于电子传导接触条件变化而引起的压阻性,如接触点的断裂、接触面积和拉伸时的间距变化等。大尺寸单层石墨烯的压阻性已被证实,然而,石墨烯的六角晶格结构很难被破坏,拉伸程度非常有限,小尺寸石墨烯片之间由范德华力结合,在应力作用下较易发生相对滑动。本文的传感器是由小尺寸石墨烯碎片制备的,其压阻性主要是电子传导的接触条件发生变化而引起的。
rGO-CNF/PDMS 复合薄膜的导电机制是“隧道效应”和“导电通路”共同作用的结果。由于聚合物基底的电阻率远远大于导电填料的电阻率,可以忽略聚合物分子间电流,对于隧道效应占主导地位的复合薄膜(rGO 分布密度为0.50~1.00 g/m2)的电阻主要由电极间导电体和导电通道数目决定。需注意的是,这里的导电通道是指由隧道效应而形成的导电通道。石墨烯片自身的电阻很小,因此,复合薄膜的初始电阻R0可表示如下[20-23]:

式中:Rm为2个石墨烯片间由于隧道效应而产生的电阻;Rg为石墨烯片的电阻;N0为复合薄膜平行于电流方向的初始导电通道数;s0为石墨烯片之间的初始间距;l为平行于电流方向每个导电通道中的平均石墨烯片的数目;V为外加电压;J为隧道电流;m为电子质量;e为电子电量;h为普朗克常量;φ为相邻石墨烯片的势垒;a2为隧道效应的绝缘阻隔层有效面积。根据式(2)和(3)可得复合薄膜的初始电阻为

当复合薄膜在受到外界应力而发生形变时,石墨烯片之间的距离s、导电通路数N等均会发生不同程度的变化,从而导致电阻R发生改变,也就是出现所谓的压阻效应。相对电阻可表示为

其中,s0与导电填料的粒径、含量以及基体的弹性模量有关。当复合薄膜发生应变ε时,石墨烯片之间的距离s发生相应变化:

ε为聚合物基体的弹性应变,反映了基体随着长度变化导电网络发生破坏的程度。在应力形变作用下,导电通路数目可表示为[15]
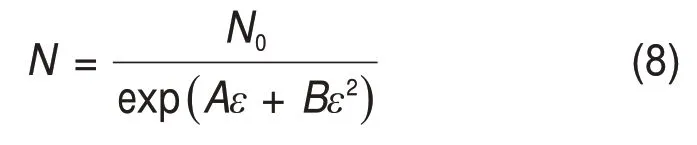
式中:A和B都是与导电填料有关的常量。将式(7)和(8)代入式(6)可得

则传感器灵敏度K可表示为

令C=γs0+A,当应变ε较小时,灵敏度K可表示为

式(10)和(11)表明:在小应变范围内,相对电阻与形变程度呈线性变化趋势,传感器灵敏度近似于曲线斜率C,与导电填料种类和浓度等因素有关;当拉伸程度不断加大时,在大应变范围内,电阻呈现指数变化的趋势,相应的传感器灵敏度也接近呈指数增大,这与由本文制得的传感器的实测结果是一致的。另外,式(11)也表明复合薄膜在应变作用下,灵敏度主要取决于导电填料的初始隧道间隙,可以通过增加石墨烯片层之间的初始距离来提高石墨烯应变传感器的灵敏度,即减小石墨烯的分布密度,前提是得保证片层间距足够发生隧道效应。
对于导电通道占主导机制的复合薄膜(rGO 分布密度大于1.00 g/m2),其电阻由导电体电阻Rg和接触电阻Rc决定,因此,复合薄膜的初始电阻R0可表示为

复合薄膜受力变形后的电阻R为

则复合薄膜电阻变化率为

石墨烯片之间的接触电阻可以表示为[24-25]

式中:R′c为薄膜变形后的接触电阻;a为与石墨烯片的表面状态、接触压力和电阻率相关的常数;S为石墨烯片的接触面积。当复合薄膜发生应变ε后,石墨烯片的接触面积可表示为

式中:b为初始状态下与石墨烯片接触方式相关的常数;S0为石墨烯片的初始接触面积;S′为薄膜变形石墨烯片的接触面积将式(15)和(16)代入式(14)可得

当应变ε较小时,灵敏度K可表示为

从式(18)可以看出:当应变较小时,传感器的灵敏度近似于1 个常数,这与实测结果相符。式(10)和式(17)显示了复合薄膜在应变作用下,灵敏度与导电体填料势垒、间距、接触面积和应变程度等有关。导电体填料的间距与其分布密度有直接关联,当减小填充材料的分布密度时,导电体的间距s0增大,灵敏度K会相应增大。然而,当分布密度较低时,复合薄膜电阻较大,不利于实际应用时传感信号的测量和获取,而较大的分布密度会导致复合薄膜力学性能发生显著变化,聚合物自身具有的优异回弹性和低模量等特性将无法得到继承和发挥,并且复合薄膜电阻率变化幅度以及灵敏度将变小。同时,在实验过程中,随着应变程度加大,电阻变化还与填充材料的掺杂效应、分散剂与材料间相互作用及导电材料在基体中的分散等有关,因此,需要在特定形变范围内研究填充材料种类和分布密度对复合薄膜应变特性的影响。
3 结论
1)CNF 能有效协助rGO 的分散,彼此之间交错搭接,也易形成便于离子和电子传输的多孔结构。
2)利用CNF 在异丙醇中搭载rGO 形成均匀稳定的rGO-CNF 复合物悬浮液,采用溶剂挥发法在PDMS 弹性基底上形成多孔隙结构的rGO-CNF 薄膜,再将液态PDMS 嵌入孔隙中,固化后制备了具有层状结构的柔性应变传感器。与直接在基底上堆积形成的单层石墨烯片层相比,避免了石墨烯纳米片与基底之间吸附力不足而导致的变形不协调问题,同时,弹性基底PDMS 良好的机械性能也使得传感器具有较强的拉伸能力和重复性,也能有效保护传感器不被轻易破坏,延长了传感器的使用寿命。
3)借助CNF形成的均匀稳定的rGO导电网络,使得传感器具有较高的灵敏度,并可通过控制工艺参数来调整,还可以通过控制柔性基底的厚度或材料种类来调整传感器的测量量程,传感器的柔性基底还可以适应不同表面形状的结构测量。
4)通过分析制备的一系列石墨烯复合薄膜传感器应变-电阻响应机理,建立了复合薄膜压阻行为预测理论模型,预测的应变与电阻的关系与实测结果相符。该柔性传感器具有较高的灵敏度和可靠性、优异的力学和压阻性能,其制备成本低且易于加工,有望应用于损伤探测和结构健康监测领域。
