基于信号相关的被动雷达导引头抗噪声源干扰方法分析
2020-05-18路瑜亮杨万君
路瑜亮,周 云,杨万君
(陆军装备部驻石家庄地区第一军代室,河北 石家庄 050081)
0 引言
如何对主波束内入射方向不同的2个目标进行分辨,一直是单脉冲雷达领域中的研究热点。在和差比幅测角体制下,对回波信号幅度固定的2个目标而言,当2个目标信号到达接收天线的相对相位符合0~2π均匀分布时,由单脉冲比所测得的角度均值会指向其中回波较强的目标;对于2个幅度符合瑞利分布的噪声源,由单脉冲比所测得的角的均值会指向二者的功率重心;对于1个幅度固定目标和1个幅度符合瑞利分布的噪声源,由单脉冲比所测得的角度的均值会指向与二者功率有关的二者位置中间的某一点,但该点并不是二者的功率重心[1-2]。对于回波信号幅度固定的2个目标,文献[3]提出了一种双脉冲的方法进行处理,从而获得2个目标的角度信息;文献[4]提出了一种基于相参积累的多目标分辨方法,而文献[5]则是针对均匀线阵自适应波束形成的情况提出了一种两目标分辨方法;而对于2个幅度符合瑞利分布的目标,文献[6-8]提出了不同的角度估计方法。针对四通道单脉冲体制,文献[9-10]提出了一种基于单采样点的两目标角度测量方法,但是该方法并不适用于普通单脉冲体制。
被动雷达导引头作为一种非相参的单脉冲雷达同样会遇到双点源或多点源干扰问题,文献[11-12]分别对于双点源宽带噪声调频干扰和窄带高斯噪声干扰的情况进行了分析,并利用不同的方法对2个点源进行分辨。本文将基于和差比幅单脉冲测角体制对被动雷达导引头主波束内存在1个幅度固定的辐射源(目标雷达)和1个噪声干扰源的情况进行分析,利用目标雷达信号自相关性强,噪声本身自相关性差以及噪声和雷达信号之间互相关性差的特点对和、差通道信号进行相关处理,从而有效降低噪声源对目标测角的影响。
1 信号模型及分析
假设目标雷达和噪声源的角度分别为θ1,θ2,雷达和噪声源信号在到达导引头接收天线前的复包络分别为A(t),B(t),导引头天线的和、差方向图分别为gS(θ),gD(θ),此时,导引头接收机的和、差通道信号的复包络分别为:
S(t)=gS(θ1)A(t)+gS(θ2)B(t),
(1)
D(t)=gD(θ1)A(t)+gD(θ2)B(t) 。
(2)
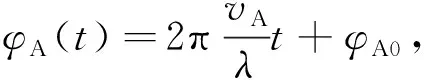
在只有目标雷达存在的情况下,一般通过对和差通道的单脉冲比取实部就可以得到目标的角误差信息:
(3)
式中,k为测角的误差斜率。

2 基于信号相关分析的原理
通过分析可以看出,在噪声源干扰存在的情况下,通过传统的单脉冲方法很有可能无法得到目标雷达的角度信息。即使在噪声调频干扰的情况下,噪声源的功率往往大于目标雷达的副瓣功率,此时通过对单脉冲比实部求均值得到的也是干扰源的角度。

E[B(t)B*(t-τ)]≈0,
(4)
同时,由于雷达信号和噪声源之间的不相关性,有:
E[A(t)B*(t-τ)]≈E[B(t)A*(t-τ)]≈0 。
(5)
分别对和、差通道信号复包络取其自相关:
RS(τ)=E[S(t)S*(t-τ)],
(6)
RD(τ)=E[D(t)D*(t-τ)] 。
(7)
将式(1)、式(4)和式(5)带入式(6)可得:
RS(τ)=E{[gS(θ1)A(t)+gS(θ2)B(t)]·
[gS(θ1)A*(t-τ)+
gS(θ2)B*(t-τ)]}≈
E[gS2(θ1)A(t)A*(t-τ)]=
(8)
所以:
|RS(τ)|=gS2(θ1)|A|2。
(9)
同理可得:
(10)
|RD(τ)|=gD2(θ1)|A|2。
(11)
根据式(3)、式(9)和式(11),有:
(12)
由式(12)可以得到目标雷达的角误差信息η1的绝对值,但会失去η1的符号信息,是由于在计算自相关时将gD(θ1)进行了平方运算。为了避免这一点,取和、差通道信号的互相关:
(13)
所以,带有符号的角误差信息可以通过式(14)获得:
(14)

(15)
3 仿真分析
采用部分2中的信号模型分别对噪声调频干扰以及高斯噪声干扰存在的情况进行仿真,噪声调频干扰以及高斯噪声干扰的带宽均为5 MHz,采样时间为Δt=2.5 μs,可以认为对噪声的相邻2个采样点之间是不相关的,以Δt为时间间隔进行相关运算,然后按照式(15)求取目标角度。假设噪声源的角度信息为η2=0.2,分别在目标雷达角度信息为η1为-0.1,-0.01以及信噪比为-10,0 dB的情况下,用Monte Carlo方法进行1 000次仿真,进行统计得到测角均值和均方根误差随采样点数变化的情况,如图1和图2所示。采样点数为1 200,目标雷达角度信息η1分别为-0.1,-0.01的情况下,得到的测角均方根误差随信噪比的变化如图3所示。
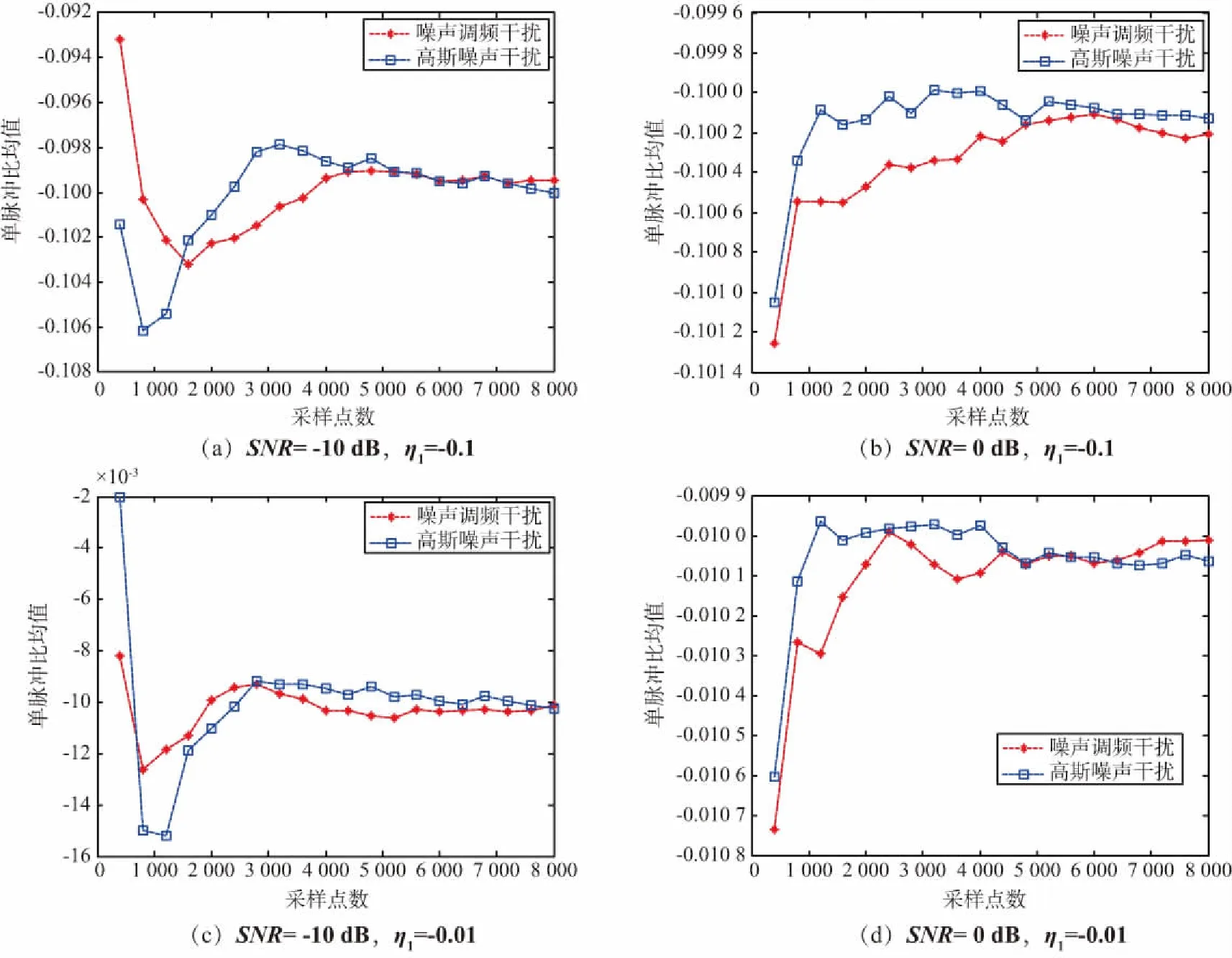
图1 测角均值随采样点数的变化Fig.1 Variation of the mean value of angle measurement with the number of sampling points

图2 测角均方根误差随采样点数的变化Fig.2 Variation of RMSE of angle measurement with the number of sampling points
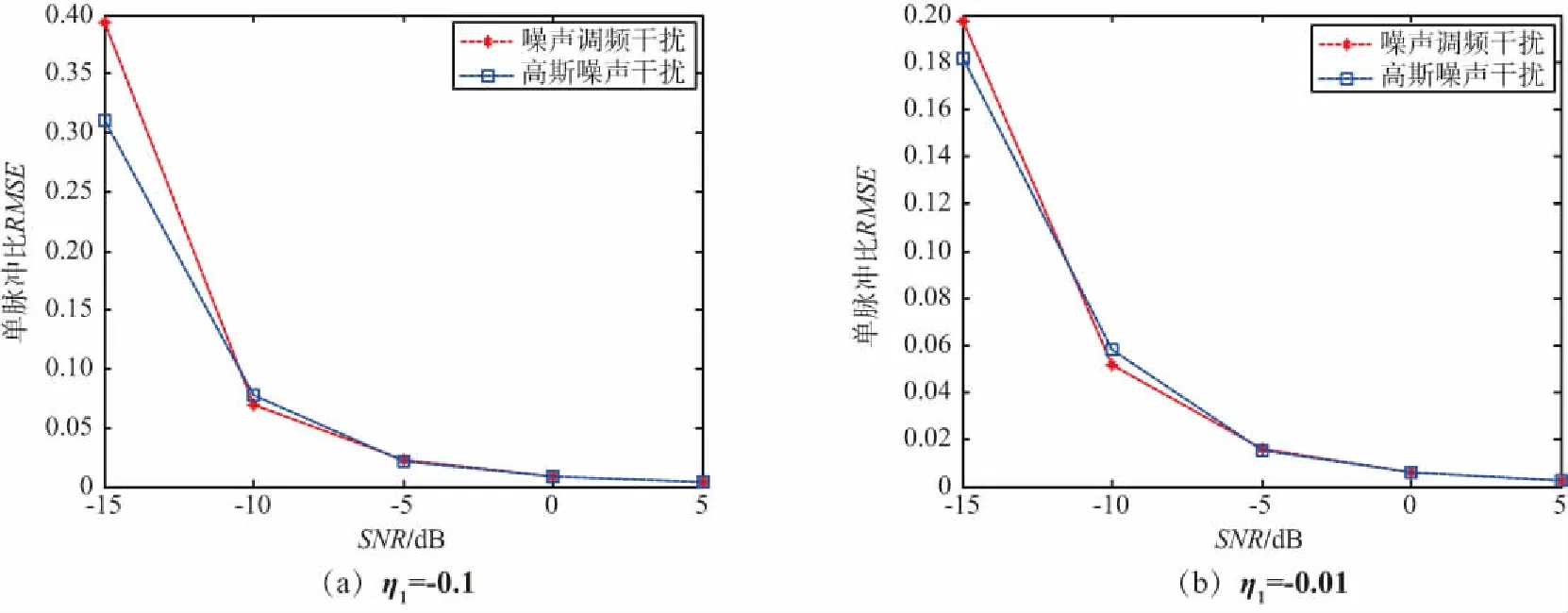
图3 测角均方根误差随信噪比的变化Fig.3 Variation of RMSE of angle measurement with SNR
由图1~图3可以看出,本文提出的方法对噪声调频干扰和高斯噪声干扰的抑制性能基本一致,只要采样点数足够多,得到的测角均值很接近于真实目标角度,并且随采样点数的增加,测角的均方根误差会逐渐变小。采样点数相同的情况下,测角的均方根误差会随着信噪比的增大而减小。
4 结束语
在目标雷达信号和噪声干扰信号同时存在的情况下,利用各信号分量的相关特性,提出了对和差通道信号求互相关以及对和通道信号求自相关,然后对二者比值取实部求目标雷达角度的方法。理论上证明了该方法的正确性,并通过仿真验证了该方法的有效性以及在不同信噪比情况下该方法的性能。
