对音叉接触纸张的“低音”现象研究

马茂杰 周廷明 张 君

(四川省成都市温江中学 四川 成都 611130)

赵芸赫

(首都师范大学附属中学 北京 100048)

当一个音叉在一张纸上振动时(图1)(其间的接触很弱)，所发出的声音频率可以低于音叉发声的基本频率.在进行实验的过程中，我们的确能够采集到低于音叉基频的稳定声音频率，与此同时的是在整个系统的声音中还存在着更高的声音频率 .其频率接近于音叉基频的整数倍.通过查阅文献，我们了解到高次频率的出现可能正是泛音现象，即驻波原理.但是在相应的文献中却并未提及低音现象的成因.因此，我们将在本研究中探究低音现象的成因，提出理论模型，并在实验上给予其定性的验证.

图1 音叉和纸张

1 理论模型

1.1 系统振动模型

在探究的问题中，由于并未对纸张的固定方式进行限制，因此存在多种可能.在预实验中，我们尝试了对纸张的3种固定方式，即单边固定、对边固定以及悬挂固定.在此3种方式中，单边固定时能出现较为稳定低音现象，对边固定则难以出现低音现象，而悬挂固定则由于纸张的弹飞，无法得到较为稳定的低音频率.因此将在本研究后续过程中，皆采用对纸张采用单边固定的方式.

当纸采用图2所示的单边固定方式,即纸张满足一边固定、三边自由的振动方式，则在音叉与固定纸张所组成的系统中，可将纸张及其固定支架视作“悬臂梁”，而音叉则对“悬臂梁”提供外界的周期性简谐激励.于是可以将整个系统的振动模式建立模型为“悬臂梁的受迫振动”.

图2 采用单边固定方式的纸张

1.2 纸张的自由振动模型

考虑纸张在振动时，正面截面在弯曲变形的过程中始终保持为平面，即忽略截面绕中心轴转动(过形心使截面上下对称的轴)的惯性效应和截面的剪切形变.则可使用梁的简化模型——欧拉-伯努利梁模型来进行纸张的振动分析.

对于一张密度为ρ，长为l，厚度为b，高为h，弹性模量为EI的纸张(其中长宽高的定义如图3所示)，通过查阅文献[1]知应满足如下的振动方程

(1)

其中w(x,t)是位移(即挠度)，f(x,t)是沿弯曲方向的负载.

图3 纸张的长宽高

讨论纸张自由振动时所满足的方程，给出悬臂梁的边界条件后进行求解，根据文献[1]中的求解知，得到对应各阶的固有频率为

(2)

(3)

对于一般纸张的振动形式应满足图4所示的一阶振动，并且由于本实验主要在于对基频的探究，取i=1,则式(3)可进一步化为

(4)

图4 前三阶振动图示

1.3 音叉的简谐激励下系统的振动

接下来考虑音叉所带来的简谐激励影响.

通过查阅文献[2]知，系统在简谐力作用下的受迫振动，在初始阶段的系统响应是暂态响应与稳态响应的叠加.在暂态响应中，整个系统响应是由3部分所叠加而成，即初始条件引起的自由衰减振动、简谐激励引起的伴随自由振动以及简谐激励引起的纯粹强迫振动.引用文献[2]中的图示(即图5)可知，系统的响应会由一段时间的叠加频率过渡到激振频率，在此期间若激振频率高于系统的固有频率时，则可在暂态响应中出现中明显的低音现象.

图5 暂态响应中的频率叠加

因此，低音产生的主要是源于纸张初始的自由振动.其频率取决于纸张初始自由振动的频率.

根据所求得的公式，在其他条件不变时，下面几种情况都会使纸张固有频率降低，进而导致系统的低音频率降低，即：

(1)当纸张弹性模量减小时；

(2)纸张长度增加时；

(3)纸张侧面的高减小时；

(4)纸张侧面的宽减小时.

值得注意的是，由于在具体的实验中很难对初始条件即简谐力的施加时机进行控制，故每次实验得出的频谱图具有不唯一性.正是由于这个缘故，在此后的实验中只能从整体趋势上来对理论进行定性的验证.

2 实验探究

2.1 实验装置及设计

实验装置(图6)包括铁架台、音叉、海绵(固定且避免带动装置振动)、限制装置(控制纸与音叉的接触程度)、手机(采集音频)、固定支架、固定夹.

图6 实验装置

在实验过程中，先用敲击器敲打音叉，然后再转动支架使得音叉与纸张接触，等待声音频率趋于稳定时，对音频进行采集，最后再导入软件Adobe Audition对其进行频谱分析.

因材料所限，暂且无法对纸张的密度ρ，纸张的弹性模量E进行实验探究.因此接下来的探究包括4个部分：纸张厚度、纸张高度、纸张的长度以及纸张的褶皱程度.

2.2 探究纸张厚度对低音频率的影响

选取同种厚度不同的素描纸(长×宽=10.00 cm×5.00 cm)，其厚度分别为0.32 mm，0.22 mm，0.15 mm.

根据实验数据作出纸张厚度对低音频率的影响图像，如图7所示，由图可知，在其他条件一定的情况下，随着纸张厚度的增加，低音频率呈上升趋势.符合理论预测.

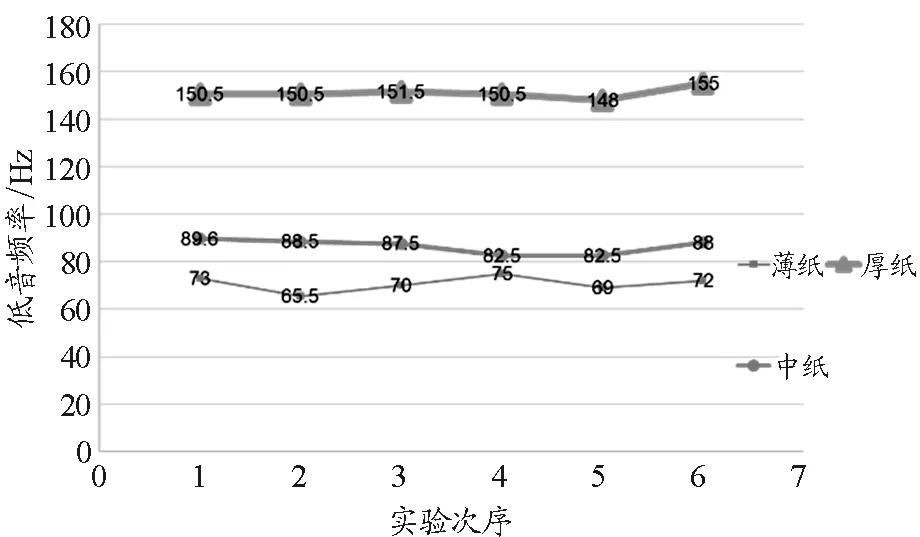
图7 纸张厚度对低音频率的影响

2.3 探究纸张高度对低音频率的影响

选取3张同种纸张，其长度皆为6.00 cm，高度依次为6.00 cm，4.00 cm，2.00 cm.作出纸张高度对低音频率的影响图像，如图8所示.

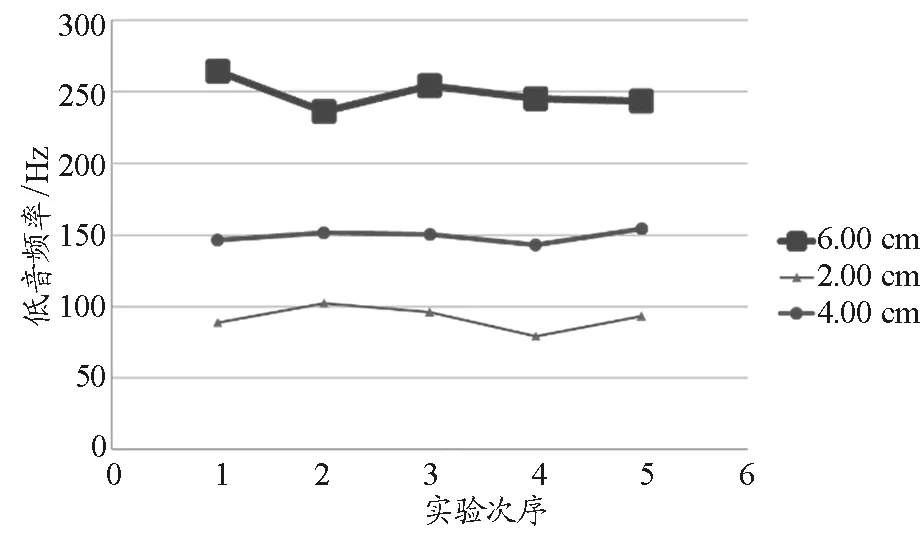
图8 纸张高度对低音频率的影响

由上图知，在其他条件一定时，随着纸张高度的增加，低音频率的值也随之增高.符合理论的预测.

2.4 探究纸张长度对低音频率的影响

对于纸张长度的讨论，我们认为其中存在有两种不同的情况.一种是对于击打位置不同所引起的纸张有效长度的改变.另一种则是由纸张本身长度不同所引起的.

在第一种情况中，对于同一张纸，将其划分为9个区域,如图9所示，分别记录每个区域产生的低音频率.(击打位置皆为每个区域的中轴，图中数值代表每个边界分别到右边界的距离)

图9 纸张分区图示

根据所得数据，作出单张纸的长度分区对低音频率的影响图像，如图10所示.

图10 探究单张纸的长度分区对低音频率的影响

由上图的统计数据知，对于同一张纸，距离固定边界越远的区域，产生声音的频率会更低.

在第二种情况中，选取等宽(6.00 cm)的3张同种水彩中纹纸，其长度依次为6.00 cm,11.00 cm,16.00 cm(固定纸张所消耗的长度为1.00 cm，即实际有效长度分别为5.00 cm,10.00 cm,15.00 cm，如图11所示).

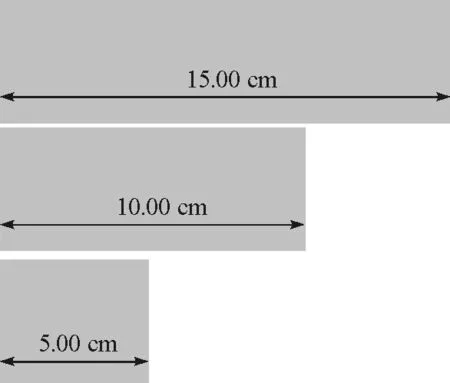
图11 3种纸张示意图

对于数据采集，我们依然分区讨论的方式来比较在该种情况下纸张长度对低音现象出现的影响.得到的数据如表1所示.

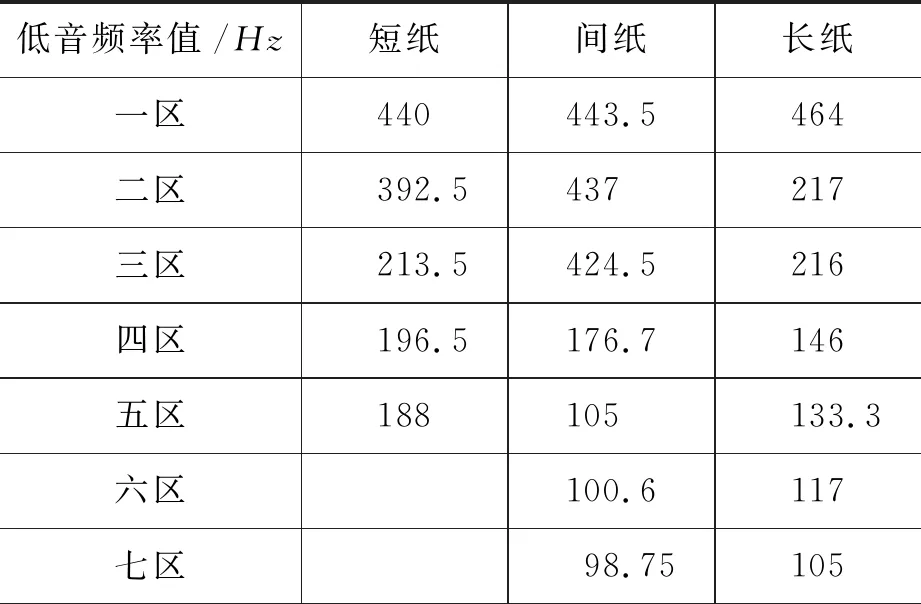
表1 多张纸的不同长度分区对低音频率的影响

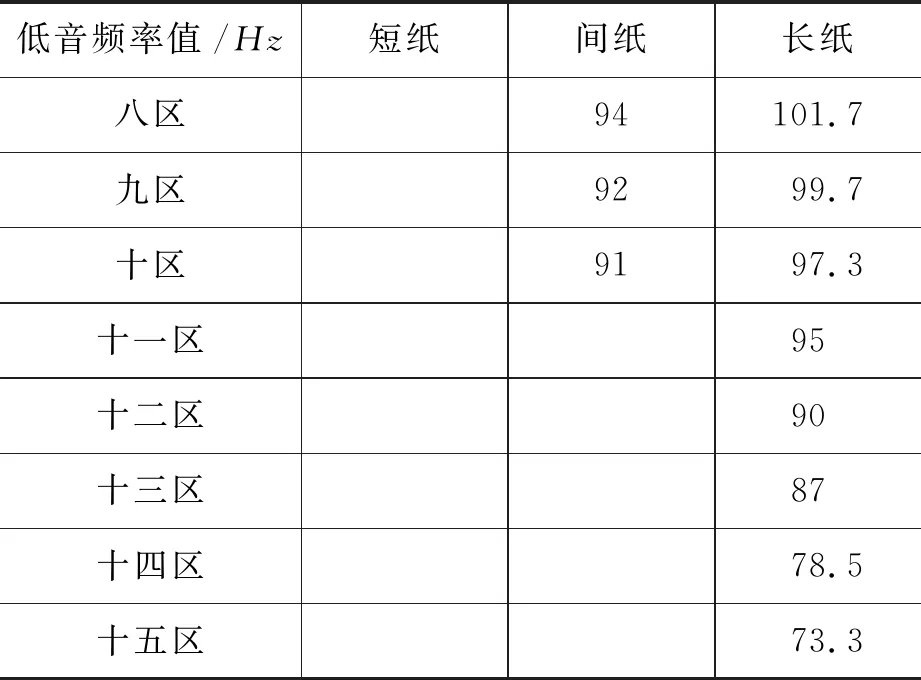
续表1

由上表的统计分析可得，在其他条件一定时，根据纸张的长度比例1∶2∶3，在相应的比例分区中，低音频率值呈现随纸张长度增加而降低的趋势.

若以短纸的一区、间纸二区和长纸三区为一组，短纸二区，间纸四区和长纸六区为二组，以此类推，可得到如图12每组中3种纸的频率对比.

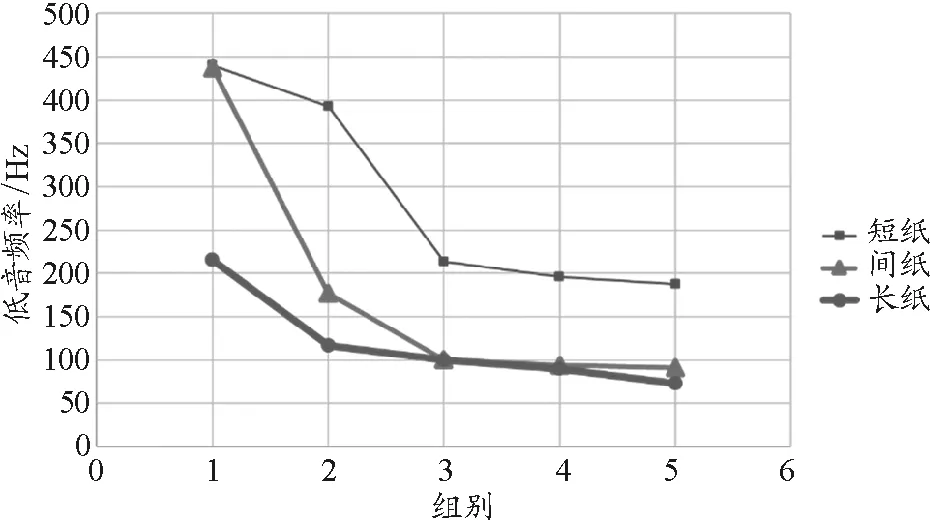
图12 每组频率对比

同时我们也注意到，在实验过程中这3种纸中都存在这样的现象：开始时，频率随分区增大而稳步下降，而后在两个相近的分区频率急剧下降的现象，此后频率的下降再次趋于稳定.

由以上两种对纸张长度的讨论，可知在两种情况下都有随着纸张长度的增加，所产生的低音频率会呈现下降趋势，符合理论的预测.

2.5 探究纸张褶皱程度对低音频率的影响

选取两组不同(素描纸与打印纸)的纸张(纸张大小：长×宽=8.00 cm×8.00 cm).每组纸张均为同种等大的纸张.在每组中存在经过褶皱处理的纸张和未经处理的原纸张.实验得到的图像如图13和图14所示.

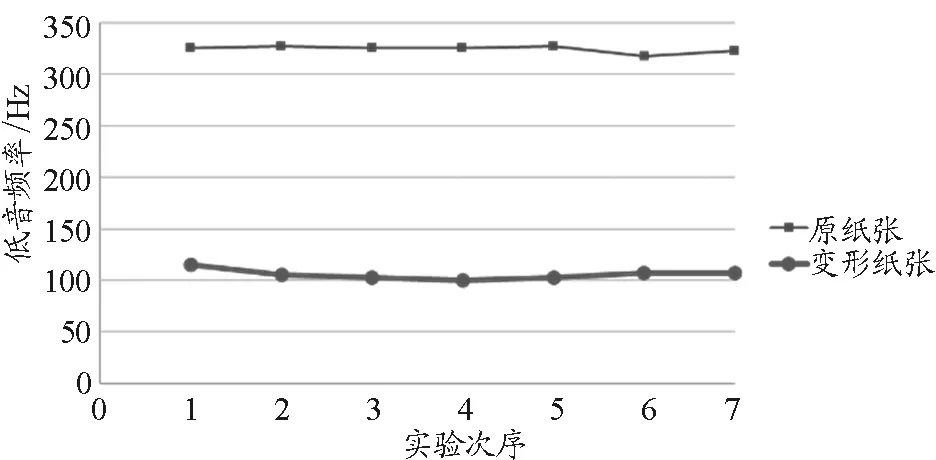
图13 褶皱对低音频率的影响(一组)

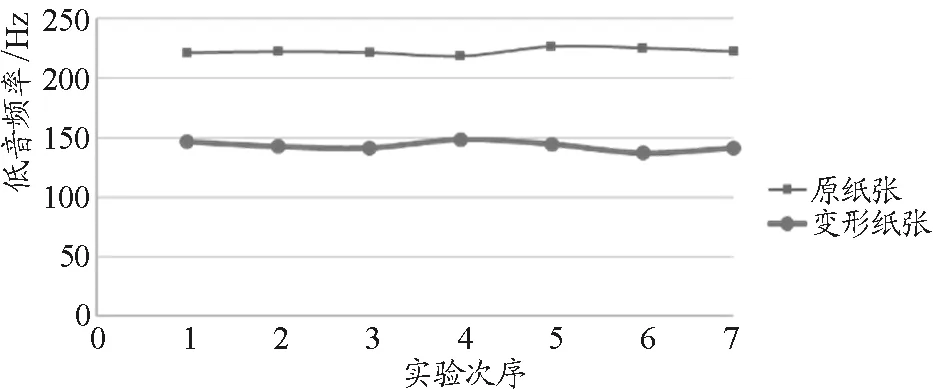
图14 褶皱对低音频率的影响(二组)

在两组数据中，原纸张的低音频率均高于变形纸张的低音频率.即有如下的结论：在其他条件不变时，纸张的褶皱程度越大，则在低音现象中，其频率更低.

另外，我们认为经过褶皱处理的纸张的低音频率降低的可能原因是其弹性模量发生了改变(减小)，继而导致其固有频率减小.

3 结论

本研究针对音叉接触纸张的低音现象进行了研究，通过观察实验现象，得到在同一音叉的相同激励下，低音现象与纸张的固有性质有关的结论,基于此建立了悬臂梁的受迫振动理论模型对该现象中低音现象的产生进行了解释，得到纸张的长度、宽度、厚度、弹性模量和密度对低音频率的影响关系，据此，设计了实验分别验证了纸张的长度、宽度、厚度和褶皱程度这4个变量对低音的影响，得到低音频率随纸张的长度增加、厚度减小、宽度减小、弹性模量减小而降低的结论.