刍议带电粒子在电磁场中的运动轨迹
2020-05-18李燕
李 燕
(雅安职业技术学院智信学院 四川 雅安 625000)
1 引言
若只有电场时,一质量是m,带电荷量为q的粒子以速度v0射入一场强为E的匀强电场中,当带电粒子的运动方向与电场方向垂直时,带电粒子受到电场力F=qE的作用而做抛物线运动,如图1所示.当带电粒子运动方向与电场方向平行时,带电粒子做匀加速直线运动.
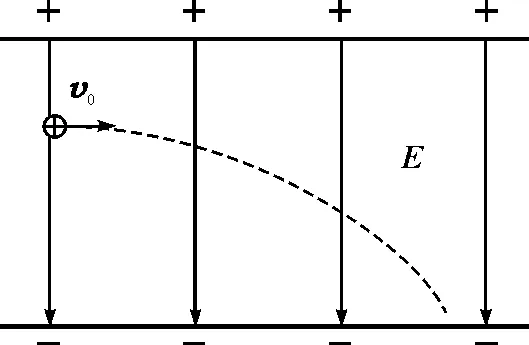
图1 v0垂直射入电场
若只有磁场时,如图2所示,带电粒子以速度v与磁场方向成θ角进入匀强磁场B中,可把v分解为v⊥和v//,带电粒子一般做螺距相等的圆柱螺旋运动,其运动轨迹是一条螺旋线,如图3所示.带电粒子在磁场中的螺旋运动广泛地应用于“磁聚焦”技术,例如电子显微镜的应用.当带电粒子的速度v与B平行时,带电粒子作匀速直线运动.当带电粒子的速度v与B垂直时,带电粒子做匀速圆周运动.
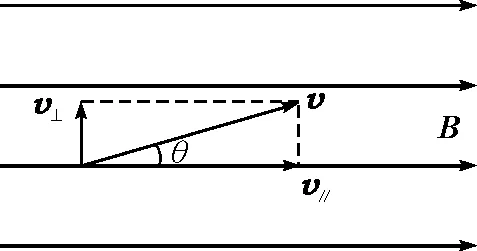
图2 v分解为v⊥和v//
若电场和磁场同时存在时,有的学生常常会认为带电粒子的运动轨迹是电场和磁场单独存在时带电粒子运动的简单迭加.一般我们知道在只有磁场时,带电粒子受到洛伦兹力作用,但洛伦兹力只改变带电粒子的运动方向,不会改变其速率,因为洛伦兹力F=qv×B,所以洛伦兹力的大小也不会改变.但如果电场和磁场同时存在时,带电粒子的速率将改变,所以洛伦兹力的大小就会改变.这样,带电粒子受到的合力为F=q(E+v×B),下面我们分别讨论两种特殊情况下带电粒子的运动轨迹.
2 当电场E与磁场B平行时
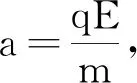
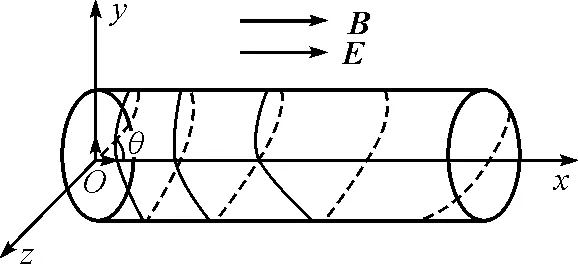
图4 螺距改变的圆柱螺旋运动
如图4中所示,洛伦兹力只与垂直于x轴方向的速度vsinθ有关,所以带电粒子在yOz平面内,在洛伦兹力的作用下以速度vsinθ做匀速圆周运动,其圆周运动的半径
圆周运动的周期
由于带电粒子在x轴方向的匀加速直线运动和在yOz平面内的匀速圆周运动互不影响,所以带电粒子的合运动是二运动的迭加,带电粒子做螺距改变的圆柱螺旋运动.因为螺距是每经过一周期带电粒子在x轴方向前进的位移,位移随时间变化,所以螺距随时间不断变化,带电粒子运动轨迹如图4所示.
3 当电场E与磁场B垂直时
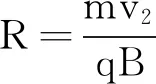
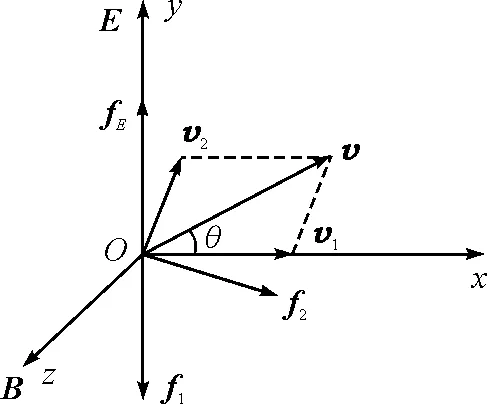
图5 电场与磁场垂直时
由以上分析可知,当电场E与磁场B垂直时,带电粒子的运动是匀速直线运动和匀速圆周运动两部分运动的迭加,所以带电粒子的运动轨迹是两种运动迭加的结果,其轨迹如图6所示为摆线,又称为旋轮线.图6所示带电粒子一方面以速度v1做匀速直线运动,同时又以速度v2做匀速圆周运动.
(1)当v1=v2时,带电粒子运动轨迹是普通的旋轮线,如图6(a)所示;
(2)当v1 (3)当v1>v2时,带电粒子运动轨迹是短辐旋轮线,如图6(c)所示. 图6 当E与B垂直时,带电粒子的运动轨迹 因为带电粒子的运动轨迹是比较复杂的问题,在这里我们仅仅讨论了带电粒子的速度v在垂直于磁场方向的xOy平面上的情况. 通过以上讨论,我们应明白当电场E与磁场B同时存在时,带电粒子的运动并非电场和磁场单独存在时带电粒子运动的简单迭加,因为在没有电场时,洛伦兹力只改变带电粒子运动的方向,不改变其速度的大小,所以洛伦兹力的大小也不改变,但是有电场存在时,带电粒子速率改变,洛伦兹力大小也要改变,所以不能进行简单的迭加,而应分不同情况进行讨论.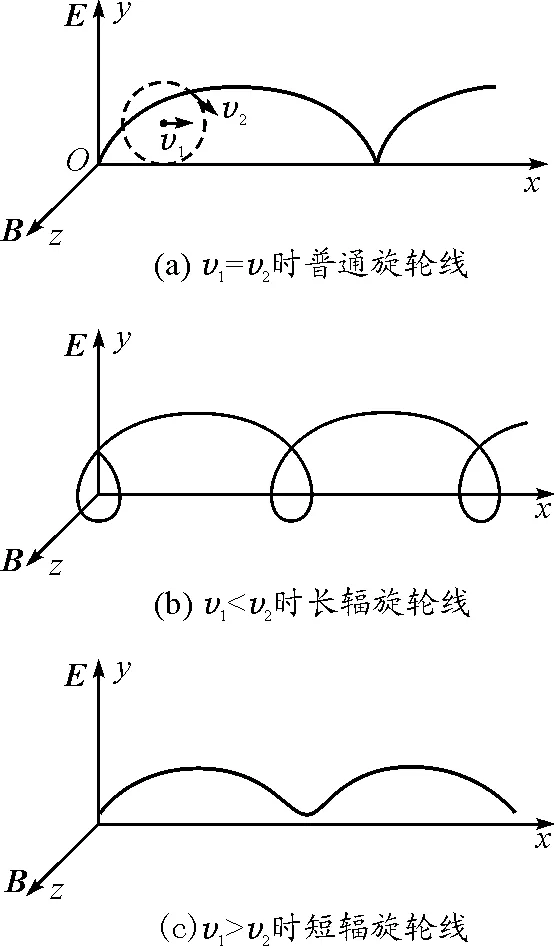
4 结束语
