基于Mathematica的均匀带电细圆环电场模拟*

高 峰 吕 刚 韩 岳 曹学成 姜贵君 赵文丽

(山东农业大学信息科学与工程学院 山东 泰安 271018)

1 引言

均匀带电细圆环是大学物理电磁学中一个典型的物理模型．在一般的教材[1]中只计算圆环轴线上的电场强度和电势分布，鲜少讨论该带电体系在全空间中的电场和电势．因此，学生很难对该体系在全空间的电场和电势分布有整体的认识．对于这个问题，有人已经进行了一些研究．文献[2]和[3]分别在直角坐标系和柱坐标系中导出电势和电场强度的级数解；文献[4]使用直接积分的方法分别把电场强度表示为椭圆积分和勒让德多项式．但这些计算结果仅仅以数学表达式的形式给出，学生很难从公式中把握电场的特点．文献[5]用数值积分的方法计算椭圆积分, 求出圆环平面上的场强与电势，讨论的范围仍然不够完整．文献[6]利用 Matlab数值计算功能对均匀带电细圆环在空间激发的电场进行了讨论，做出了过环心与圆环垂直的平面内的等势线和三维空间的等势面，形象地给出圆环周围电场的空间分布．但该文献讨论问题略显单薄，与课堂教学结合仍需拓展．

Mathematica软件是由沃尔夫勒姆研究公司(Wolfram Research Inc.)研发的一款数值计算和可视化软件，可以解决各种领域复杂的符号计算和数值计算的问题，也可以方便地画出各类图形，从而形象地表示出函数的某些特性，是目前为止使用最广泛的数学软件之一．本文利用这一款计算软件对均匀带电细圆环在空间激发的电场进行了计算，实现了电场和电势的可视化，形象展示了该体系静电场的空间分布，为学生全面掌握这一模型提供了极大的帮助．

2 理论模型与处理

如图1所示，半径为a的均匀带电细圆环，带电荷量为q，以圆心为坐标原点建立直角坐标系，x轴与y轴在圆环面上，z轴与环面垂直．假设在空间中取一场点P(x,y,z)，则应用点电荷的电势计算公式，在带电细圆环上取线元dl，dl所在半径与x轴的夹角为θ，带电荷量为

则该电荷元在P点的电势

dU(x,y,z)=

则整个带电细圆环在P点的电势

其中

ε0=8.85×10-12C·N-1·m-2

为真空电容率，为了便于计算，我们取

q=2π×4πε0a=1 m

则上式化简为

根据电场强度和电势之间的关系E=-U，可以得到空间的电场强度分布．

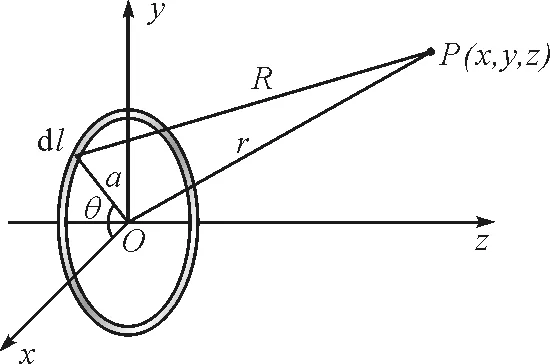
图1 均匀带电细圆环

上述理论处理过程并不难理解，但是关键的问题是电势的积分无法用初等函数表示，对电势求梯度更是一项复杂的工作．如果将上述复杂的积分计算工作交给Mathematica处理，问题就变得简单多了．

3 电场强度和电势的计算及可视化

3.1 与xOy平面平行的平面内的电场分布

在圆环平面(即xOy平面)，有z=0，坐标选择的范围为-3a≤x≤3a，-3a≤y≤3a．使用Mathematica的ContourPlot 命令绘制等势线图，如图(2a)所示．其中，等势线数值参数Contours取30，颜色参数ColorFunction取Hue[#]&，显示等势线数值即ContourLabels -> All．从图中可以看出电势的分布是内密外疏的轴对称分布，范围是1.85 V≤U≤9.62 V．在带电细圆环的外部区域和内部区域，越靠近圆环电势越大．值得注意的是，图中数据表明当电势较高时(6.29 V≤U≤9.62 V)，等势线在带电圆环内外两侧各有一条，而电势较小时(U≤6.29 V)，等势线只有一条，分布在圆环外侧．使用Plot3D和StreamPlot的命令，分别作出电场强度大小和电场线分布图，图2(b)画出了E≤100 V/m的电场强度，显然，在圆环周围区域，越靠近带电细圆环，电场强度越大．为了更好地显示电场线与带电细圆环的对应关系，图2(c)中使用ParametricPlot命令在电场线图中加入了带电细圆环．设圆环带正电，则电场线的方向在带电细圆环内外是反向的．图2(d)将电势分布和电场线分布组合在一起，形成常见的电场分布图．

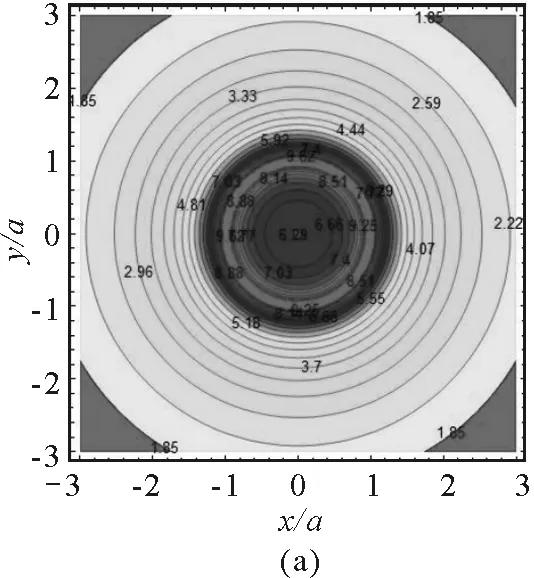
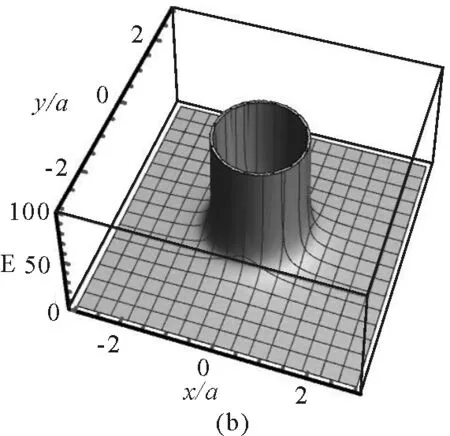
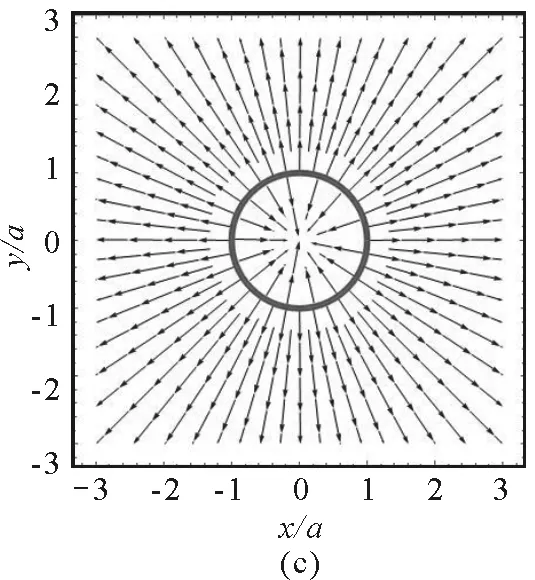
图2 xOy平面内的电场分布

以上的讨论是圆环平面内的电场和电势分布，那么在与圆环平面平行且z≠0的平面内的电场分布情况如何？对以上程序略做修改即可看到结果.图3是与xOy平面平行且z=2a平面内的电场强度和电势与电场线的分布．从图3(a)可以看出，在该平面内x=0,y=0处的电场强度接近于零，随着与中心对称轴线距离的增加，电场先增加后减小，到中轴线的距离接近于a时达到最大值，电场强度E≤0.6 V/m．图3(b)中电势的取值范围为1.41 V≤U≤2.773 V，相对于xOy平面电势的外疏内密分布，该平面内的电势分布较为均匀．

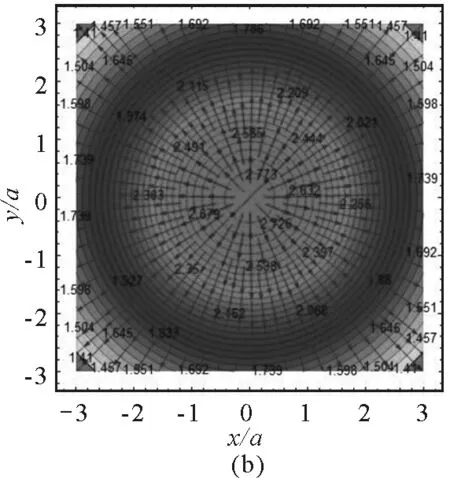
图3 与xOy平面平行z=2a平面内的电场分布

3.2 与xOy平面垂直的平面内的电场分布

上面讨论的是与圆环面平行的平面内的电场分布．那么与圆环面垂直的不同平面内的电场分布呢？我们以xOz平面和与该平面平行的y=a的平面为例进行讨论．在xOz平面内的电势电场分布如图4所示．

图4(a)给出的是电势的分布，从图中可以看出，等势线具有明显的轴对称性，并且越向外越接近于圆，也就是说，在远离带电圆环的区域，电势的分布类似于将电荷量集中于圆心的点电荷的电势分布．越靠近带电细圆环，等势线变密，为类椭圆．在细圆环内部区域，等势线又从类椭圆分裂成两个凸轮的形状．电势的范围为1.7 V≤U≤7.2 V．图4(b)和图4(c)分别为电场强度大小和电场线分布．从图4(b)可以看出，越靠近带电细圆环，电场强度越大，并且有对称分布，图中画出了E≤30 V/m的电场强度．从图4(c)可以看出，电场线的分布明显具有左右对称性．图4(d)将电势分布和电场线分布组合在一起，形成常见的电场分布图．

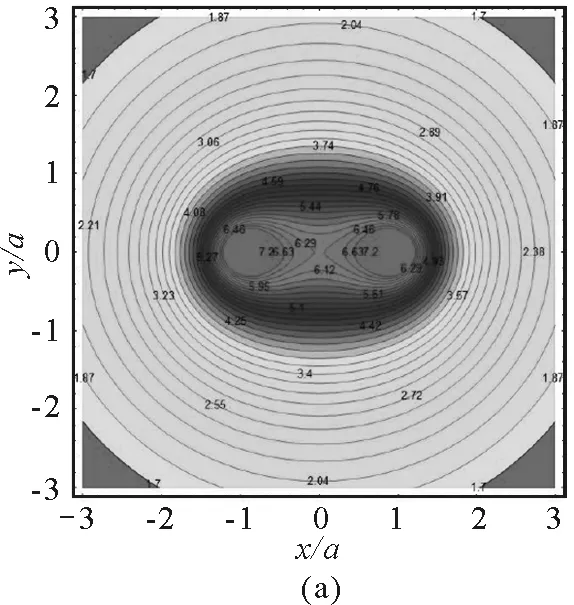
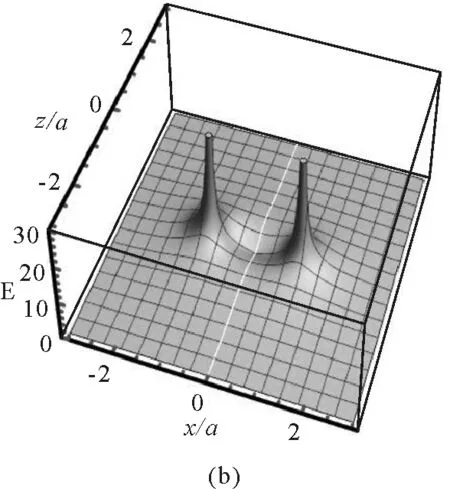
图4 xOz平面内的电场分布

在与xOz平面平行且y=a的平面，该平面与带电细圆环相切，位置比较特殊．其电场电势分布如图5所示．从图5(a)可以看出，电场强度已经从左右两个极值转换为单极值．从图5(b)的电势和电场线分布可以看出，电势的分布仍然满足外圆内类椭圆的情况，不同的是，在进入带电圆环的内部区域后，类椭圆不再分离为凸轮形状，仍然是一个整体，电势的范围为1.54 V≤U≤5.6 V．

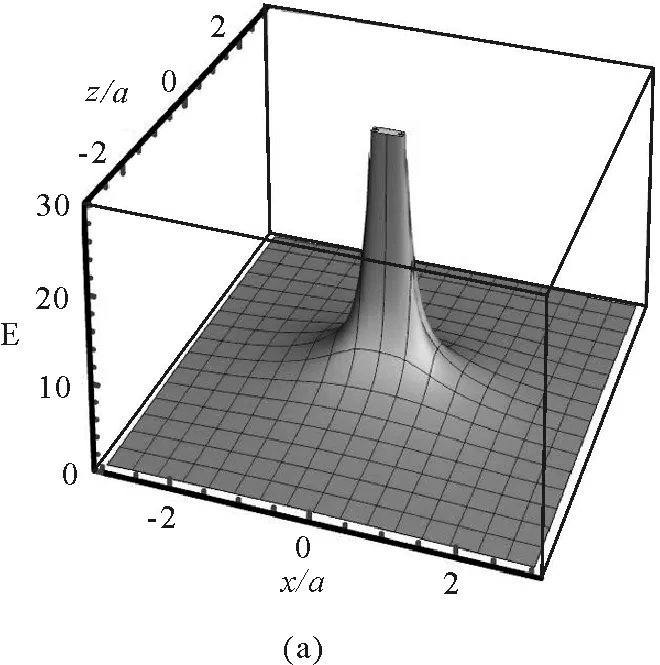
图5 与xOz平面平行y=a平面内的电场分布

3.3 三维空间的电场分布

需要说明的是，在图中中心画出的带电圆环并不是计算结果，而是为了清晰地显示带电圆环的电场分布，使用ParametricPlot3D命令加在电场线中额外附加的．

图6 三维空间的电场分布

4 结论

本文应用Mathematica软件对均匀带电细圆环全空间的电场和电势分布进行了讨论，绘制了不同观察角度下的电场和电势图，深入分析了圆环周围不同位置电场的特点，最后还画出了三维空间的电场和电势分布．通过电场可视化，使得抽象的问题变得形象，枯燥的电场变得生动起来，非常有助于提高教学效果．