带电粒子在矩形边界匀强磁场中经过某一点的问题
2020-05-18周胜
周 胜
(安徽省宿城第一中学 安徽 宿州 234000)
带电粒子在有界匀强磁场中的运动一直都是高考中的高频考点,2019年也不例外,3套全国卷分别以不同的方式考查了这一内容.全国Ⅰ卷以计算题的形式考查了带电粒子在三角形边界匀强磁场中的偏转问题,全国Ⅱ卷以选择题的形式考查了带电粒子在正方形边界匀强磁场中的偏转问题,全国Ⅲ卷也以选择题的形式考查了带电粒子在两个直线边界匀强磁场中的偏转问题,总体难度不大.事实上,在平时的教学中,关于带电粒子在匀强磁场中的偏转问题,题目变化多种多样,采用的方法也不尽相同,因此也是教师教学以及学生学习的难点.为了突破这一难点,教学同行们从各个角度对这一问题进行了分析与研究.有教师总结了带电粒子在磁场中运动的基本模型[1],不同有界磁场中的圆周运动的处理方法[2],确定圆周运动确定带电粒子在直线边界磁场中运动轨迹的方法[3],利用“旋转圆”与“缩放圆”方法解决带电粒子做圆周运动的临界问题[4],以及利用巧妙方法处理带电粒子在磁场中的偏转问题[5,6]等等.2019年全国Ⅱ卷的第17题以及平时在教学中遇到的问题,引起了笔者对带电粒子在矩形边界匀强磁场中经过某一点的问题的思考.
1 遇到的问题
如图1所示,正方形abcd区域内有垂直于纸面向里的匀强磁场,O点是cd边的中点.若一个带正电的粒子(不考虑重力)从O点沿纸面以垂直于cd边的速度射入正方形内,经过时间t0刚好从c点射出磁场.现设法使该粒子从O点沿着纸面以与Od成30°的方向(如图1中虚线所示),以各种不同的速率射入正方形内,那么下列说法正确的是( )
A.该带电粒子不可能刚好从正方形的某个顶点射出磁场
B.若该带电粒子从ab边射出磁场,它在磁场中经历的时间可能是t0
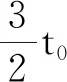
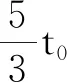
分析:对于B,C,D 3个选项而言,通过几何分析与计算可以较为轻松地判断出选项B和C错误,选项D正确.而本题比较复杂的就是对选项A正误的判断,即粒子能否从a点射出磁场,通常可以采用“伸缩圆”[4]的方式通过圆规逐个画圆来判断随着粒子速度的增大,粒子先与ad边相切还是能够直接经过a点,也可以进行理论分析与证明.但是花费的时间较长且可能分析出错,能不能通过图形的几何关系更快地得到相应的结果呢?
2 解决思路
为了更加快捷地解决这一问题,笔者在教学中鼓励学生采用以下思路,如图2所示.
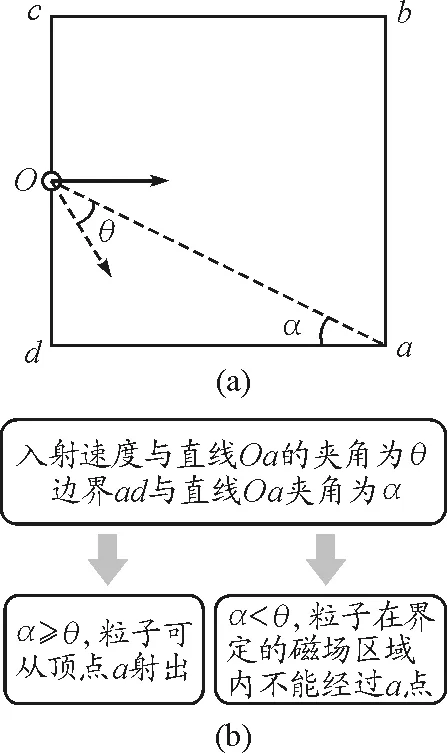
图2 判断粒子能否从a点射出的方法示意图
对于本题而言,根据几何关系可得
tan(θ+30°)=2
α>θ
因此选项A也正确.可以采用以下两种方法进行证明.
方法一:如图3所示,假定粒子从a点入射,c点出射,粒子入射速度方向与直线ac夹角为θ,对于直线边界而言,粒子以与边界成θ角入射,出射的速度方向也与边界成θ角(已在图3中标出).通过改变矩形磁场边界cd与直线ac的夹角α,可得到,若α<θ(如图3边界cd′所示),粒子必然经过边界cd′线之外,即在边界限定的区域内粒子不可能经过c点,若以最大速率偏转且不离开磁场边界,则必然会与cd′边界相切;若α≥θ,磁场区域“足够大”,不影响粒子在边界内的偏转,粒子必然可以从c点射出.
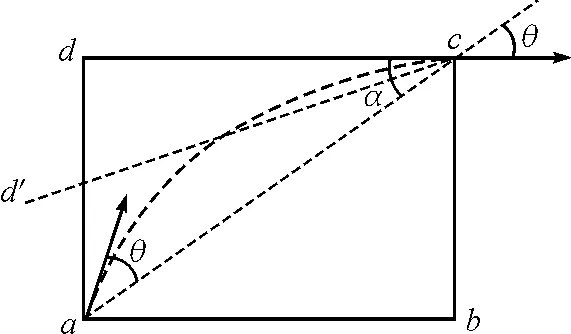
图3 方法一示意图
方法二:假设粒子先和dc边界相切,如图4所示,根据粒子偏转的对称关系可得,圆心角β=2θ,cd边是轨迹的切线,则切点e与圆心的连线必然垂直于cd边,通过几何关系可以证明,粒子经过e时所对应的圆心角φ=α+θ,由于经过e点后才经过ac边,因此β>φ,进而α<θ;当α=θ时,粒子通过c点的同时与cd边相切,当α>θ时,粒子可以从c点射出.
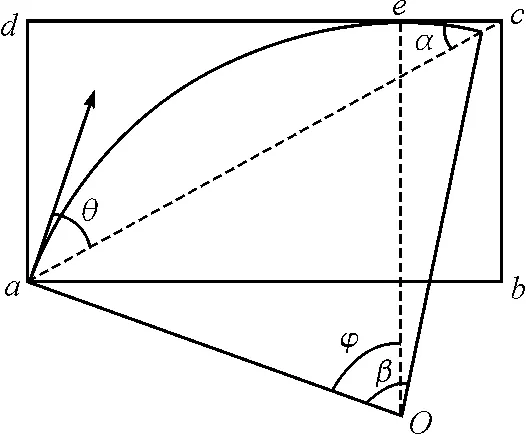
图4 方法二示意图
3 举例
通过角度的比较判断粒子能否经过边界顶点,可以简化判断步骤,节省判断时间,也能够简化思路更加准确快速地得到相应问题的结果.笔者对2019年高考全国卷Ⅰ中带电粒子在匀强磁场中的运动问题进行了改编,采用这一方法可以快速解决.
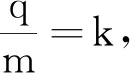
(1)若粒子刚好经过O点,求粒子的入射角度范围;
(2)若磁场的方向垂直纸面向里,粒子源可以沿着y轴移动,且能够垂直于y轴发射速度足够大的粒子,试问粒子源在哪些位置发射粒子时,粒子能够通过P点.

图5 高考改编题示意图
分析:对于这一问题,如果采用“伸缩圆”的方式分析,需要分析讨论多种情况,需花费较多时间.但若采用根据角度判断粒子能否通过某一点的方法,就简便很多.
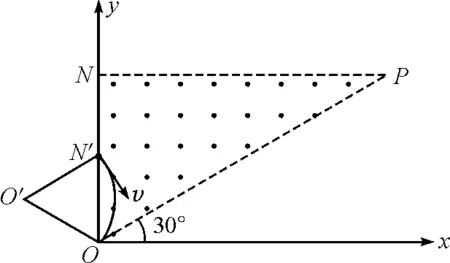
图6 第(1)问示意图
图中O′为粒子偏转的圆心,由于半径与ON′相等,则△OO′N′为等边三角形,因此∠O′N′O=60°,速度方向与y轴负方向成30°角.根据粒子在匀强磁场中的运动规律可知,粒子若通过O点,其速度方向与y轴负方向间的夹角必须不大于∠NOP,因此粒子的入射角度范围为与y轴负方向成30°到60°角.
对于第(2)问,粒子的速度足够大,偏转过程中可以先不考虑粒子的速度问题.根据粒子的偏转规律,先连接N′P,如图7所示,速度方向与N′P的夹角为θ,N′P与边界OP的夹角为α.若粒子经过P点,必须要求α≥θ,又因为
α+θ=30°
得到
θ≤15°
即
∠NPN′≤15°
于是
点N′的位置起始坐标为
所以,点N′的坐标yN′范围是:0.55d≤yN′ 图7 第(2)问示意图 以上内容,仅是笔者对这一问题的粗浅认识,不足之处,望请读者批评指正.
