“四点共圆”突破关联运动中的难点

周耀虎

(合肥一六八中学 安徽 合肥 230601)

关联运动一直是高中物理学习中的一个重点与难点，在两个及两个以上物体的运动问题中，关联速度的分析尤其重要，是学生学习中的拦路虎和易错点，具有典型性．正确建立连接体间的速度关联关系，是求解连接体有关速度问题的切入点，也是求解有关连接体综合问题的关键．

1 经典错题分析原因

【情景】如图1所示装置，两辆小车以相等的速率v0向相反的方向对称地牵引物体，求此时(轻绳于竖直方向夹角为θ)物块的速度v．

图1 错误的速度分解

不少学生可能会这样做：按图1的形式将两个v0直接合成

(1)

得到

v=2v0cosθ

(2)

式(2)是一个错误的结果，那么错在哪里呢？

问题的关键在于，学生忘记力与速度的合成是有区别的：物体运动对两根绳子产生的效果是独立的，速度分解如图2所示.

图2 正确的速度分解

不管以哪根绳子分解，因为绳子长度不变，所以总有

vcosθ=v0

(3)

因此

(4)

2 一般情况探寻规律

【变式】如果两车的速度大小不相等，如图3所示v1>v2，两绳子夹角为α，求此时物体的速度大小和方向．

图3 合速度分解到左边沿绳和垂直于绳

由于两车速率不相等，所以物体的速度不再是竖直向上的，问题由之前的特殊情况变成一般情况，分析如下.

设物体的速度与左边绳子的夹角为θ，由于两根绳子总长度都不变，按图3方式把速度分解到左边沿绳和垂直于绳方向，得到

v1=vcosθ

(5)

同理按图4方式把速度分解到右边沿绳和垂直于绳方向，得到

v2=vcos(α-θ)

(6)

由式(5)和式(6)联立可

cosα+sinαtanθ

(7)

由式(7)解得

(8)

将式(8)化简得

(9)

将式(9)代入式(5)或式(6)均可得到

(10)

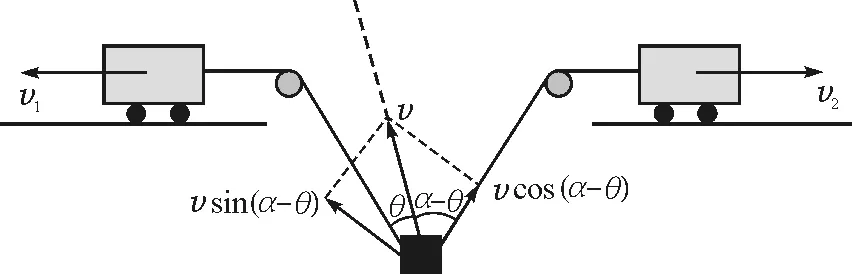
图4 合速度分解到右边沿绳和垂直于绳

如果每次都是这样分析，确实很麻烦，学生就算理解了，做起来还是不能得心应手，所以，我们可以把图3和图4合并为一个图，总结为：“四点共圆”，具体做法如图5所示.

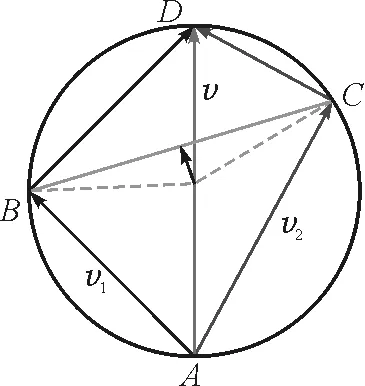
图5 “四点共圆”

设v1(AB)和v2(AC)的夹角为α，作一个外接圆，AB与BD相互垂直，AC与CD相互垂直，这两组均是沿不同绳子分解的速度分量，从图中可以看出合速度v的大小就是圆的直径AD的长度，我们只要求出圆的半径，就可以知道合速度的大小．

根据余弦定理可得

(11)

从圆心向BC作垂线，则等分BC，且BC与两半径组成的等腰三角形顶角的一半仍为α，由三角函数可求出圆的半径

(12)

由式(11)和式(12)联立可得合速度为

(13)

只要把上述作图的思路讲清楚，三步就可以求出合速度，学生以后再遇到类似问题不仅是懂了，更能快速地解出答案．

3 实战演练防止定势

突破了这类题，并不代表以后就不会错，平时要教育学生认真审题，要防止出现思维定势，下面再来看一道非常好的变式题.

【例题】图6为在平静海面上，两艘拖船A和B拖着驳船C运动的示意图．A，B的速度分别沿着缆绳CA和CB方向，A，B，C不在一条直线上．由于缆绳不可伸长，因此C的速度在CA，CB方向的投影分别与A，B的速度相等，由此可知C的( )

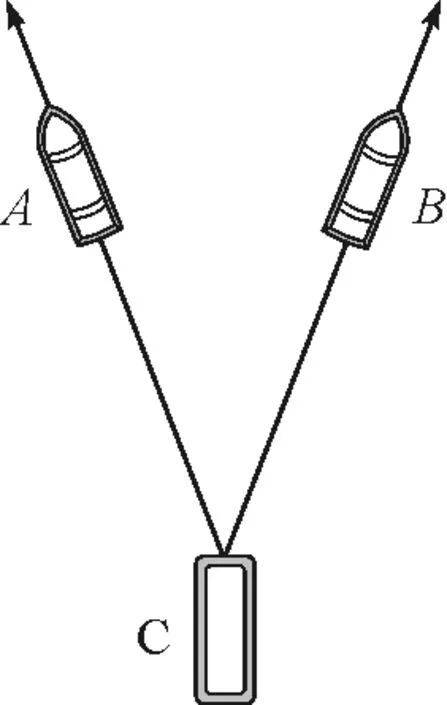
图6 例题图示

A.速度大小可以介于A，B的速度大小之间

B．速度大小一定不小于A，B的速度大小

C．速度方向可能在CA和CB的夹角范围外

D．速度方向一定在CA和CB的夹角范围内

这道题很容易按照思维定势误选选项A和C，但是由于船C的速度方向未知(不知道是往前走还是在转弯)，可能在AC与BC绳子之间，也可能不在AC与BC绳子之间，故两船速度大小无法比较，从本文之前的分析来看，船C速度的某一个沿绳分速度一定等于拖船A或B，则两拖船速度一定小于C船速度；故选项A错误，B正确.

由于船C的合速度方向未知，若在AC与BC绳子之间，就可以利用“四点共圆”算出合速度的数值

也可能不在AC与BC绳子之间，速度分解如图7所示，这时候就要注意与之前的区别了.

故选项C正确，D错误．

图7 合速度不在两绳间的分解

4 结论

通过上面问题的讨论，可以看出不要以为有3个矢量，就简单地认为其中一个就是另外两个矢量合成的结果[1]．物理教学应该教会学生从这类问题中的错误汲取经验，错不过三，为后期的学习与复习打下好的基础，这样才是真正高效的复习．