均匀带电半球壳轴线上的电场的深入研究及应用
2020-05-18徐远飞
徐远飞
(南京市南化第二中学 江苏 南京 210048)
1 存在问题
均匀带电半球壳问题可以看作是均匀带电球壳的电场特性的应用,对于一些特殊的位置可以采用填补法、等效法、对称性分析等方法,在理解均匀带电球壳的基础上,利用技巧解决半球壳的问题.
【例1】已知均匀带电球壳内部电场强度处处为零,电势处处相等.如图1所示,正电荷均匀分布在半球面上,Ox通过半球顶点与球心O的轴线.A和B为轴上的点,且OA=OB,C和D为直径上的两点,且OC=OD,则下列判断正确的是( )
A.A点的电势与B点的电势相等
B.C点的电场强度与D点的电场强度不相等
C.A点的电强度与B点的电场强度相同
D.在A点由静止释放重力不计的带正电的粒子,该粒子将沿AB做匀加速直线运动
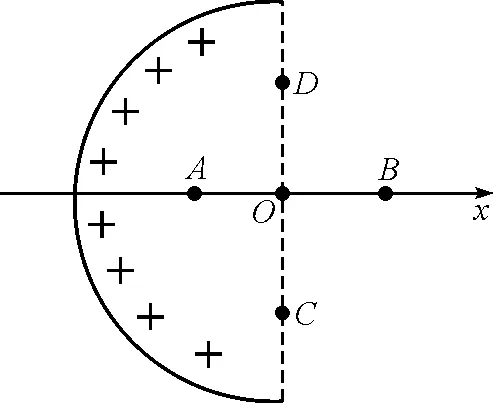
图1
例1是一个较为典型的均匀半球壳轴线上的电场问题.C,D两点的电势是否相等,可以用对称性来分析.对称性又叫不变性,外尔对此所作的定义是,如果我们对一件东西可以进行操作,使得操作后这件东西仍旧和以前一样,我们就叫这件东西是对称的[1].按照不变性定义分析,半球壳以x轴由C周旋转到D前后没有发生变化,可见C和D的位置具有对称性,C,D点的场强大小相等.
A,B位置显然对于球壳而言没有对称性,A,B点的电场强度大小该如何判断,可以使用填补法.将题中半球壳补成一个完整的球壳,且带电均匀,设左、右半球在A点产生的场强大小分别为E1和E2,根据均匀带电球壳内部电场强度处处为零的特性,可知E1=E2.根据对称性,左、右半球在B点产生的场强大小分别为E2和E1,且E1=E2.可以得出A的场强大小为E1,方向向右,B的场强大小为E2,方向向右,所以A点的电场强度与B点的电场强度相同.
由例1可以发现,我们可以通过技巧来解决一些半球壳电场相关问题,方法比较巧妙,但从另外一个角度来看,技巧偏重于解题,但是对于深刻理解均匀带电半球壳轴线上的电场的确切情况提供不了太多帮助,技巧可以解决部分特殊位置的定性判断,但是定性判断的准确性还是有必要从理论研究上得以保证.对于选项D的判断, 用分析很难得出带电粒子准确的运动情况.
笔者查阅了一些资料[2],发现有一些文章对于均匀带电半球壳轴线上的电场也进行了深入研究,但得出的结果仍然是限定在特定范围,结论不够完善.
2 均匀带电半球壳轴线上的电场的推导
2.1 均匀带电半球壳轴线上电场计算的基本方法
点电荷组所产生的电场在某点的场强等于各点电荷单独存在时所产生的电场在该点场强的矢量叠加[3],计算均匀带电球壳轴线上任意一点的电场强度,基本思路是应用静电场场强叠加原理.均匀带电半球壳具有轴对称性,由此可以推断半球壳的轴线上的电场在y轴上的分量相互抵消,场强方向必定沿着x轴的方向,如图2(a)所示.
设均匀带电半球壳的带电荷量为q,电荷面密度为σ,半径为R,在半球上取微元dS,dS在微元环L上,如图2(b)所示,可得出
dS=sinθR2dθdφ
dq=σsinθR2dθdφ
根据点电荷电场强度公式可得

图2 x>0时轴线上的场强分析
设P点距离O点的距离为x,根据图2(a)几何关系可得
r2=(x+Rcosθ)2+(Rsinθ)2=
x2+R2+2xRcosθ
微元dS对P的场强在x轴的分量为
(1)
对dEx积分可得
对此积分采用换元积分法,令
x2+R2+2xRcosθ=t2
球壳电荷量q与电荷面密度的关系
代入上式可得
2.2 均匀带电半球壳轴线上电场分段考虑及特殊点的计算
根据以上推导可得出轴线上离O点距离为x的点P的电场强度大小,分析式(1)可以看出,场强dEx的表达式与△BPD的几何形状有关系,P点的位置不同,得出来的dEx可能不同,积分上下限也有区别,导致积分所得的结果不同,因此要对P点的位置讨论,进行分段运算.
(1)x>0的位置已经推导.
(2)x=0时,有
kσcosθsinθdθdφ
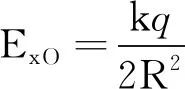
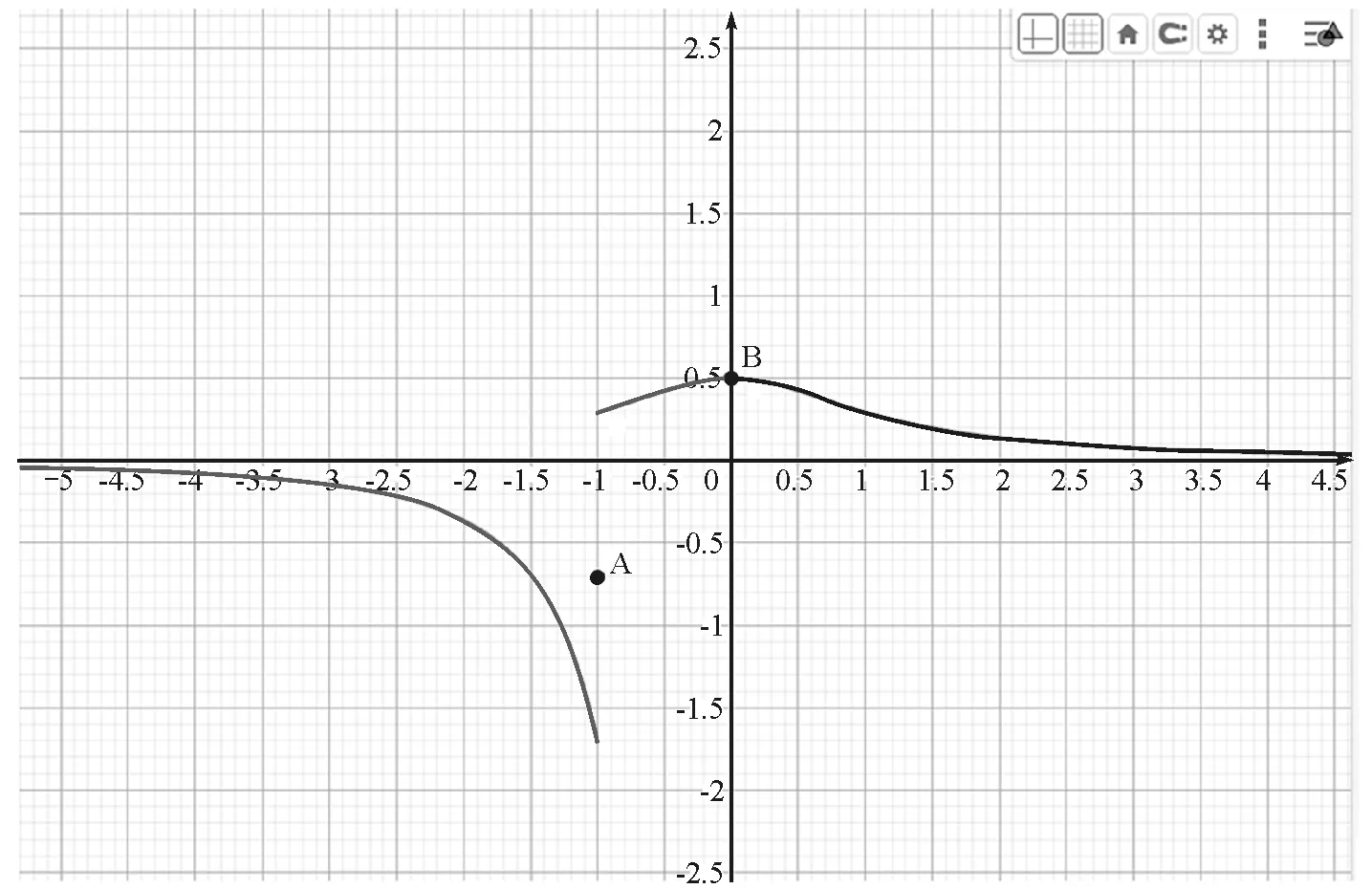
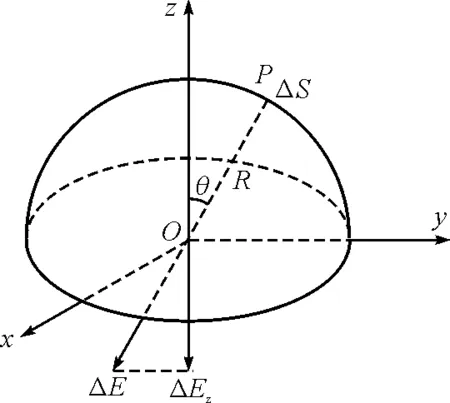
(3)当-R 图3 -R 由上式可以看出,在-R (4)当x=-R时,有 (5)当x<-R时,如图4所示,有 图4 x<-R时的场强分析 可得 同时,旅游者行为研究对象多以旅游活动类型为划分依据,涵盖广泛,涉及乡村旅游者、生态旅游者、出境旅游者、养老旅游者、女性旅游者、高铁旅游者、黑色旅游者、民族旅游者、自驾车旅游者、体育旅游者、智慧旅游者等诸多大类,呈现聚焦式、微观化的研究特征。其中,对于乡村旅游者、生态旅游者、女性旅游者的研究关注度最为集中,对于出境旅游者、高铁旅游者的研究则具有浓郁的新时代中国发展特色。此外,随着中国老龄化时代、智慧旅游时代的到来,未来国内旅游者行为研究的案例对象选择会向养老旅游者、智慧旅游者等新型旅游者拓展,深化对独特旅游者个体的微观专题化研究。 设沿着x轴的方向为正 综上得出均匀带电半球壳轴线上的电场强度为 用Geogebra软件生成函数图像,如图5所示,可以直观地了解轴线上场强的分布情况. 图5 用Geogebra软件生成的场强分布图像 通过计算可以发现,均匀带电半球壳轴线上的电场是比较复杂的,但是可以总结出一些结论: (1)以x轴方向为正,可以发现在x>-R的范围内,电场强度的方向都为正,在x<-R的范围,电场方向为负. (3)在-R (4)电场强度在A点的(x=-R)位置出现突变,电场强度方向沿x轴负方向,大小 【例2】均匀带电球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图6所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M,N两点,OM=ON=2R,已知M点的电场强度为E,则N点的场强为( ) 图6 例2题图 解析: 根据对称性可知左半球对N点的场强大小等于右半球对M点的场强,此题选项A正确. 方法二:将x=-2R和x=2R的情况分别代入推导出的公式进行计算 负号表示方向.根据题意可知 【例3】(竞赛)如图7所示,半径为R的均匀带电球面,电荷的面密度为σ,试求球心处的电场强度. 图7 例3题图 方法一:面元△S在O点产生的电场在z轴的分量为 式中ΔScosθ为面元在xOy平面的投影,由此可得 方法二:应用场强叠加原理直接积分得 通过对均匀带电半球壳的轴线上电场的深入研究,对轴线上的电场分布情况的理解更加全面,而不是停留在基于技巧的对特殊位置的片面理解,对相关问题的解释、教学、命题都有所帮助.
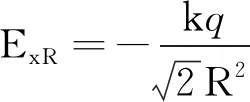

3 均匀带电半球壳轴线上电场分布的总结及应用

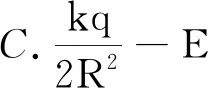
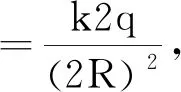

4 结束语
