利用两个结论巧解一道难题

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

瞬态过程具有很强的规律性，在物理学中的应用比较广泛.下面给出关于瞬态过程的两个结论，并用来解答一道有关“电容器-滑动杆”的瞬态电路问题.由此可对解题过程化繁为简，显得巧妙快捷.

结论1:对于一个瞬态过程的变量x=f(t)，设初始值为x0=f(0)，稳态值为x∞=f(∞)，时间常数为τ，若满足一阶常系数线性微分方程

则其通解为指数函数

即

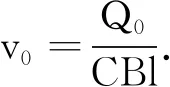
上述两个结论可分别称为瞬态过程的结论和电容器等效变换的结论.对于按指数函数规律变化的瞬态过程，只要推导出关于某个变量的一阶常系数线性微分方程的标准形式，得出3个要素，即可写出某个物理量随时间变化的关系式.对“电容器-滑动杆”瞬态电路问题的解答，可将电容器等效替换为一个滑动杆，对应3个参数，由此转换为双杆滑动的纯电阻电路问题，拓展了解题思路和方法.下面进行举例分析.

【例题】如图1所示，水平放置的光滑金属导轨，处在竖直向下的匀强磁场，磁感应强度为B，导轨间距为l，足够长，电容器的电容为C，金属棒ab垂直于导轨放置，其质量为m，电阻为R，导轨电阻不计.现有一个水平向右的恒力F垂直作用在棒ab上，设电容C足够大，求金属棒运动的速度和加速度随时间变化的关系式.

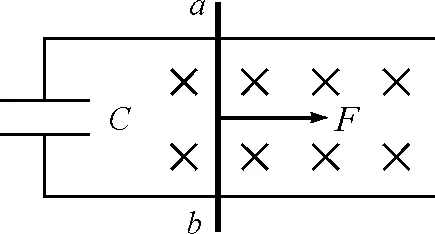
图1 题图

解析：金属杆在恒力作用下切割磁感线，产生感应电动势E=Blv，给电容器充电，电路中形成电流，使金属杆受到水平向左的安培力的作用.可将电容器转换为滑动杆a′b′，其电阻为零，初速度为零，质量m2=CB2l2，如图2所示，设右杆的质量m1=m.在t=0时刻，两杆都处于静止状态，设某时刻两杆的速度分别为v1和v2，产生感应电动势，因两个电源反向串联，且v1>v2，故整个回路的感应电动势为

e=Bl(v1-v2)

则感应电流为

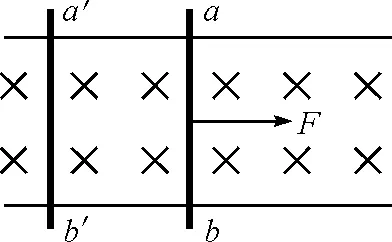
图2 将电容器转换为滑动杆a′b′

以向右为正方向，对左、右两个金属杆由牛顿第二定律分别列出微分方程为

对感应电流关于时间取导数为

联立可得

式中

设

则有

这是关于感应电流i的一阶常系数线性微分方程的标准形式.设i=f(t)，可知电流的稳态值为

时间常数为

感应电流的初始值为f(0)=0，由瞬态过程的结论可知方程的解为

由牛顿第二定律得加速度为

则相对速度为

对整体由动量定理有

Ft=m1v1+m2v2

两式联立得

将速度关系式对时间取导数也可得加速度关系式.

这就是如图1所示的“电容器-滑动杆”电路中滑动杆运动的速度和加速度.

速度关系式和加速度关系式还可分别变形为

这就是如图2所示的双杆在磁场中运动时主动杆的速度和加速度.

可见，当感应电流趋于稳态时，两个金属杆具有相同的恒定加速度，都将做匀加速直线运动.若m1=m2=m，则此时主动杆和从动杆运动速度随时间变化的关系式分别为

都随时间线性增大.

对于“电容器-滑动杆”电路，虽然感应电动势和电流都可趋于稳态，加速度也能趋于稳态，但滑动杆的速度不能趋于稳态.或者说，滑动杆先做初速度为零的变加速运动，经历时间为

后，将趋于匀加速运动，加速度为

对应的初速度即此时速度图像切线的纵截距为

虽然根据两个电路的等效性可以求出某些物理量，但要注意个别物理量是不同的，例如两个电路中的感应电动势不相等.