物理解题中的整体意识和局部意识*

张性海

(广州大学附属中学 广东 广州 510000)

在许多物理问题中，整体与局部的关系是普遍存在的.辩证唯物主义认为, 整体与局部是一对辩证的统一体，整体是指事物的全体或事物发展变化的全过程, 而局部则是指构成事物整体的各个部分及其发展过程的各个阶段，整体的特性是由各个局部及其它们的相互作用方式决定的, 局部总会以一定的形式或在一定程度上反映整体的性质.这些辩证关系为教学中处理物理问题提供了一个重要的启示, 即在解决物理问题时,应当善于从局部去认识整体, 从整体去认识局部，在思维上要训练学生处理问题的整体意识和局部意识，落实物理核心素养中科学思维能力的培养.笔者结合多年的教学实践, 谈一谈在教学中如何用整体意识和局部意识处理物理问题.

1 局部到整体的意识

既然局部是整体的局部, 它总会以某种方式为我们提供关于整体特性的某些信息.当事物从整体上看比较陌生, 而对它分解后的各个局部比较熟悉时, 我们可以从某一局部入手进行研究, 然后将这一局部的认识推广到另一相似的局部, 直至获得对事物整体的认识.

【例1】如图1所示，两足够长的光滑平行金属导轨倾斜放置，导轨左端接有耐压足够的电容器C，匀强磁场B垂直导轨平面，有一导体棒垂直导轨和磁场放置，可紧贴导轨自由滑动，导体棒和导轨电阻忽略不计.现导体棒由静止释放，电容器两端电压为U，导体棒加速度为a,试计算经过时间t时导体棒的速度大小v.

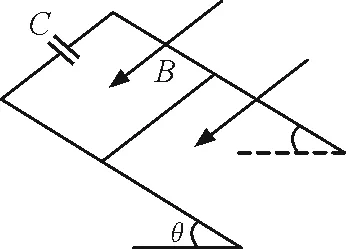
图1 例1题图

解析:本题要计算经过时间t时导体棒的速度v，就要判断导体棒是否做匀加速运动，但是导体棒的运动性质不明，如果全过程(整体意识)入手去处理，无法用现有的运动学公式计算v，为了使研究问题简化，可以在运动的完整过程中选一段微过程(局部意识)对应的时间Δt来研究.因为Δt很小，故可以认为在Δt时间内导体棒的加速度不变，对导体棒则有

Δε=BLΔv=BLaΔt

且电容器两极板之间的电压U和导体棒两端的电压相等，故

ΔU=Δε=BLΔv=BLaΔt

且回路中的电流

导体棒受到的安培力

F=BIL=CB2L2a

由

mgsinθ-F=ma

即

mgsinθ-CB2L2a=ma

可得

由a的表达式可见，a是常数，这表明导体棒是做匀加速直线运动，所以，经过时间t时的速度

小结:通过对导体棒某个微过程(局部意识)的分析，进而得出导体棒全过程的运动(整体意识)情况，窥一斑而见全豹，从整体和局部的关系出发，由局部去反映整体的解题思路.用局部意识分析问题时，要注意选取的“局部”具有“任意性”而非“特定性”，像本题中的Δt就是导体棒运动过程中的任一微时间段.

2 从整体到局部的意识

有不少问题, 虽然目标是探求某个局部的状态, 但若从局部入手, 会受到许多细节的干扰, 或容易使我们陷入片面性和局限性, “ 只见树木, 不见森林”.此时, 若改变角度, 从整体着眼, 居高临下, 由整体看局部, 则往往能看到各局部的地位作用及各局部之间的相互联系,由此对局部建立起正确、清晰的认识.

【例2】如图2所示，在水平地面正上方有范围足够大的匀强磁场.已知磁场的磁感应强度为B，方向水平并垂直纸面向里.一质量为m，电荷量为 -q的带电微粒从P点开始在此区域做速度为v的匀速圆周运动.初速度v与水平方向夹角为θ=45°,如图2所示,则为保证该微粒能做完整的圆周运动，P点的高度H应满足什么条件？(带电微粒的重力和空气阻力忽略不计)

图2 例2题图

解析:带电粒子在有界磁场中运动是一种常见的题型，也是学生普遍感觉到难度比较大的题型，究其原因，是因为他们很难画出粒子在有界磁场中的运动轨迹，也就无法进行相关问题的处理.如果换一个角度思考问题，在题设条件不变的情况下，把画带电粒子在有界磁场(局部意识)中运动轨迹(圆的一部分)，换为画带电粒子在无界磁场(整体意识)中运动轨迹(完整的圆)，然后再分析粒子在有界磁场中的运动情况，解题思路豁然开朗，难点迎刃而解，有一种柳暗花明又一村的感觉.如图3所示，给出了带电粒子在无界磁场中的运动轨迹，根据题设条件，在粒子轨迹图中标出P点的位置及速度v，如图4所示，根据题目要求可知，当边界(地面)在CD位置时，粒子刚好可以做完整的圆周运动，边界在CD下方时也可以做完整的圆周运动，在CD上方则不行.画出有界磁场的边界(地面)CD和P点到地面的最小高度H，根据

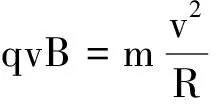
和

H=R+Rcosθ

可得

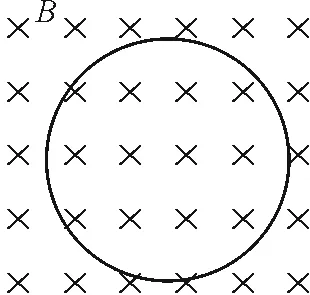
图3 带电粒子在无界磁场中的运动轨迹

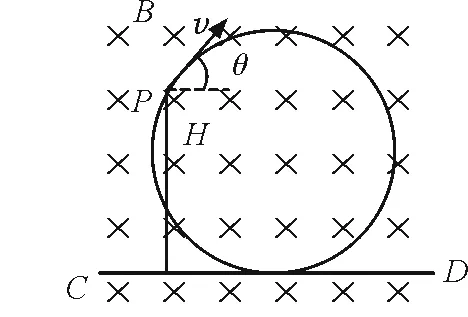
图4 粒子轨迹图中P点的位置及速度

小结:用整体意识处理问题，看问题时“站得高、望得远”，对问题的把握较为全面和完整.经常能从解题“困境”中打开思路，这种方法要求解题者对问题情景的全面性和状态的整体性有较好的理解和把握.

3 整体意识和局部意识的对立统一 有利于学生综合能力的培养

在许多问题处理的过程中，整体意识和局部意识的思路常常交替进行，不同的思路选用不同的方法，方法是解决问题的手段，方法的选择就是用整体意识和局部意识对问题的判断，而问题处理的过程就是学生能力培养和发展的过程.

【例3】如图5所示，倾角为θ，质量为M的斜面体静止在光滑水平面上.现有质量为m的物块，以初速度v0从斜面上某处沿斜面减速下滑.已知物块与斜面体间的动摩擦因数为μ，则在此过程中( )

A.斜面体向左加速运动

B.斜面体对物块做负功

C.地面给斜面体的支持力等于(m+M)g

D.物块和斜面体构成的系统水平方向动量守恒

图5 例3题图

解析:动量守恒问题涉及的是系统问题，是整体的问题，用整体意识处理，把m和M当作一个整体看待，整体水平方向合外力为零，则动量守恒，选项D正确.斜面体对物块做功的问题，研究对象是物块，可尝试先用局部意识的思路处理，对物块考虑动能定理

WG+WF=ΔEk

可知斜面体对物块做的功WF是负值，选项B正确.用整体意识的思路考虑m和M反而对选项B的正确与否较难判断.对选项A和C，如果用局部意识的解题思路，则对M的受力处理较为繁杂且费时，而把m和M看作一整体，用整体意识的思路考虑问题就简单很多.对m和M，水平方向由牛顿第二定律得

F合=0=max1+Max2

ax1水平向左，则M的加速度ax2水平向右，M向右做加速运动，选项A错误.对m和M，竖直方向由牛顿第二定律得

F合=N-(mg+Mg)=may1+May2

且ay1>0,ay2=0，则N>mg+Mg，选项C错误.

小结:是用整体意识还是局部意识的解题思路处理问题，需要尝试和判断，在尝试和判断中寻求最佳的解题方法，而且两种解题思路常常交替使用，互为条件，互为结果.

4 总结

学生在分析和解决问题时, 由于认知水平的限制，往往只注重物体或物理过程的局部, 而忽略整体与局部相互依存, 相互作用的关系, 不能从整体着眼、从全局去思考问题.有时则过于关注物体或物理过程的整体，而忽略从局部打开解题突破口的方法，面对题目，往往束手无策.教师在教学过程中要做个有心人, 在知识传授中，抓住契机对学生加以引导, 对整体与局部的关系进行归纳和总结, 让其成为学生思考和解决问题的一种习惯, 最终使学生分析和解决问题的能力得到提高.