Evaluating the Impacts of Using Different Digital Surface Models to Estimate Forest Height with TanDEM-X Interferometric Coherence Data

CHEN Hao HILL David A. WHITE Joanne C. CLOUDE Shane R.

①(Canadian Forest Service,506 Burnside Road West,Victoria,British Columbia,V8Z 1M5,Canada)

②(Applied Electromagnetics Consultants,26 Westfield Avenue,Cupar,Fife,KY15 5AA,UK)

Abstract:In our previous studies,we demonstrated the usefulness of TanDEM-X interferometric bistatic mode with single polarization to obtain forest heights for the purposes of large area mapping.A key feature of our approach has been the use of a simplified Random Volume Over Ground (RVOG)model that locally estimates forest height.The model takes TanDEM-X interferometric coherence amplitude as an input and uses an external Digital Surface Model (DSM)to account for local slope variations due to terrain topography in order to achieve accurate forest height estimation.The selection of DSM for use as a local slope reference is essential,as an inaccurate DSM will result in less accurate terrain-correction and forest height estimation.In this paper,we assessed TanDEM-X height estimates associated with scale variations in different DSMs used in the model over a remote sensing supersite in Petawawa,Canada.The DSMs used for assessments and comparisons included ASTER GDEM,ALOS GDSM,airborne DRAPE DSM,Canadian DSM and TanDEM-X DSM.Airborne Laser Scanning (ALS)data were used as reference for terrain slope and forest height comparisons.The results showed that,with the exception of the ASTER GDEM,all DSMs were sufficiently accurate for the simplified RVOG model to provide a satisfactory estimate of stand-level forest height.When compared to the ALS 95th height percentile,the modeled forest heights had R2 values greater than 80% and Root-Mean-Square Errors (RMSE)less than 2 m.For a close similarity in slope estimation with the ALS reference,coverage across Canada and open data access,the 0.75 arc-second (20 m)resolution Canadian DSM was selected as a preferred choice for the simplified RVOG model to provide TanDEM-X height estimation in Canada.

Key words:Interferometric COA;Digital surface model;Forest height

1 Introduction

Canada contains more than 347 million hectares of forestlands[1],distributed across vast regions that are largely inaccessible.Spatially-extensive,timely and cost-effective inventory and monitoring tools based on remotely sensed datasets are required to assess current forest status and track the impacts of disturbances across a range of ecosystems.One of the key attributes in forest inventories is forest height,an indicator of the timber production potential of a stand and closely related to forest biomass through allometric relations[2-4].

Airborne Laser Scanning (ALS)data has been widely used for generating spatially continuous forest height maps with high accuracy and spatial resolution[5,6].ALS metrics,such as the 95thheight percentile,co-dominant and dominant tree height,and top tree height[7-10],are efficient predictors of forest height and effective for standlevel measurements.Although national coverage of ALS data is common in some jurisdictions,ALS acquisitions are typically targeted over limited spatial extents,which does not generally allow for wall-to-wall forest height mapping over extensive areas,such as an area size of Canada’s forested ecosystems[11].

For large area mapping,forest height can be derived from optical and ancillary datasets through the upscaling of samples of height estimated from the spaceborne Geoscience Laser Altimeter System (GLAS)aboard ICESat[10,12,13],or airborne ALS transects[14].Alternatively,Beaudoinet al.Ref.[15]mapped a suite of 91 National Forest Inventory (NFI)attributes including forest height from MODIS imagery for years 2001 and 2011.However,such large-area approaches usually come at the cost of decreased accuracy and/or resolution that does not meet forest inventory requirements.

Previous research has demonstrated that interferometric coherence data from a single-polarization mode of the German TanDEM-X (TX)mission was sensitive to the vertical distribution of radar volume scatterers in forests and found it promising in mapping forest height in various forest environments[16-24].The application of TX single-polarization interferometric data generally requires inversion of a simplified version of the semi-empirical invertible scattering model,the Random Volume Over Ground (RVOG),to estimate forest height[19].This simplified model requires TX interferometric coherence amplitude data as input,as well as an external Digital Surface Model (DSM)to account for TX’s local angle of incidence on sloped surface at a pixel level.It does not rely on any true surface topography for height estimation,but estimates the height from an integral over distributed volume scatterers through the coherence amplitude in the vertical direction,which is different from other approaches as reviewed in the literature[25]where complex coherence,such as phase,is generally employed.

We applied the simplified RVOG model on TX interferometric amplitude data to derive forest height for different forest regions of Canada:the rolling foothills of Alberta (AB)[19],the mountainous terrain of British Columbia(BC)[20],and the relatively flat terrain of the Northwest Territories (NWT)[21].While the forest height results were relatively consistent for these varying topographic and forest conditions,a different DSM was used in each study.There are currently several medium-resolution (i.e.～30 m)candidate DSMs available at no cost and with nearly global/continental coverage,such as the Shuttle Radar Topography Mission (SRTM)DEM[26],the ASTER Global Digital Elevation Map (GDEM)[27],the ALOS Global Digital Surface Model (GDSM)[28],the Canadian Digital Surface Model (CDSM)[29],as well as others.

In this study,our objective is to examine and quantify the impact of using different DSMs as input into the simplified RVOG model for the Coherence Only Amplitude (COA)approach of deriving forest height,using independent reference data (ALS)for our assessment.In doing so,we provide an improved understanding of the impact of different DSMs on the estimation of forest height with the TX COA approach,and the characteristics of the DSM or DSMs that result in the most accurate height estimates.The results of this study can be used to inform the future use of the existing archive of TX single-polarization interferometric data,as well as similar future data sources for large-area forest height mapping.

2 Test Site and Data Sets

2.1 Study site -Petawawa Research Forest

Fig.1 Study site—the Petawawa Research Forest (red polygon),where forest stand polygons (pink)and field plots (red dots)are situated

The Petawawa Research Forest (PRF)is located～160 km Northwest of Ottawa and within the Great Lakes-St.Lawrence Forest Region,centered on 45.98°N and 77.50°W (Fig.1).Established in 1918,the PRF is over 10,000 hectares in size and contains both boreal and temperate forest species.The landscape is gently rolling with most topographic relief being less than 40 m and with a median slope value～4°,max～27°,and 90% of slopes <9°.The largest slopes appeared around the lakes of western site of the PRF.From east to west the soil composition varies from a sandy outwash plain,to glacial tills,to some localized thin soil over bedrock or bedrock outcrops.Ecological settings range from wetlands and riparian areas to uplands.Stand densities vary from open to dense,with age classes ranging from immature or mature.Forest stands are generally mixed.Many stands have a complex structure of species and age that are multi-storied[30].Based on 2012 ALS 95thheight percentile data,the height in the study area ranges from 2 m to 42 m with a mean/median height of～21 m.The PRF is home to more than 500 permanent sample plots and more than 2000 research experiments and demonstration plots,some of which have run over decades and designed to enhance forest management[31].

The PRF has been the site of numerous operational and experimental remotely sensed data acquisitions[32]that have played a critical role in the development of forest inventories.ALS data have been acquired and used with ground plot data to develop an Enhanced Forest Inventory (EFI)for the PRF[33].The plethora of available data sources at the PRF has results in the establishment of a remote sensing supersite,designed to enable the development,testing,and validation of algorithms and approaches for forest management[31].

2.2 Data sources

2.2.1 TanDEM-X interferometric data

The TX archive contains continuous and overlapping global coverage of TX Co-registered Single-look Slant-range Complex (CoSSC)data that were used to create a global DSM,also known as WorldDEMTM[34].A CoSSC image pair,collected over the PRF on April 21,2011,was provided to us by the German Aerospace Centre(DLR)as part of their science support program for evaluating CoSSC as an interferometric preproduct of the TX processing chain.This CoSSC data product has single polarization (HH)with a ground range resolution of 2.6 m and azimuth resolution of 3.3 m.The incidence angle at the scene centre is 42.6°.The CoSSC image pair was processed and co-registered by the DLR and the resulting interferogram was provided in slant-range geometry with an auxiliary file of range shifts used to co-register the image pair.The Height of Ambiguity (hoa)is nominally |43.9| m,which means the simplified RVOG model would have a useful dynamic range of～14 m to～43 m[20]for the PRF because the 2012 ALS 95thheight percentile data indicated a maximum height of 42 m and a mean/median height of～21 m.

2.2.2 Digital Surface Models (DSM)

The Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER)Global Digital Elevation Model Version 2 (GDEM V21https://asterweb.jpl.nasa.gov/GDEM.ASP)was released by the Ministry of Economy,Trade,and Industry (METI)of Japan and the National Aeronautics and Space Administration (NASA)of the United States in October,2011.ASTER GDEM V2[35]has a spatial resolution of 30 m and a horizontal datum of WGS84 (World Geodetic System 1984)as well as a vertical reference system of EGM96 (Earth Gravitational Model 1996).The coverage of GDEM V2 spans 99% of Earth’s landmass from 83°N to 83°S.

The Japan Aerospace Exploration Agency(JAXA)released the Advanced Land Observing Satellite (ALOS)Global Digital Surface Model V1.1 in March 2017.The ALOS GDSM,also known as the ALOS World 3D-30 m(AW3D30)[36],has a spatial resolution of 30 m and the same horizontal and vertical datum as ASTER GDEM V2.The GDSM coverage is from 83°N to 83°S.The ALOS GDSM is also open data,available for download from the JAXA Earth Observation Research Center website2http://www.eorc.jaxa.jp/ALOS/en/aw3d30/registration.htm.

The Canadian Digital Surface Model (CDSM)is part of Natural Resources Canada (NRCan)’s altimetry system designed to meet users’ needs for Canadian elevation data and products[29].The 0.75 arc-second CDSM (20 m)consists of derived products from the 1 arc-second (30 m)SRTM DSM and the Canadian Digital Elevation Model(CDEM)[37].The SRTM data was re-processed by NRCan with gaps filled using the CDEM to offer a complete coverage of the Canadian landmass.The horizontal datum is the North American Datum 1983 (NAD83)and the vertical reference system is the Canadian Geodetic Vertical Datum 1928 (CGVD28).The data were filtered to remove noise and aligned to the 0.75 arc-second grid resolution,and waterbodies re-flattened.The CDSM is open data,available for download from Natural Resources Canada3https://maps.canada.ca/czs/index-en.html.

The TX mission offers a global DSM,World-DEMTM.The commercial WorldDEMTMwith spatial resolutions of 12 m and 30 m were made available in 2017,but are not open and must be purchased from AIRBUS4https://www.intelligence-airbusds.com/worlddem/.The TX DSM data has a horizontal and vertical datum of WGS84 and EGM2008 respectively.The TX DSM at 30 m used for this study was provided courtesy of the DLR under their science support program for evaluation of TX DSM.

The DSM from the Digital Raster Acquisition Project for Eastern Ontario imagery(DRAPE)covers Eastern Ontario,Canada,and is freely available through Land Information Ontario5https://geohub.lio.gov.on.ca/.Leica ADS100 Digital Camera systems were used for the digital imagery acquisition,performed at 2,377 m above mean terrain to produce 20 cm orthorectified imagery and related products.The DRAPE DSM was then derived at 2 m from the digital stereo photography using the Leica GeoSystems software,XPro SGM[38].The horizontal datum is NAD83 with the vertical reference system of CGVD28.

2.2.3 Field plots,forest inventory and ALS data

In the summer of 2013,Temporary Sample Plots (TSP)were surveyed in the PRF as part of the Advanced Forest Resources Inventory Technology (AFRIT)program[39].A total of 223 circular plots were established and each had 14.1 m in radius (～625 m2).The plots were stratified based on forest conditions for the purpose of constructing area-based models with ALS data.The PRF Inventory was completed in 2007,using field data and soft-copy interpretation of stereo aerial photography.In total,there were 1193 forest stands delineated,with a suite of attributes interpreted.

Discrete-return ALS data with a point density of 14 points per m2were acquired on August 17,2012,covering～13,000 hectares including the PRF.LAStools software was used to derive a DSM at 1 m,as well as the 95thheight percentile metric (P95)at a 30 m pixel size.Following an area-based approach[33],a linear model,usingP95 and the stand height measurements from the AFRIT plots,was developed to estimate two measures of forest height at 30 m:Topht (averaged height of the thickest 100 stems/ha)and CDht (average height of Co-dominant and Dominant trees).The derived height models were then applied wall-to-wall for the PRF at 30 m.The ALS DSM and the resulting 30 m rasters forP95,Topht,and CDht were used as independent reference sources for validating stand-level TX forest height in the PRF.The AFRIT plot data,the PRF inventory data,and the ALS data/products are freely available for download through the National Forest Information System6https://saforah2.nfis.org/CSWClient/operated by the Canadian Forest Service,Natural Resources Canada.

3 Methods

Our height algorithm developed for the single-polarization TanDEM-X interferometric COA data was a simplified version of RVOG model derived from earlier studies in polarimetric interferometry[40,41].It estimates height locally by using an inverse SINC function as shown in Eq.(1)[42]

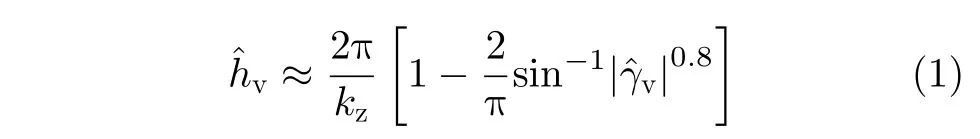
kzin Eq.(1)is an interferometric wavenumber,which is a function of a local angle of incidence and the normal baseline component of the interferometer as in Eq.(2)

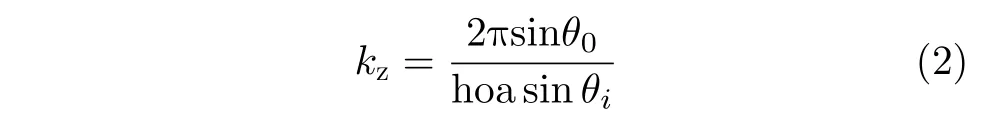
where hoa is height of ambiguity and θ0an incidence angle at scene centre,both of which were in TX metadata.θiis the variability of local incidence angle on sloped terrain and can be estimated from an external DSM at a pixel level.The interferometric wavenumberkzis what we focus on in this study to understand how local slopes derived from different DSMs would affect height estimation with a view to quantify any errors or limitations.

In general,we could use any available DSM.However,there were three key features to be considered.First was the spatial extent of a DSM used in application and its availability.Global or regional coverage with open access are preferred.Secondly,it was the spatial resolution of a DSM used to calculate the local slopes.We wanted a DSM with a spatial resolution that was commensurate with that of the target resolution of our final TX height product.Third,scale variations in different DSMs could have a potential influence onkzand then the accuracy of TX height estimation.If the terrain was relatively flat,a DSM may not be of great concern in overall model outcome,as Eq.(2)became to Eq.(3)

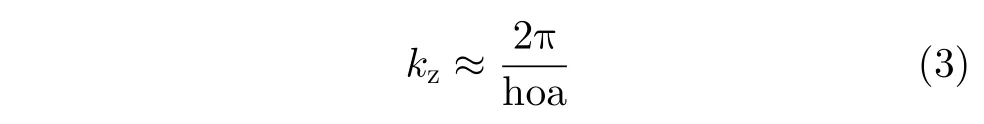
However,if areas contained large slopes facing either towards or away from the radar,DSM resolutions and accuracies would have a definite impact onkzand forest height estimation,as the local slope may be poorly estimated due to the level of residual errors associated with the DSM(Eq.(4))

Fig.2 and Fig.3 show a plot ofkzand a plot of height estimates respectively from Eq.(4).Here we pre-defined a baseline incidence angle as 42.6° (scene centre)in Fig.2.When the incidence angle increased or decreased about 4° (∆θ)from its true value θi,∆kzwould be～|0.018|,leading to the height estimate change～|1.7| m.The solid line in Fig.3,representing the average height of～21 m,had the coherenceset to 0.36.A DSM that would result in large changes inkzwhen compared to a more accurate baseline ALS DSM should be avoided.

To generate a TX forest height product,we estimatedwith a local averaging process using a boxcar filter with a 9×9 spatial window,reducing the variance and bias on coherence estimates,and then performed the aforementioned coherence compensations to the initial[19].Next we used the ESA Sentinel Toolboxes (SNAP7https://step.esa.int/main/toolboxes/snap/)and a chosen DSM to perform terrain-correction of the resulting slant-range imagein UTM projection(Zone 18)with a 30 m pixel spacing.During the same time,local incidence angles for all pixels were calculated forkz.Finally,a TX height map with a 30 m resolution was generated by applying Eq.(1).

Fig.3 Height vs.local incidence angle (coherence set to 0.36 for average height of～21 m)

We validated and compared the TX height maps derived from different DSMs within the PRF.Forest stands were defined by the 2007 forest inventory data,representing all plantation and natural forest stands within the PRF in polygons.Forest stand height was then extracted using the arithmetic mean of all the pixels in that stand.Because the ALS CDht and Topht were derived from both of ALSP95 and stand height measurements from the AFRIT plots,174 forest stands,containing the aforementioned 223 field plots,were located and considered as the initial pool of candidates for validation.

As the DSM datasets varied in data collection and release dates from 2000 to 2014,the 174 forest stands were first examined using high-resolution aerial photographs and Landsat images,acquired between 2000 and 2014,to assess if there had been any changes to these stands over the period considered.The forest stands that experienced change during this period were removed as the slope of a DSM would have been affected by any height change due to forest or vegetation removal.Stands less than two hectares in size were also removed because,at a 30 m resolution,the statistics used for assessment would suffer from boundary effects from larger surrounding stands.At the time of this study,DRAPE DSM was not available for the far west edge of the PRF,so the forest stands in that area were excluded.After the filtering,94 forest stands remained for validation of TX height estimates.

We used linear regressions (Eq.(5))to validate and compare TX height estimates,created within the 2012 ALS coverage,against the stand height maps derived from ALS metrics (hALS)

wheremandcare respectively the estimated slope and the intercept of the linear regression.

Eq.(6)is used to calculate Root Mean Square Error (RMSE),whereis the TX height estimation at theithstand,hithe height measurement from the ALS at the same stand location,and n the number of stands used to calculate the RMSE.AdjustedR2(here afterR2),the estimated slopem,and the interceptc,as well as the RMSE,were used to assess the level of impact of using different DSMs on the performance of the simplified RVOG model.

4 Results

Tab.1 shows the differences ofkzvalues for each of the DSMs when subtracting thekzimage derived from the 2012 ALS DSM over all 94 forest stands.The mean difference of thekzvalues indicated how different the average slopes were compared to the slope of the 2012 ALS DSM.Thekzgenerated from the CDSM had the best match with thekzfrom the 2012 ALS DSM with a mean differencekzof 0.0097.The worst match was the ASTER GDEM with a mean differencekzof 0.0435.

To showkzgenerated from the CDSM had the best match with thekzfrom the 2012 ALS DSM in all DSM candidates,we also show the histograms of eachkzfrom all 94 forest stands in Fig.4.Allkzstart at 0.1 and end with 0.2.Thekzhistogram from the CDSM has a form that is much closer to thekzfrom the 2012 ALS DSM.Thekzhistogram from the ASTER GDEM has the least similarity with a wider shape when compared to the 2012 ALS DSM.In this way we gained much needed insights on the potential influence of different DSMs as input into the simplified RVOG model.

We further examined each of the 94 forest stands to determine the cause of the maximum difference inkzvalue varied from that of the 2012 ALS DSM.The largest differences in thekzvalues were found in two forest stands that were adjacent to a water surface.In the processing of 2012 ALS DSM,water surfaces were masked out and given a value of 0.When it was resampled to the 30 m spatial resolution to producekz,these 0 values dominated and skewed the statistics of adjacent stand polygons.We also found several other forest stands that contained large differences inkzvalues.These maximums were mainly caused by boundary effects of flat open surfaces that were adjacent to the forest stand polygons.

The means of thekzdifferences and the distributions of thekzvalues were used to identify which DSM most closely matched the slopes generated from the 2012 ALS DSM.The CDSM had the lowest mean difference inkzvalue (0.0097)for all 94 forest stands and the most similar distribution ofkzvalues relative to the 2012 ALS DSM.According to Fig.3,a differentkzvalue～|0.018|would result in a difference in an estimated local incidence angle～|4|°,at which the height variation would be～|1.7| m.To minimize the errors introduced by a DSM in the simplified RVOG model,we should choose the CDSM for the local slope estimation.

Fig.5 and Tab.2 shows the height comparisons from the 94 forest stands.The TX heights estimated using the CDSM,ALOS GDSM,and DRAPE DSM showed the similar statistics inR2(～84%)and RMSE (～1.8 m)when compared to the 2012 ALSP95 height.The TX height estimates resulted from the CDSM had anR2of 84.1% and low RMSE of 1.73.When compared to ALS CDht in Tab.2,the ALOS GDSM had a higherR2of 88.5% followed by the CDSM with anR2of 87.3%,but the CDSM had a smaller RMSE (3.12 m)than the ALOS GDSM (3.18 m).For the Topht comparisons in Tab.2,the results were similar to the CDht comparisons.

Here we show that the CDSM,ALOS GDSM,and DRAPE DSM had very similar performance in height estimation with anR2of～84% and RMSE <2 m when compared to the ALSP95 height over the 94 forest stands that were considered relatively unchanged during the time period between 2000 and 2014.The use of a 2 m resolution DRAPE DSM did not have a marked impact on the height estimates compared to the use of a 30 m resolution DSM due to the resamplingprocess for the final TX height product at 30 m.In thekzimages,the 30 m DSMs captured similar large-scale topographic features,whereas thekzfrom the 2 m DRAPE DSM showed more fine topographic characteristics around the lake edges where large slopes were found,which translated into slight localkzvariations.

Tab.1 kz differences when comparing to kz generated from 2012 ALS DSM

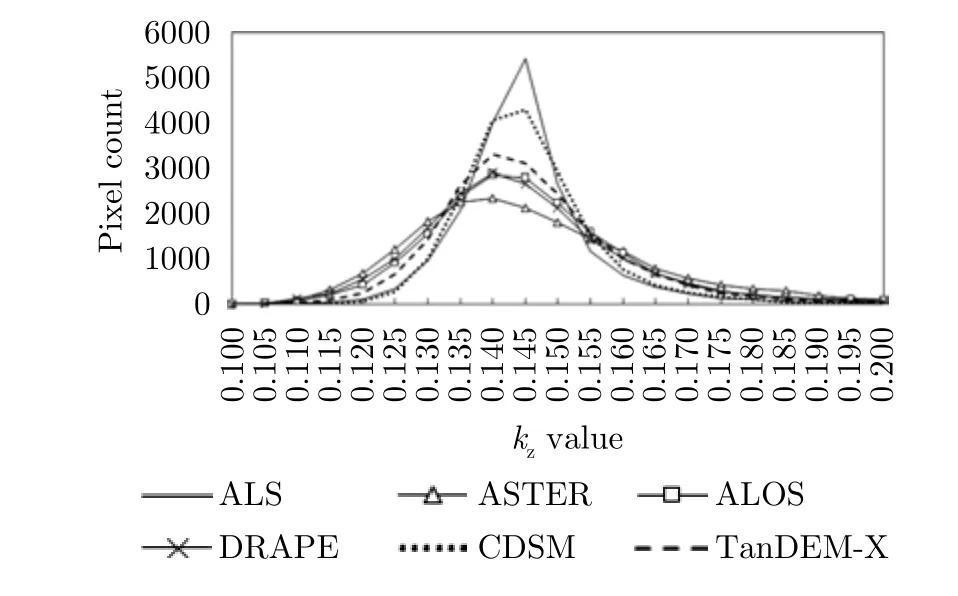
Fig.4 Histograms of the kz values for each candidate DSM and the reference data (2012 ALS DSM)

5 Discussion

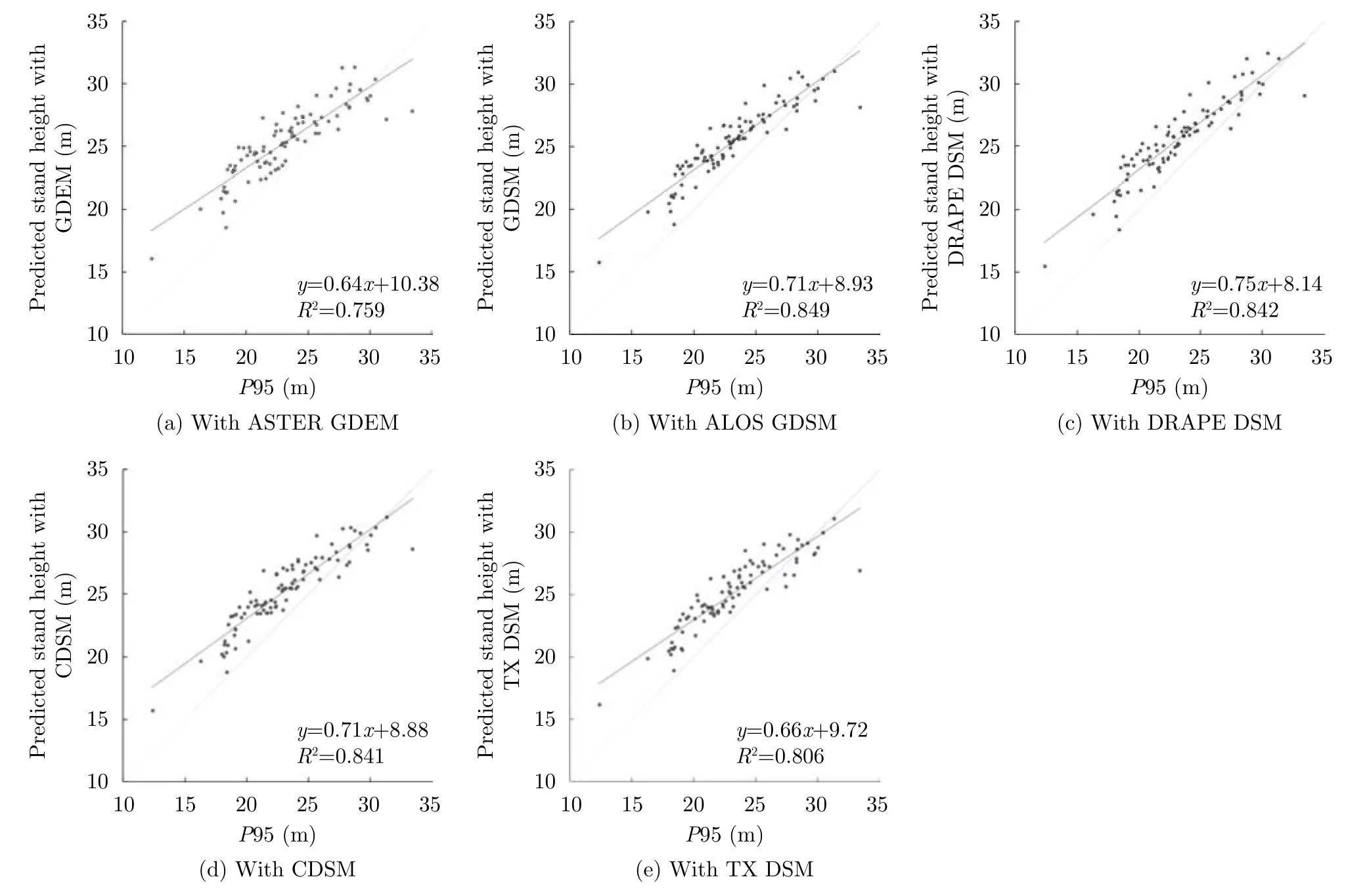
Fig.5 Observed ALS P95 height on x-axis and predicted stand height on y-axis

Tab.2 Height comparisons from 94 forest stands

These comparisons were made in the PRF area featuring relatively rolling terrain,which dominates most of northern boreal landscapes in Canada.The height validation results were consistent with those obtained over our northern boreal site in the NWT with anR2of 88% and RMSE of 2.7 m,where the CDEM was used in the model[21],and over highly stocked boreal forests in AB with anR2of 85% and RMSE 2.9 m,where SRTM applied[19].For forest height estimation in areas of rigorous topography with tall and dense temperate forests,for example in rugged mountainous forest regions of BC,Chenet al.Ref.[20]used the provincial TRIM DSM[43],similar to the CDSM,in the model to obtain anR2of 74% and RMSE 5 m and found that slopes were severe enough that small errors in slope estimation may lead to large height estimation errors.To mitigate the effect of slope variability in such challenging topography,a technique of using multiple baselines of TX CoSSC data should be considered[20].However,even though the PRF has moderate terrain and a DSM choice might not be expected to be as critical as for mountainous areas,our results still show that choosing a proper DSM would make a difference in final TX height estimation.

There is a confirmed bias in TX height estimates using the simplified RVOG model as revealed by linear regression’s coefficients,i.e.the slopemand interceptc,and the RMSE measures in Tab.2.We found a consistent overestimation of height from TX (especially at lower tree heights).There were two possible reasons for this overestimation:the lower part of the height dynamic range was overestimated due to the loss of sensitivity in the SINC function (Eq.1)as discussed in Ref.[20],and/or potential ground scatter in lower height stands was causing surface effects[42].Fig.5(a)- Fig.5(e)indicate an overestimation of approximately 3 m for 20 m trees.The bias may vary in different regions.It was also confirmed that forest cover types had an impact on the height estimates[21].When expanding the COA approach to other forest regions,the bias and possible influences of differing forest types require further investigation.Normally,we use the linear model (Eq.(5)),calibrated from ALS height measurements or other independent height sources (i.e.field plot measurements),to make an adjustment tom(close to 1)andc(close to 0).The coefficients for the baseline of 2012 ALSP95 in Tab.2 showed a slope～0.7 and an intercept～8 m for the CDSM,ALOS GDSM and DRAPE DSM in the PRF.We did not perform the linear correction in this study because our objective was to assess the relative performance of the different input DSMs and determine which DSM would provide the optimal solution for mapping forest height over large areas with TX CoSSC data.

Please note an external DSM used in Eq.2 to calculate local angle of incidence θiis one of the essential factors in the COA approach and its conversion to TX height.A key part of the DSM evaluation is the estimation of θithrough the calculation ofkzto determine the quality of the DSM.Selecting a quality DSM can certainly help with topography compensation and reduce errors in final TX height estimates.Another essential factor causing the RMSE can be the estimation of the interferometric coherenceused in Eq.(1),due to pixels with low SNR or high noise floor.This noise is uncorrelated between the image pairs and should be reduced as much as possible because it can cause decorrelation and loss of coherence in the interferogram.We have seen in our previous studies[19-21]that SNR corrections made a major difference in the level of estimated TX interferometric coherence and improved the final height estimation.Thus,proper coherence compensation procedures forshould be considered and performed in order to reduce the overall error level in RMSE.

There is another possible source of error in TX coherence estimation due to baseline decorrelation because of local topography.It follows from the fact that each point on the earth is viewed from slightly different angles at either end of the baseline.Although the transmitted radar spectrum is common to both receiving signals,its projection onto the earth is slightly different,causing a spectral shift that depends on local slope.In principle,this effect can be compensated by applying range spectral filtering[44].Since TX CoSSC data is by default range-spectral filtered as part of DLR’s basic SAR processor to remove such effect,users don’t have to implement such a scheme in their data process unless obvious inaccuracy found in the CoSSC data due to local slopes.

The TX COA approach is in contrast to other similar approaches using TX CoSSC data for forest heights,where phase information from complex coherence is utilized[18,24].The advantage of using phase is to have two parameters per pixel for height estimation,but generally requires auxiliary data for true surface location underneath the forest.For example a Digital Terrain Model(DTM)from ALS is needed in order to use phase for forest height estimation.The TX COA approach is free of such requirement,permitting large area mapping in regions,where such true surface information is unavailable.However,the main concern is the aforementioned bias in height estimates,which requires small ALS patches or ALS transects or ground plot measurements for final height product calibration.

6 Conclusion

In this study,we assessed the relative performance of several different DSM candidates used in the simplified RVOG model to estimate forest height with TX single polarization CoSSC data in the PRF.Candidate DSMs were selected for their spatial extent (i.e.global or regional coverage),open data policy,and spatial resolution.The assessment of the DSMs was conducted by generating the interferometric wavenumberkzusing different DSMs,and comparing each againstkzderived using the 2012 ALS DSM.The results showed that the CDSM,ALOS GDSM,and DRAPE DSM had similar performance in height estimation with a mean difference ofkz,0.0097,0.0332 and 0.0360 respectively,sufficient for the simplified RVOG model to produce TX height maps at 30 m withR2values greater than 84%and RMSE less than 2 m when compared to the 2012 ALSP95 height metric at the forest stand level.The use of the CDSM resulted in the lowest difference ofkzat 0.0097 in all 5 DSM candidates,indicating that the mean local incidence angle estimated from the CDSM differed by less than 4° overall,when compared to the 2012 ALS DSM.Slopes are related to the derivative of a DSM and,if all other criteria are met,the priority of selecting a DSM should be given to the one with a better spatial resolution than the coherence data,but as demonstrated herein there is minimal gain in using a DSM with a very high resolution,such as provided by DRAPE (2 m)for example.Since the CDSM covers all of Canada’s terrestrial area,offers open data access,and has higher spatial resolution of 20 m,if TX single polarization CoSSC data or other similar data were to become openly available,there could be great potential for large area mapping of forest height in Canada using the interferometric COA approach.

Acknowledgments

We acknowledge the financial and research support from the Canadian Forest Service of Natural Resources Canada and the Canadian Space Agency under Multisource Biomass GRIP (IMOU 13MOA41003).We further acknowledge the DLR for the provision of TanDEM-X CoSSC data and TanDEM-X DSM under XTI_VEGE6648 and DEM_FOREST0962 respectively.