以“课前自主学习”培养学生创新能力——基于自主学习型数学课堂研究

江苏省常州市湖塘实验中学 韦建华

创新是指人们为了发展需要，运用已知的信息和条件，突破常规，发现或产生某种新颖、有价值的新事物、新思想的活动。创造性思维是思维活动的高级过程，是在个人已有经验的基础上，发现新事物、创造新方法、解决新问题的思维过程。《国务院关于深化教育体制改革的意见》指出，在培养学生基础知识和基本技能的过程中，要强化学生关键能力的培养。要培养学生的创新能力，激发学生好奇心、想象力和创新思维，养成创新人格，鼓励学生勇于探索、大胆尝试、创新创造。

“不愤不启，不悱不发”。学生只有经过思考有所体会再开导，才能更好地理解知识、掌握技能；学生只有经过冥思苦想，又想不通时再启发，才会更加主动地聆听。现代“建构主义”认为，对事物的理解不是简单由事物自己决定的，事物信息要被人理解，这依赖于个体原有的知识经验，不同人的理解常常会因此而不同。学习是一个建构的过程，是学习者通过新旧经验相互作用来形成、丰富和调整自己经验结构的过程。真正的学习是学习者自主学习的过程。

我们将学生自主学习分为课前自主学习、课中自主学习和课后自主学习。这三个自主学习环节在教学过程中环环相扣、相辅相成。下面是苏科版七年级上册第6 章第3 节，“余角、补角、对顶角”课前自主学习导学案。课堂教学以此为基础引发下文，依次展开。

一、教材导读

请同学们阅读课本第159 页，回答下列问题：

1.将两块三角板①②如右图摆放，∠α 与∠β 的度数之间有什么特殊关系？请写出来：______。

2.固定三角板②，让三角板①绕其直角顶点O 在纸上转动，且在转动过程中两块三角板不能有重合部分。在转动过程中，∠α 与∠β 的大小变了吗？______。在（1）中发现的∠α与∠β 的度数之间的特殊关系还成立吗？______。

3.思考：怎样的两个角互为余角？

4.符号语言：

∵∠α+∠β=90°

∴∠α 与∠β 互余

反之也成立：

∵∠α 与∠β 互余

∴∠α+∠β=90°

5.思考：怎样的两个角互为补角？尝试写出相关符号语言。

符号语言：

∵_____________

∴_____________

反之也成立：

∵_____________

∴_____________

二、自主检测

1.填表（表一）

∠α 60° n°（0 ＜_____________n ＜90）∠α 的余角 35°∠α 的补角 140°

2.已知∠α 与∠β 互余，若∠α比∠β 大40°，则∠α=____，∠β=____。

3.若∠1+∠2=90°，∠1+∠3=90°，那么∠2____∠3（填“＞”、“=”或“＜”）。

4.仿照例1 完成：已知一个角的补角是这个角的余角的4 倍，求这个角的度数。

5.在下图（图1，图2）中分别画出与已知角∠α 相邻的补角，与已知角∠β 相邻的余角，根据所画图形提出一个相关的问题，并进行解答。

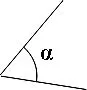
图1

三、通过自主学习，你有什么收获、疑问或感悟

（一）依托自主学习任务，启发学生建构基础知识、基本技能，夯实“创造”的基础

“发现问题、提出问题是创造的开始，解决问题是创造的过程，让我们在发现问题、提出问题、解决问题的数学创造中遨游。”课堂开始，建议采用适当的激励性语言，营造良好的学习氛围。

在上课过程中，要结合课前学生自主学习的内容，引导学生发问、发现，归纳总结，帮助学生进一步理解掌握基础知识。例如：本节课开始，结合自主学习，对学生可以提出问题：“两个角满足什么条件时互为余角？两个角满足什么条件时互为补角？”通过这两个问题，建构余角、补角，互余、互补的定义。

在上课过程中，要结合学生完成的课前自主检测题目，质疑提问，归纳总结，帮助学生进一步掌握基本技能。例如，根据上述课前自主检测第3 题，提问：“若∠1+∠2=90°，∠1+ ∠3=90°，那么∠2= ∠3，为什么？”预设同学们可能出现两种回答：“因为∠2=90°-∠1，∠3=90°-∠1， 所 以∠2= ∠3”或“因 为∠1+ ∠2= ∠1+∠3，所以∠2=∠3”。这两种回答都应予以肯定。一种是等量代换思想，另一种是等式的基本性质，它们是几何演绎推理的逻辑基础，是几何推理学习的基本技能。在此基础上，再归纳出“同角或等角的余角相等”性质。然后，通过类比，得出“同角或等角的补角相等”性质，理解掌握余角、补角性质。

通过学生课前初步学习教材、尝试解题、思考理解，学生已经建立了部分知识技能的经验基础，但有的还比较模糊。在教师提问，激发学生提问，生生、师生互助解决问题的过程中，学生加深了对基础知识的理解。通过课堂交流辨析，学生已有的知识技能变得清晰和丰满。依托学生课前自主学习，点拨启发学生建构知识技能，交流辨析，归纳总结，夯实了“创造”的基础。

（二）依托自主学习任务，引导学生尝试提出问题、解决问题，培养学生创新意识和能力

课前自主学习任务是学生数学基础知识、基本技能建构的载体。另外，设置课前自主学习任务，在掌握“基础知识基本技能”需要的基础上，还需要有学生感悟和发现的问题铺垫，以激发学生的好奇心。从而启发学生的探究意识，培养学生的创新意识和能力。比如第1 题，第5 题。

∠α 60° 55° 40° n°（0 ＜n ＜90）∠α 的余角 30° 35° 50° 90°-n°∠α 的补角 120° 125° 140° 180°-n°

如表二，可以提出问题：“通过自主学习检测的第1 题的解答，你有什么发现？”“你能提出怎样的问题？”如果学生不能发现其中的规律特征，不能提出有价值的问题，教师可以继续启发学生：“从同一个角的余角和补角的大小关系来看，你能发现什么规律特征？”在学生课前思考解题，已经初步感受理解问题的基础上，教师进行提问拓展，引导学生探究得出新的结论，从而培养学生创新的意识和创新能力。

在下图（图3，图4）中分别画出与已知角∠α 相邻的补角，与已知角∠β 相邻的余角，根据所画图形请你提出一个相关的问题，并进行解答。

角是几何图形，而且余角、补角的定义性质，今后主要结合几何图形进行运用和数学实践。例如：上面自主检测第5 题。学生通过动手操作能够进一步感受余角、补角的几何意义。同时，部分同学能够提出一些有价值的问题，并进行解答。对图3，有同学提出：“∠1 与∠2 大小有什么关系？为什么？”“∠3 与∠α 大小有什么关系？为什么？”这就为补角的性质“同角的补角相等”提供了有益的实践素材，渗透了数形结合思想。在此过程中，学生体验了创新和创造。再看图4，有同学提出：“∠AOD 与∠BOC大小有什么关系？为什么？”同样为得出余角的性质“同角的余角相等”，提供了有益的实践素材。真实课堂上有时还会有意外的惊喜。当老师提出：“同学们还能提出怎样的问题？”一时，教室里鸦雀无声，稍作等待，有一位学生站了起来，提出：“∠AOB与∠COD 大小有什么关系？为什么？”听到这个，老师先是惊讶，然后无比兴奋！立即给与赞扬“很好！”“有谁能回答这个问题？”老师激动地继续提问……这个问题本身就是本节课要重点深度分析加以探究的内容，竟然一位学生提了出来！这种“创新”超出了老师的期待，老师的内心怎能不激动万分！

传统的教学，学生知道将要学习的章节内容，但具体“怎么学”，“通过什么来学”，学生不知道。一节课，既要记忆理解基础知识、掌握基本技能，还要在此基础上拓展提升，培养学生的关键能力和核心素养，常常头尾不能兼顾。基础知识要学习要巩固，基本练习要校对，基本技能要总结，既不能“少讲”，也不能“精练”，这样的教学难以摆脱“填鸭式”“灌输式”的教学藩篱。事实上，现在的教材融合了教育专家的智慧，也代表了先进的教学思想，学生通过完成“课前自主学习任务”，看、练、悟，就能够初步掌握基础知识和基本技能，可以节省一部分课堂时间用以深化学习。依托课前学生自主学习任务，铺垫课堂问题情境，课堂教师启发引导，逐层推进、生成课堂教学，在此过程中，学生得以体验创新和创造，提高创新意识和能力。