水下拖缆稳态运动的多目标优化研究

王冲霄，刘忠乐，文无敌，张志强，赵 苗

(海军工程大学 兵器工程学院， 武汉 430033)

水下拖曳系统，是一种广泛应用于海洋监测、海洋研究以及军事等领域的水下探测装置，在开发海洋的先进技术手段中，拖曳系统装备具有极其重大的意义[1]。线列阵是水下拖曳系统的一个关键组成部分，其水动力特性直接影响整个水下航行器系统的快速性、操纵性及稳定性，开展水下拖缆的水动力特性研究具有重要的理论意义和工程实用价值。近年来，基于响应面的优化方法已广泛应用在稳健设计和多目标与多学科优化设计的代理模型里[2]。这种近似模型技术是在初始数据集合基础上构造逼近目标函数和约束条件的方法，同时也为快速优化和敏感性分析提供了一种高效的解决方法[3]。本文针对水下拖缆，在王飞[4-5]的稳态运动求解和分析的基础上，引入多目标优化设计理论，将复杂求解方法所得结果进行回归处理，建立起拖缆尾端拖曳深度和首端张力的二次响应面模型，给出多目标优化算法下的Pareto最优解集，并分析了拖缆参数对尾端拖曳深度和首端张力的影响。

1 拖缆运动模型及数值计算

为简化讨论过程，本文仅讨论稳定海流下自由端拖缆的运动模型，其拖曳系统如图1。

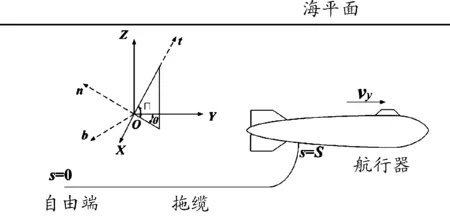
图1 拖曳系统示意图

其他的拖曳形式，例如尾端加载拖船、尾绳、水下拖体及其他的缆载设备，相比自由端仅在边界条件上存在区别，此处不详细讨论。将拖缆视为理想的柔性圆形缆绳，由水下航行器(AUV)搭载，建立空间固定的惯性坐标系O-XYZ，单位矢量定义为(i,j,k)，附着在拖缆上的局部坐标系btn，单位矢量定义为(b,t,n)。轴t表示拖缆切向，方向为缆长s的增长方向；轴n表示拖缆的法向，处在轴t和轴t在OXY平面内的投影所组成的平面内，并垂直于轴t；轴b与轴n和轴t共同组成右手笛卡尔坐标系。定义欧拉角θ，φ为拖缆微元相对惯性坐标系的姿态角，θ为Otn平面偏离OX轴的角度，φ为轴t偏离OXY平面的角度，θ∈(-180°,180°],φ∈(-90°，90°]，两个欧拉角均以逆时针方向为正方向。惯性坐标系和局部坐标系通过姿态角相关联，转换关系如下：

(1)

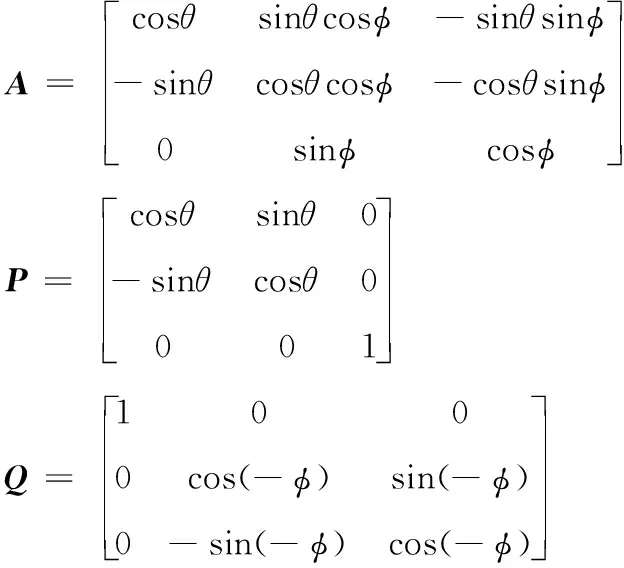
(2)

对于每个拖缆微元ds，在稳定直航的状态下，其重力、浮力、流体阻力的合力处于平衡状态，有以下平衡方程：

(3)

式中:T代表拖缆张力，始终指向拖缆的切向，B和G分别代表拖缆单位长度的浮力和重力，D代表流体阻力。

单位矢量(b,t,n)对拖缆长度s微分用“′”表示，则有[6]：

(4)

则可得：

(5)

所以张力在局部坐标系可展开为下式：

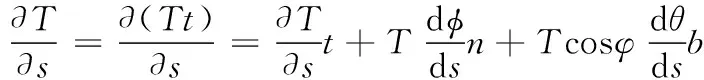
(6)

将式(6)与重力、浮力和流体阻力代入平衡方程式(3)中，并在拖缆局部坐标系下沿各坐标轴方向展开，则平衡方程写为如下标量形式[7]：

(7)

式中:w为拖缆单位长度在水中的质量，表示为：w=(u-ρσ)g，其中u为拖缆单位长度质量，ρ为流体密度，σ为横截面积，d为拖缆直径，ε为拖缆应变，Ct和Cn分别为拖缆的切向和法向阻力系数，ut，ub，un为局部坐标系下的速度分量，由系统相对于水流的拖曳速度转换到局部坐标系下得到，有：

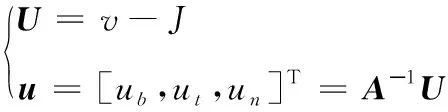
(8)

式中:v为拖曳速度，J为海流，仅有水平面内速度分量而无垂向分量。拖缆在惯性系下的坐标由下式给出：

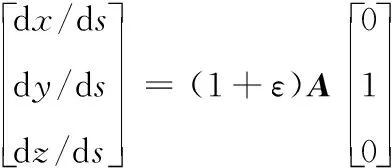
(9)

在均匀海流状态下，拖缆自由端即s=0处的张力和欧拉角变化率均为零，拖缆侧向无作用力存在，有θ≡const，此时可将稳态问题转换到二维空间下求解，在自由端的边界条件表示如下[4]：

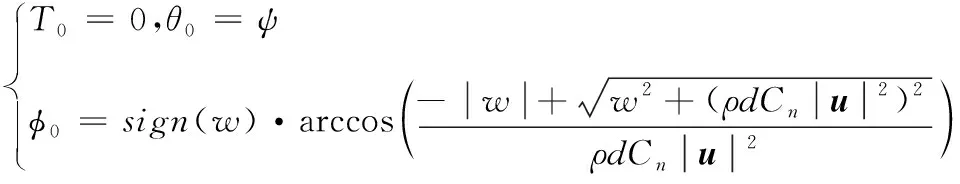
(10)

式中ψ为AUV的航行艏向角，将以上初始值方程和控制方程(7)、(9)联立，采用四阶龙格库塔方法进行积分计算，即可求出稳态解。

2 近似模型的建立

正常情况下，拖曳系统均工作于稳定状态，而稳态下的拖曳深度和拖缆首端张力是设计过程中两个非常重要的指标，拖缆的密度、杨氏模量、阻力系数以及拖曳速度和流体密度，均会对此产生一定的影响。王飞[5]对稳态拖曳各参数在一定的取值范围下，进行了拖曳深度和拖缆首端张力的初步研究，但每个参数的变化，是在其余参数不变的基础上进行的，而且最后仅对各参数对结果的影响进行了定性分析。以下将采用试验设计的方法，在王飞给出的拖缆模型基础上，构建参数和响应之间的近似模型，并得出尾端拖曳深度和首端张力的近似计算公式。

2.1 试验设计

本文选择拉丁超立方设计(Latin hypercube designs)作为试验方法。拉丁超立方设计方法是一种优秀的强调样本点分布均匀的试验设计方法[8]。该方法假设需要n个实验设计点，则设计变量会被分成n等分，在每等分中选择一个参数作为设计点。根据问题规模和复杂程度，样本点的个数也应该适当增多。通常情况下，对于5～10个变量的问题，样本点数量建议取为1.5×(n+1) ×(n+2)/2个[9]，因此针对本文的6个参数变量，选择42个样本点进行试验设计。拖缆模型和参数取值范围采用文献[5]给出的模型，参数如表1所示：

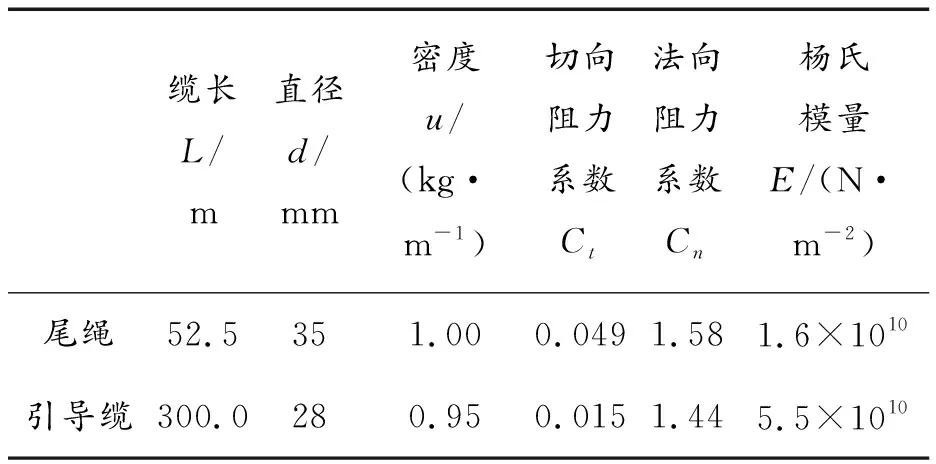
表1 拖缆参数

尾绳置于引导缆尾端，起到定深和稳定的作用。针对引导缆的物理参数以及流体密度ρ和拖曳速度vy设定取值范围如下：

108N/m2≤E≤1011N/m2

0.010≤Ct≤0.03

1.2≤Cn≤1.9

0.8 kg/m≤u≤1.2 kg/m

1 m/s≤vy≤3 m/s

1 020 kg/m3≤ρ≤1 030 kg/m3

2.2 二阶多项式响应面

二阶多项式响应面的数学表达式为：

(11)

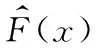
采用复相关系数R2作为响应面模型的误差分析指标，定义如下：

(12)

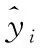
采用多项式回归技术对试验设计的样本点和响应值进行最小二乘拟合，并求出待定系数，构造出近似模型。回归模型表示如下：

yi=f(xi,θ)+εi，i=1,2,…，n

(13)

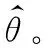
Z=33 539.7-258.38x1-2 728.3x2-1.26×10-9x3-

87.61x1x2-1.21×10-11x1x3+

0.19x1x4-27.43x1x5+12.28x1x6-

3.04×10-11x2x3-3.07x2x4+

121.57x2x5-0.47x2x6+1.22×10-12x3x4+

5.44×10-12x3x5-3.12×10-11x3x6-

0.19×10-3x4x5-0.21x4x6-52.96x5x6

(14)

F=-429 504.9-1 752.43x1-84 097.73x2-

9.14×10-9x3-842.3x4+3 016.54x5-

2.03x1x4-241.36x1x5+40.65x1x6+

3.1×10-9x2x3-52.68x2x4-5 144.58x2x5+

47 585.52x2x6+9.16×10-12x3x4+

5.12×10-11x3x5+1.54×10-11x3x6-

1.26x4x5+1.26x4x6-597.65x5x6

(15)

式中变量(x1,x2,x3,x4,x5,x6)分别代表参数中的Cn，Ct，E，ρ，u，vy。通过计算复相关系数来验证响应面模型的拟合精度。其中，Z的复相关系数为0.996 96，F的复相关系数为0.999 53。该响应面模型拟合程度较好。

3 多目标遗传算法

本文所探讨的是如何实现尾端拖曳深度最大、首端张力最小的多目标优化问题，则本优化问题的数学模型可以描述为：

minF, maxZ

findCn,Ct,E,ρ,u,vy

s.t. 108N/m2≤E≤1011N/m2

0.010≤Ct≤0.03

1.2≤Cn≤1.9

0.8 kg/m≤u≤1.2 kg/m

1 m/s≤vy≤3 m/s

1 020 kg/m3≤ρ≤1 030 kg/m3

(16)

大多数情况下，上式的各个子目标往往是互相冲突的，其中一个子目标的优化会带来其他子目标的损失，所以多目标优化问题的优化解是一个解集，称为Pareto最优解集，解集中的元素称为Pareto最优解，Pareto最优解集在目标函数空间中的像称为Pareto前沿。在目前流行的优化算法中，遗传算法最适合求解多目标优化问题的Pareto解集。本文采用遗传算法中的NSGA-Ⅱ算法，基于ISIGHT平台，完成整个优化过程。NSGA-Ⅱ算法利用基于Pareto支配的排序方法将个体进行分层排序，并通过计算拥挤距离的方式对同一层级个体进行具体排序，具有较高的运算效率和较好的收敛速度[10]。本优化问题的主要流程如下：

1) 初始化拖缆的二阶多项式响应面计算模型，调入所需参数，初始化进化过程的参数，并随机生成初始种群N；

2) 将初始种群N中的个体依次赋值给拖缆计算模型，修改待优化参数并运行该模型，输出对应的拖曳深度和张力值，判断是否满足约束条件，以惩罚系数来处理不满足条件的个体，使其在进化过程中被淘汰；

3) 对种群中所有个体均以此方法进行操作，得到对应的输出值，从而完成种群的初始化工作；

4) 对初始种群N进行非支配排序并计算拥挤距离，得出每个个体的优劣性指标；

5) 以t记录进化次数，初始值为1，对父种群Nt执行交叉、变异等进化操作，产生子代种群Na；

6) 对每个子代种群Na进行计算，得到对应目标值；

7) 对父代种群Nt和子代种群Na进行非支配排序并计算拥挤距离；

8) 对种群进行更新，对上一步骤合并的种群进行修正，得到新的种群Nt+1，判断是否达到最大代数，如果是则输出非支配解集，否则继续迭代。

4 计算结果

本优化过程的种群规模为24，遗传代数为50，交叉概率为0.9，所得深度和张力的Pareto前沿散点分布如图2，选取3个优化方案，方案1中Z最大，方案2中F最小，方案3位于中间，所得优化结果如表2所示。Pareto前沿为非支配解集，最终方案的选择依赖于实际情况和选择者偏好[11]。

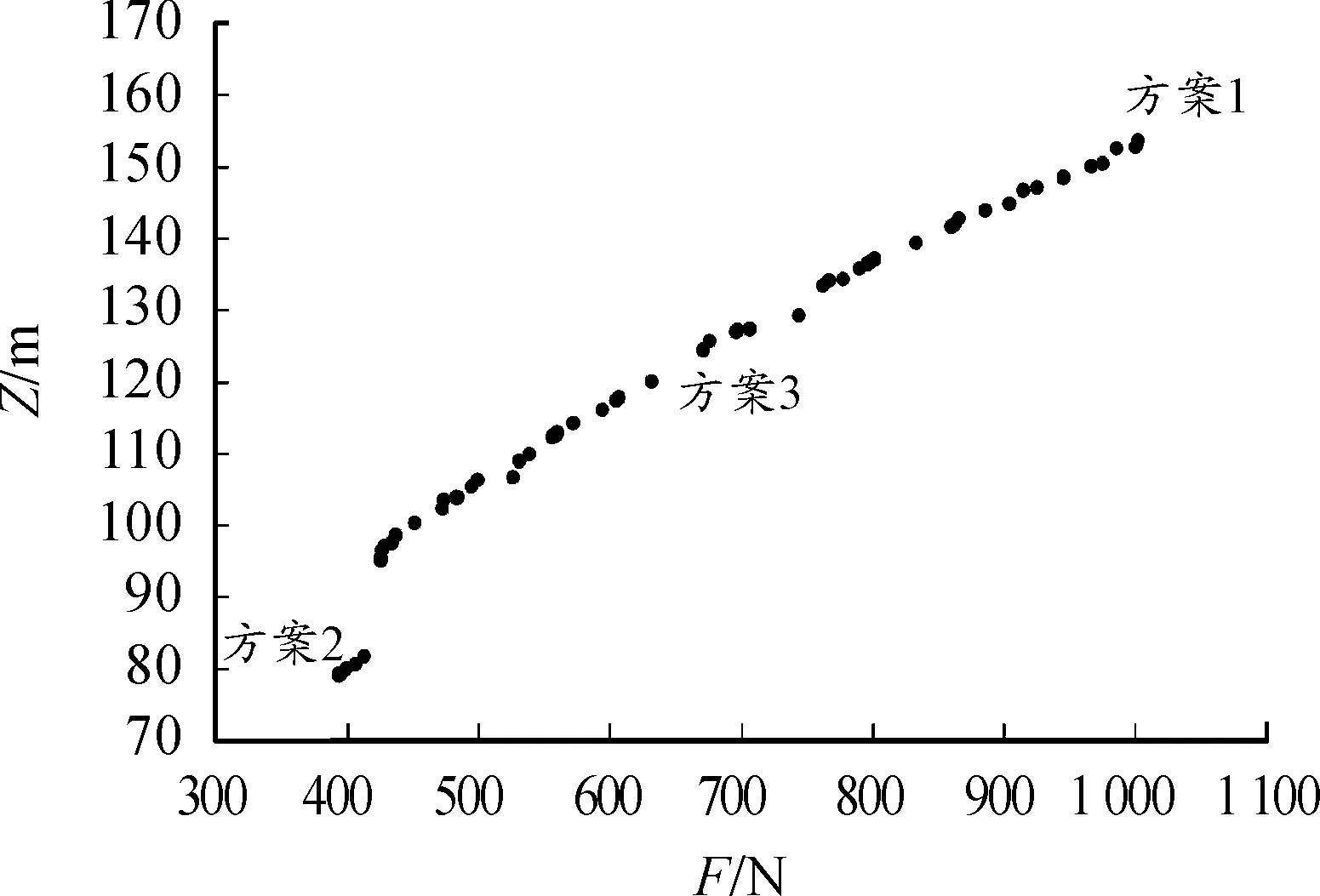
图2 拖缆优化的Pareto前沿散点分布

表2 Pareto解集中的三个优化结果

本文同时在ISIGHT平台上通过数据处理给出各参数对尾端拖曳深度和首端张力影响的Pareto柱状图，如图3和图4所示。图3的第一条、第三条和第六条以及图4的第四条和第六条表示该参数与响应呈负相关关系，其余表示该参数与响应呈正相关关系。可以看出，拖曳速度vy对尾端拖曳深度和张力的贡献程度百分比最大，分别达到了-52.53%和62.56%；其余各参数中，拖缆密度u和法向阻力系数Cn对尾端拖曳深度贡献程度百分比较大，分别为32.47%和-12.24%，切向阻力系数Ct和拖缆密度u对张力贡献程度百分比较大，分别为22.18%和12.12%，而杨氏模量E和流体密度ρ对两者的贡献程度均可忽略不计。以上分析结果基本和文献[5]所得结论一致。

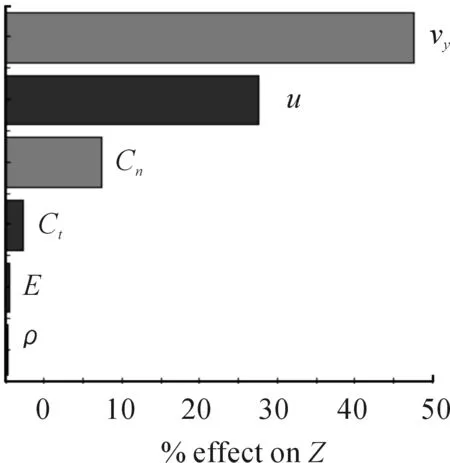
图3 参数对拖曳深度影响

图4 参数对首端张力影响

5 结论

基于ISIGHT平台实现了参数的多目标优化并得到Pareto解集，为设计者提供了重要的设计信息；通过计算各参数对尾端拖曳深度和首端张力的影响，验证了前人的结论。若拖缆模型和参数取值范围有变，本文所得出的尾端拖曳深度和张力的近似计算公式相应会发生变化。