空间自回归模型误差分布估计的渐近性质*

曾庆樊

(广西师范大学 数学与统计学院,广西 桂林 541004)

0 引言

随着经济的快速发展以及对数据的收集更加完整,在实际数据中,数据往往是具有空间关联性的,由此空间计量经济学受到许多国内外学者的关注.在理论研究与应用领域都得到快速发展.1973年Cliff和Ord[1]出版的Spatial autocorrelation首次考虑到了空间效应,提出了空间自回归模型;Anselin[2]于1998 年出版的Spatial Econ metrics:Methods an d Models对空间计量经济学理论做出了系统的整理.2004年LEE[3]证明了空间自回归模型拟极大似然估计的渐近性质;2010年Lee和Yu[4]建立了具有固定效应和空间自回归扰动的空间自回归面板数据模型的拟最大似然估计的渐近性质.

本文考虑如下空间自回归模型:

其中n为空间单位总量,X n=(x1,x2,…,x n)'是n×k固定设计自变量的观测值,Y n=(y1,y2,…,y n)'是n×1随机变量的观测值,W n=(w1,w2,…,w n)'是一个预先给定的n×n维空间权重矩阵,ρ∈R为自回归参数,β∈R k是参数向量,E n=(e1,e2,…,e n)'为独立同分布的随机误差项,其中e i具有未知的分布和密度函数f(x),且满足

ρ的对数似然估计为

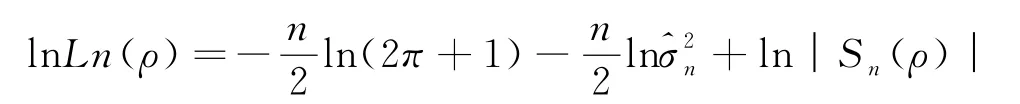
ρ的拟极大似然估计^ρn为上式极大化的值.

以往在对参数进行估计时,我们通常假定e i是服从正态分布的,但是在许多实际问题中正态性假定并不合理,此时参数估计的结果也并不理想.因此估计e i的未知分布和密度函数具有十分重要的意义.关于误差分布估计的研究并不多,柴根象[5]研究了线性模型误差分布估计的渐近性质.许冰[6]利用进一步一般化了柴根象的结果,定义了更广泛的f(x)的估计形式.杨瑛[7]研究了非参数回归模型误差分布估计的大样本性质.杨亚宁、赵选民[8]研究了半参数回归模型误差分布估计的大样本性质,在一定条件下证明了估计依概率收敛.本文将误差分布估计推广到空间数据模型上,研究了空间自回归模型误差分布估计的渐近性质,在一定条件下得到了f(x)的估计f^n(x)依分布收敛.

1 主要结果