基于雅可比矩阵下一种新的证券组合策略

任育泽

（成都理工大学，四川成都 610059）

关键字：组合证券；雅可比矩阵；函数相关

一、引言

众所周知，现代投资组合理论（MPT），以如何分配资金给不同资产来实现收益最大化和风险最小化作为核心问题，以构建投资组合模型来求解不同资产的投资权重作为常用研究方法，不仅是现代金融学的开端，也是现代金融理论的研究动力，无论在理论上还是实践上都具有重要价值。

MPT自Markowiz开创至今，发展了近70年，取得了众多成果。大体而言，现有成果主要集中在研究基于改进收益或风险测度的投资组合模型、研究非完美市场下的投资组合模型、研究多阶段投资组合模型，研究行为投资组合模型、研究投资组合在其它领域的应用等等。这些成果对发展和完善MPT具有重要作用，为进一步研究和应用投资组合模型提供了参考。

然而，尽管MPT获得了丰硕的研究成果，但现有成果扔存在着一些缺陷，其中最为主要的便是依靠单一的投资组合模型不能完全分散组合风险，以至于组合投资着仍有可能暴露在巨大的风险之下。

受启发于FOF基金，在证券市场上运用优秀的投资组合策略构建出组合证券，再从其中选出多支不具备相关性的来进行投资，如此势必能够在既定的预期收益下大幅度降低风险。

二、Markowiz投资组合理论

Markowiz的投资组合理论认为，由于投资组合的价值变化是一个随机过程，所以必须以它的均值来衡量收益，以它的方差来衡量风险。将资金分散投资于不同的证券之上，比全部资产都投在单一证券的风险低，狭义的投资组合理论就是寻找一个收益率一定情况下的风险最小的投资组合。将投资组合中各证券所投金额占总资金的比率作为变量，上述问题就可归结为一个线性约束下二次规划问题。

该理论的基本假设为：1所有的投资都是完全可分的；2一个投资者意愿仅在收益率的期望值和方差这两个测度指标的基础上选择投资组合；3投资者事先知道投资收益率的概率分布，并收益率满足正态分布的条件；4投资者更倾向于高期望收益和更低方差的投资组合。

为此Markowiz专门提出了均值方差模型来刻画风险，资产组合的方差包括每个资产的方差和资产间的协方差。证券收益率之间的关系可以用相关系数或协方差来表示，风险用收益率的方差来刻画，在n支证券(r1,r2,…,rn)下，上述内容可用数学语言可表示为：

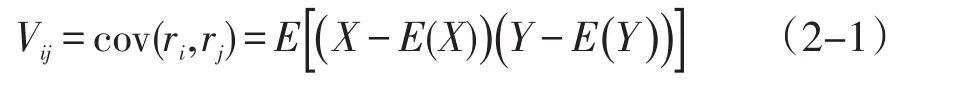
是ri,r之间的协方差，

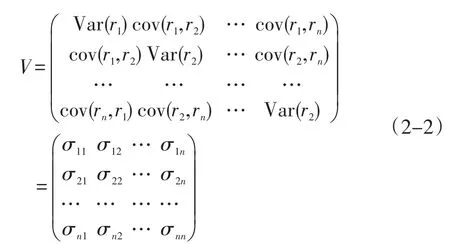
组合的标准差应满足

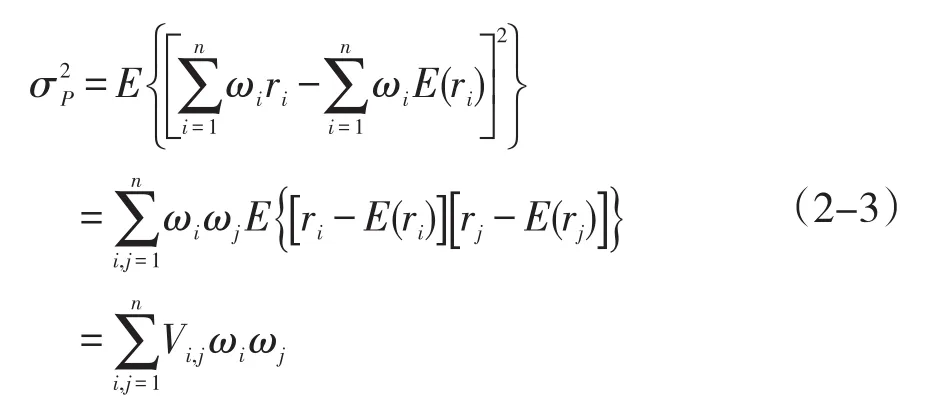
使用矩阵表示为

称 ωi(ω1,…,ωn)′为组合， μω=ω′μ 为组合的收益，σω=为组合的风险，这样均值方差证券组合的选择问题就变为

这是一个二次规划问题，不难看出，构成组合的证券收益率之间相关性越小，投资组合的风险越小。但是难点在于在当今的金融市场环境下，寻找不具备相关性的证券是极其困难的，甚至连它们是否线性相关，相关性有多少，仅仅依靠现有的手段，也很难做出具体的分析。也正因为此，该方法存在缺陷。因此，首先需要解决如下问题：1确立一种策略，保证在该策略下存在相关性为零的“证券”；2寻找一种判定方法，能够有效判断“证券”之间的函数相关性。

三、对组合证券的再组合

鉴于依靠单一的投资组合可能难以有效分散风险，从而有必要对投资组合进行再组合，以期进一步分散风险，提高投资组合的有效性。因此，下文提出一种新的策略来构建组合证券并利用雅可比矩阵进行甄别。

今假设当前存在n支证券(r1,r2,…，rn)，并针对这n支证券采用不同的投资策略，每一个投资策略会得到在该策略下最优的一个投资组合，我们称其为组合证券，这个组合的期望收益会是一个函数yi，这样就可以得到在自变量(r1,r2,…，rn)下的一个函数组

因为雅可比矩阵可以判定函数组的相关性，无论该相关性是线性的还是非线性的。所以此时，只要用雅可比矩阵来判定它们，便可以甄选出不具备相关性的组合证券，这在数学上显然是可行的。

但是此时该方法还有一个隐患，即是否对n支任意用不同策略构建的组合证券，它们之间的收益函数都是函数相关或者函数无关的。如果若是这样的话，本文所提出的这种方法将变得毫无存在的意义，因为根本没有判别的必要性。为此，首先证明该方法的存在性。

3.1 该测度方法的存在性证明

要证明的是，对n支任意用不同策略构建的组合证券，它们之间的收益函数既有函数相关的，也有函数无关的。欲证明该理论，必须要知道当函数组的雅可比矩阵表现为什么形式时才会代表函数无关或者相关。为了便于证明，此处以方阵为例。

假定因变量y1,y2,…,yn对自变量x1,x2,…,xn连续可微，而自变量x1,x2,…,xn对新变量z1,z2,…,zn连续可微，则可以得到因变量y1,y2,…,yn对新变量z1,z2,…,zn连续可微，且

若上式中z对y也是连续可微的，则由上式可知

显然它的系数矩阵就是n×n的雅可比矩阵，于是联立以此为系数行列式的线性方程组中能把dx1,dx2,…,dxn解出来，而且

其中t为线性函数。由隐函数存在定理可知，在y1,y,…,yn对x1,x,…,xn连续可微的前提下，只须

便足以保证 x1,x,…,xn也对 y1,y,…,yn连续可微。这样，连续可微的函数组便在雅可比行列式不等于零的条件下，在每一对相应点y与x的邻近范围内建立起点与点之间的一个一对一的对应关系，这就说明了yi之间不具备函数关系，否则x和y之间便不可能是一一对应的关系。

要证明的是，并非任意策略构建出的组合证券都是函数相关或者函数无关的。首先给出变量的定义：

①Y(y1,…,yn)：其中yi表示用策略i构建的组合证券的收益；②X(x1,…,xn)：其中xk是第k支证券从时间t=0到t=T这段时间的收益率，由于t=0的价格是已知的，而t=T的价格是一个随机变量，故而xk是一个随机变量； ③ωi(,…,)：用策略i构建的组合证券中对各个xi的购买比率，因此显然有+…+=1。

根据前文讨论，只需证明：

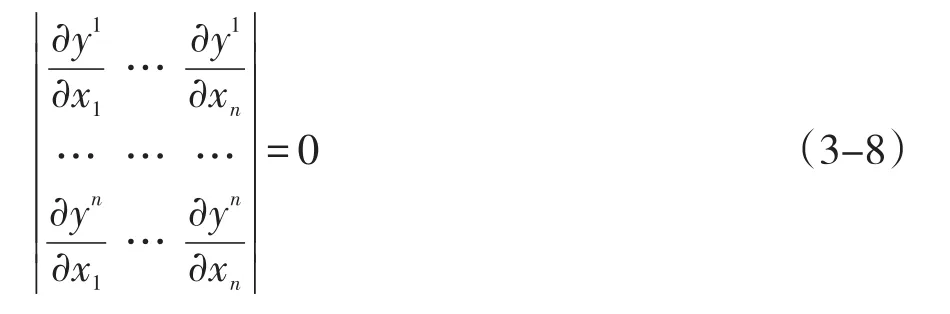
不成立或者

恒成立，则对任意D1,…,Dn，都能找到合适的 τ1,…,τn，且 τ1,…,τn不全部为零，有

可以写成

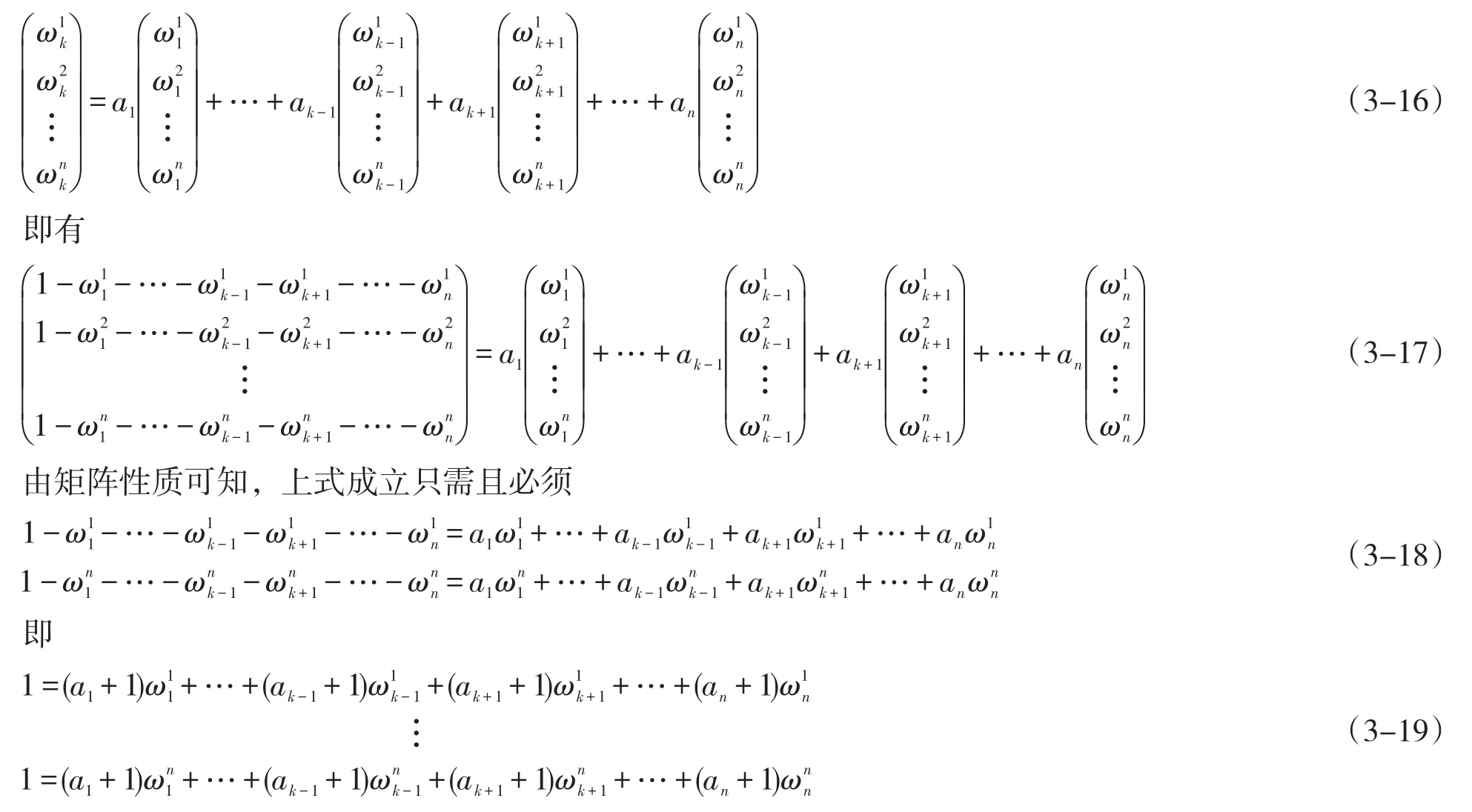
当其不为方阵时，需要证明的是矩阵的秩k=n，即只需要证明矩阵中有n个线性无关的向量，由上面的证明可知确实存在这种情况。

3.2证明该方法较一般的投资组合更有优越性

按照3.1的方法，总可以找出一组不具备相关性的组合证券 f1,f2,…,fm，其收益函数为y1,y2,…,ym，收益的协方差矩阵为

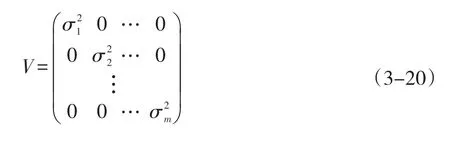
根据投资者的需求，运用投资策略作用于这一组组合证券，可以得到在第i支组合证券上的投资比例为 ωi(i=1,2,…,m)，且1=，其收益函数记为雅可比收益函数J=ωiyi，根据公式（2-3），其风险函数为+…+.需要证明的是，存在一组 ωi，使得}.这就说明这种新的投资策略存在这样一种可能，在相同收益的情况下，风险小于当前任意一种投资策略。

由收益函数的线性，显然有min{y1,y2,…,ym}≤J≤max{y1,y2,…,ym}.由于 yi是系列满足预期的收益函数，上下界之间不会有太大差距，这就说明J应该也是在投资者的预期收益区间的。

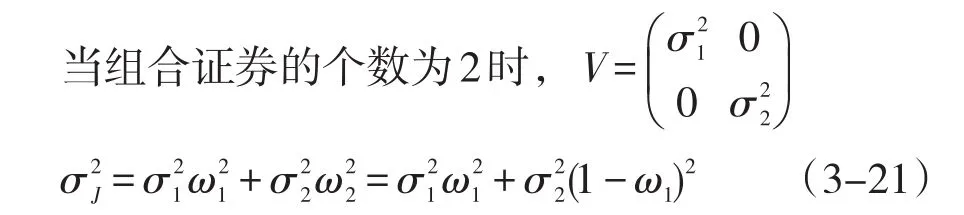
不妨令σ1<σ2，根据二次函数性质，容易得到结论

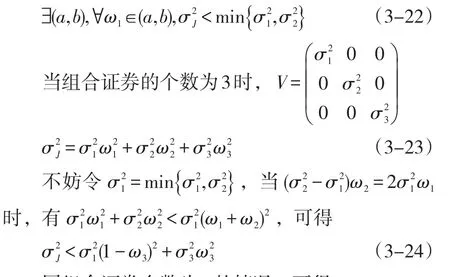
同组合证券个数为2的情况，可得

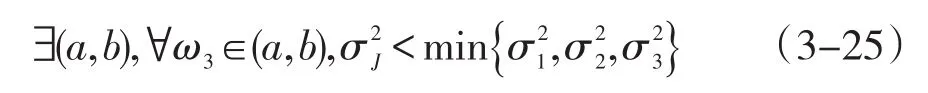
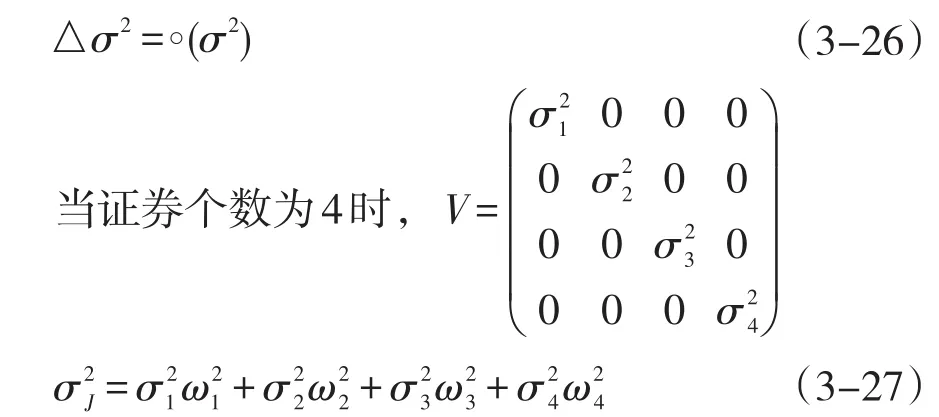
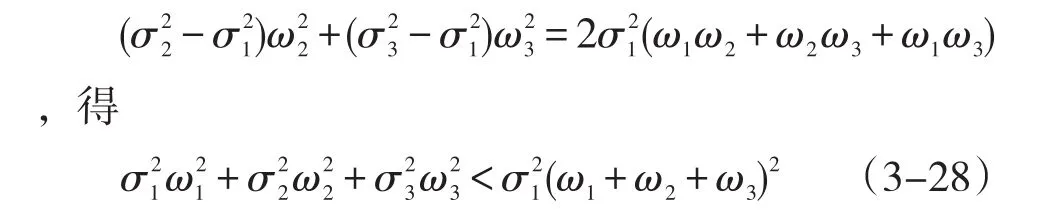
同组合证券个数为3的情况，可得

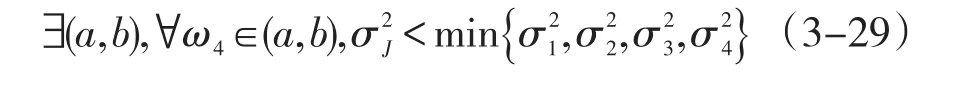
依次进行下去，由强数学归纳法，可以得到结论，在收益相差无几的情况下，新的投资组合可能比现存任意一种投资策略下的组合证券风险都低。

四、仿真算例

以上证行业指数的000032、000033、000036为例，从2016年11月4日到2018年7月23日，其期望收益率为μ=(0.75 0.84 0.85)T

收益率的协方差矩阵为

先以投资者追求最小风险为策略来计算它的最优组合下的收益率和风险。将数据带入公式（2-5），可以得到

在该情况下组合向量为

ω=(0.5472 0.0458 0.4070)T

可见最小风险为0.7667，此时的收益率为0.7948.

以对数效用函数为策略构建组合证券，将数据代入公式（见参考文献1）

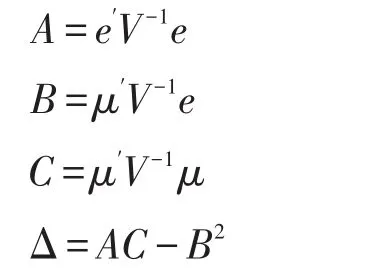
可得A=1.3102；B=1.0413；C=0.8460；D=0.0241.

带入

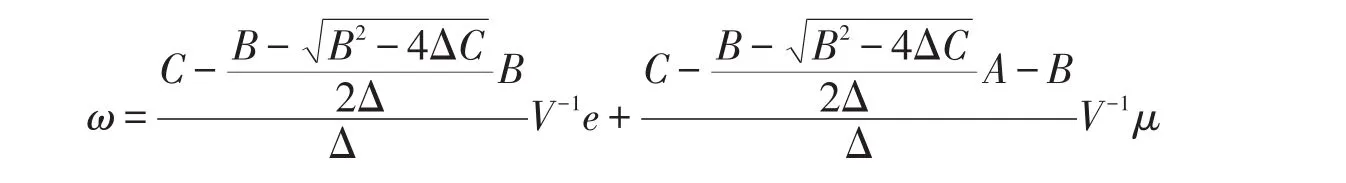
可得

ω=(0.381 0.184 0.435)T

在该策略下组合的风险为0.7918，期望收益率为0.8101.

以指数效用函数为策略构建组合证券，将数据代入公式（见参考文献2）

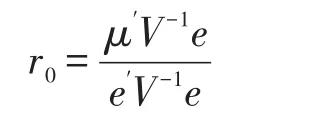
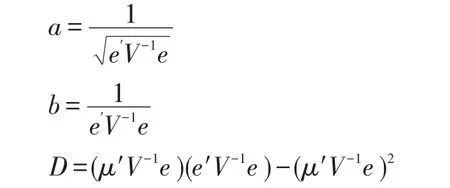
k为风险厌恶系数（大于零为风险厌恶，这里取k=4），进一步代入公式

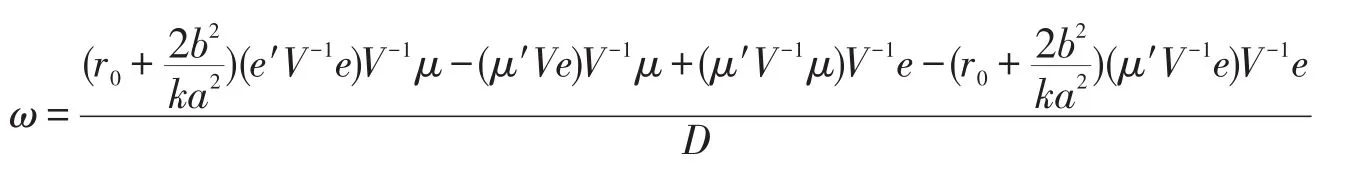
可得ω=(-3.6080 3.5064 1.0996)T

在该策略下组合的风险为9.4123，期望收益率为1.1740

以基于雅可比方法的投资组合理论求解，按3.1可知，收益函数的雅可比矩阵为

秩为2，所以组合证券函数无关，所以组合证券的协方差矩阵为

我们对这两支组合证券进行组合，令投资第一支组合证券的权重为w，有

σ2=0.7918ω2+9.4123(1-ω)2

当组合风险最小时，有ω=0.9224，最小风险为0.7303，期望收益率为0.8383.可以看出，如果单纯从风险和收益的角度来考虑，本文这种策略是效用最大的。

图1

五、结束语

尽管当前投资组合策略层出不穷，但是它们都未能克服Markowiz投资组合理论的局限性，即当前金融市场上证券之间相关性极高，线性相关不能刻画证券之间的相关关系等弊端。本文另辟途径，将组合证券和雅可比矩阵纳入到投资组合的研究框架，理论研究和实证结果表明，进一步降低风险，为克服证券之间相关性过高，相关性难以准确度量提供了可行路径，无论是在理论上还是在时间上都具有参考价值，不仅解决了这一系列问题，甚至从3.2的证明中可以看出，本文所提出的这一方法可以对任何组合进行再优化。