小学高段学生几何识图能力培养路径探析

李爱莲

[摘要]几何识图能力的培养不仅有助于指导小学高段学生学习几何知识、锻炼空间想象能力，而且有助于培育小学高段学生的图形信息搜索能力和数形结合能力。教师应通过转化、数形结合、小组合作等方式不断提高学生的空间观念与几何识图能力，进而培养其数学核心素养。

[关键词]小学数学;高段;几何识图能力;转化;数形结合

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）11-0032-03

《义务教育数学课程标准（2011年版）》中“图形与几何”板块主要包括四个方面，即图形的认识、图形的测量、图形的运动、图形与位置，目标是培养学生的几何直观和空间观念。几何识图能力的培养与“图形与几何”的课程内容有着密切联系，创新小学高段学生几何识图能力的培养路径，须进一步培养学生读图、析图、画图、用图的能力，从而提高学生利用数形结合解决问题的能力。

一、走进生活，提高读图能力

数学源于生活，但又具有一定的抽象性。空间与图形相关知识的教学要以学生的认知水平与经验为起点，为其形成良好的空间、抽象观念提供更多元、更丰富的感性素材。

教材中就有十分丰富的几何图形.教师教学时要注意数形结合，特别是在算术教学中指导学生观察图形、认识图形，通过模型或者图片参与到几何识图的过程中，从而感受到几何知识是对现实问题的抽象。例如，在讲解三角形具有稳定性时，先出示大桥图片，指出相邻两根斜拉索与桥面形成三角形;再出示校门口的伸缩门图片，学生观察得出组成伸缩门的基本图形是四边形，门可以伸缩，说明四边形是不稳定的;最后再举例生活中的桌子晃动问题，通过钉上木条，形成三角形，使桌子停止晃动。通过这些例子，使学生充分认识到三角形具有稳定性的特性。

教师也可以指导学生多方位、多角度地对照、观察、识别各种实物、模型、直观图，从而了解并熟悉构成几何圖形的基本元素，让学生能够熟练地将直观图分解为基本的几何元素，并且能动手画出一些常见的几何图形。例如，在认识长方形的过程中，先引导学生观察生活中常见的长方形物体，如课本、课桌、门窗等，并用直尺、量角器等测量工具测量图形，初步认识长方形的基本特征（4个角都是直角，对边相等）;再引导学生观察不同的长方形以及与长方形相似的几何图形（平行四边形、梯形），让学生进行对比、识别，从而掌握长方形的基本特征。

二、图形转化，提升析图能力

小学高段学生逐渐从具体形象思维转向抽象逻辑思维，但仍以具体形象思维为主去认识事物。在提升学生几何识图能力之初，教师可以将直观图进行分解，抽出一部分让学生先认识图形各方面的特征，再从整体上对图形进行认识。从部分到整体的教学也是融人图形转化的策略，如平行四边形、三角形以及梯形的面积公式都是通过将原图形切割、移补或组合，转化为长方形、平行四边形来推导的;圆柱的体积公式是通过转化为长方体来推导的。

1.“静”转化为“动”，分析关系

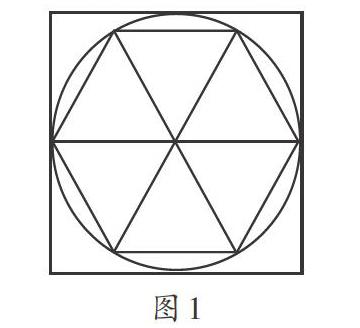
图形变换其实可以看作图形运动。例如，教学“圆的周长”时，笔者通过图形转换，让学生感受到圆的周长可能与直径存在一定关系。笔者还让学生根据之前学习的知识思考：“正方形的周长是边长的4倍，长方形的周长是其长宽之和的2倍，那么圆的周长和直径会不会存在一定的倍数关系？如果存在，会是几倍呢？”笔者让学生观察图l，并在正方形里画出一个最大的圆，再在圆内画出一个最大的正六边形，最后提出自己的猜想。

问题1：哪个图形的周长最长，哪个图形的周长最短？

问题2：正方形、正六边形的周长分别是圆的直径的多少倍？

问题3：圆的周长大约是其直径的多少倍？

前两个问题学生只需观察与分析就可以得出正确答案：圆的周长比正方形的短，比正六边形的长;正方形的周长是圆的直径的4倍，正六边形的周长是圆的直径的3倍。由此可以分析出问题3的答案：圆的周长与直径的倍数关系应该在3-4之间，所以圆的周长，直径=3.（？）。通过多种几何图形的特征对比实现图形间的转化，古代圆周长计算正是这样探索出来的。启发式的设问让学生将脑海中静态的几何图形转为动态，从而理解圆周长与其直径的关系，为学生进一步掌握圆周长计算公式打下了基础。

2.画图分割转化，分析信息

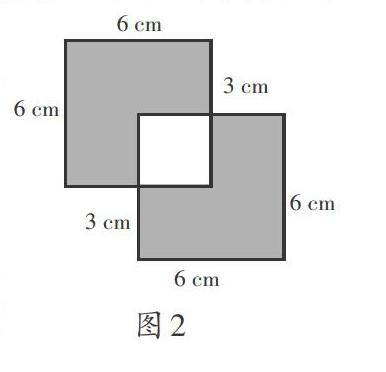
数学学习中，仅凭显性数学信息往往很难解决问题，有很多必要的数学信息是内隐的，需要学生充分利用经验和所学知识去多角度解读。放在“图形与几何”中，则需要学生通过分割和转化，分析有关信息。例如：如图2所示，你能算出阴影部分的面积吗？

图中繁多的数据让学生头昏眼花，有些学生还没有分析题目就已经放弃了。教师可以对已有图式做出改进，帮助学生将题目中的信息进行恰当的演变，如启发学生进行想象，或是对图形进行相应的移补，又或是画上几条辅助线将图形进行分割，就能把复杂的数学问题剖析透彻，降低问题的难度，从而轻松整理出解题思路。

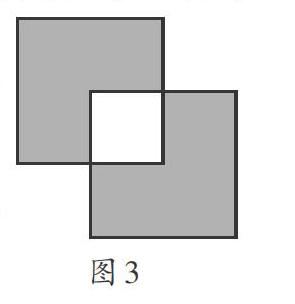
方法1：想象

把两个一模一样的正方形如图3所示叠在一起，空白部分是两个相同的小正方形，阴影部分的面积就等于两个大正方形的面积减去两个小正方形的面积。因此，解题所需要的信息只是大正方形的边长和小正方形的边长。

方法2：移补

把其中一个正方形向上或向下平j方形（如图4）。学生一眼就能够看出长方形的长是9厘米，宽是6厘米，此时利用长方形面积公式就能计算出阴影部分的面积。

方法3：分割在图中添加适当的辅助线，把阴影部分分割成6个完全相同的小正方形，阴影部分的面积就是这6个小正方形面积之和。因此，解题时只需要知道小正方形的边长。

从以上案例可以发现，将图形进行适当的运动，如想象、移补、分割等，把不规则图形变成规则图形，有利于降低问题的难度，从而整理出解题思路。“图形与几何”的有关问题中经常会出现一些多余的数学信息，对学生思维产生干扰。当学生能正确判断哪些数学信息是多余的，哪些是需要转化的时候，就说明学生真正地领悟了数学信息之间的联系。而明辨数学信息既是学生对数学知识掌握的过程，也是学生个体智慧的训练过程。

三、数形结合，提升辨图能力

“数”与“形”两者之间是相对应关系，数形结合就是把抽象、复杂、难懂的数学符号、语言、关系与直观形象的几何图形结合起来。换句话说，数形结合就是把复杂抽象思维与直观形象思维相结合。这样做可以把复杂的问题变简单，把抽象的问题变得具体形象。数形结合数学思想方法在小学数学教学中有着十分广泛的应用，在几何图形教学中更为突出，对比辨析地运用这种教学思想，可以获得事半功倍的效果。

1.巧用图形组题，让学生明辨其规律

例如：图6中，摆1个正方形用了4根小棒，摆2个正方形用了7根小棒，像这样摆下去，摆5个正方形用（）根小棒，摆n个正方形用（）根小棒。

笔者让学生接着画一画摆3个正方形、4个正方形，观察各需要几根小棒。学生发现，每增加1个正方形就多用3根小棒，由此很快得到第一个结论：每增加1个正方形就多用3根小棒，因此摆5个正方形需要16根小棒。笔者再引导学生观察数据，学生发现从4→7→10→13→16，这组数据的变化规律可以用算式表示：3x1+1→3x2+1→3x3+1→3x4+1→3x5+1。筆者问：“每个算式里都有一个‘+1，这个‘1代表什么呢？”学生回答：“可以代表最左边的1根小棒，也可以代表最右边的1根小棒。”笔者接着提问：“摆8个正方形需要几根小棒？用算式怎么表达？摆21个呢？摆99个呢？摆n个呢？”学生回答：“8x3+1 =25，2lx3+1=64，99x3+1=298. 3n+l。”笔者通过追问，把学生的思维从具体的算式发展概括成一般规律。

在此基础上，笔者把正方形变成正六边形（如图7），问：“摆1个正六边形要6根小棒，摆2个正六边形要11根小棒，摆3个呢？摆8个呢？摆n个呢？”学生分析每增加1个正六边形，就要多用5根小棒，所以摆3个要3x5+1=16（根），摆8个要8x5+1=41（根），摆n个正六边形所需的小棒根数就可以用5n+l来表示。式子里“1”也表示图形中最左边或最右边的1根小棒。

笔者继续提问：“1006根小棒可以摆多少个正六边形？”学生思路清晰地回答：“先减掉最左边或最右边的1根，再除以5，列式为（1006-1）÷5=201（个）。”

在学生掌握该类型题的解题思路后，笔者出示练习题：如图8所示，某小学使用的是正六边形实验桌，每张实验桌可以坐12人（每边坐2人），将实验桌拼起来，2张实验桌能坐20人，按这样的拼法，5张实验桌拼成一排后可以坐（）人，x张实验桌拼成一排可以坐（）人。

学生观察发现每增加1张桌子就多了8人，其中上面和下面各多了4人，而左右两边的人数是不变的，所以5张实验桌这样拼在一起后一共可以坐5x8+4=44（人），x张实验桌就可以坐（8x+4）人。笔者问：“8x+4中的‘4表示什么？”又指着算式3n+1问：“求小棒根数与求人数这两个算式区别在哪里？”再一次让学生明晰两种算法的异同点：不同点在于求小棒根数要加左边或右边的根数，求人数要加左右两边的人数;相同点在于每次增加的根数（人数）都与正方形个数（实验桌张数）成倍数关系。

2.画出图式，让学生明辨其概念

小学生的数学思维正处于成长阶段，他们对很多数学概念都比较模糊，特别是对面积与周长。这部分知识本身就较为抽象，理解难度大。把这两个概念放一起形成数学问题，问题难度就会提高好几个层次。这时，图式就体现出了它的价值，我们可以利用直观的图式来表达题目中抽象、概念性的东西。

例如：周长相等的一个正方形和一个长方形，它们的面积（）。

A.相等 B.不相等C.可能相等，也可能不相等

解决问题时不妨假设长方形和正方形的周长都是12cm，在方格图（每个小正方形的面积是lcm2）中画出几个图形（如图9）。显然，周长相等的正方形和长方形，面积并不相等。

通过画图，将枯燥的文字和形象的图式有机结合，使抽象问题变得形象直观、简洁明了，同时也能帮助分析题意、明辨概念，将模糊的概念清晰化。

“图式”在解释问题现象时带来的视觉冲击使我们对知识的理解超出了通窍的范围。教师教学时运用数形结合思想与辨析对比方法，将复杂难懂的数学问题转化成简单的问题，促使学生对知识的认识、理解逐步深化。

四、交流合作，打破识图定式

传统小学数学几何教学为教师示范、学生操作的感知形式，但没有哪种途径比学生自己去探索、去发现新知更为高效，通过各类存在可能性的实验得出的结论最能够提升学生的几何识图能力。因此，教师应打破传统的教学思维模式，为学生设计合理的探究活动，指导学生展开探究式学习，以小组学习的形式探索新知。

例如，在教学“圆柱的认识”时，笔者提问：“刚才我们用这张长方形纸通过旋转得到圆柱，还可以用什么方法得到圆柱呢？”笔者让学生先思考再动手操作。学生动手操作后明确，还可以通过卷长方形纸得到圆柱。笔者趁机抛出一个具有挑战性的问题：“卷成的圆柱的侧面积跟长方形有什么关系？”有效地激发学生进一步思考。在小组讨论中，学生各抒己见，有的说圆柱侧面展开就是长方形;有的补充说圆柱侧面的面积与长方形的面积是相等的;有的说如果竖着卷，长方形的宽就是圆柱的底面周长，长方形的长就是圆柱的高;还有的说如果横着卷，那么长方形的长就是圆柱的底面周长，长方形的宽就是圆柱的高。在小组讨论和演示中，学生全面认识了长方形和圆柱侧面之间的关系，学会了把陌生的曲面转化成熟悉的平面图形。通过小组合作积极探究问题的本质，教学过程变成一个动态的学习整体。

综上所述，不难发现当前很多高段学生并不重视锻炼自身的几何识图能力，教师也不太关注和培育学生的几何识图能力，致使学生对“图形与几何”的课程内容不够熟悉，空间观念和几何直观能力都不理想，严重影响其数学核心素养的提升。因此，教师一定要明确空间观念与几何识图能力培养的重要价值，努力激发学生学习空间与几何图形的兴趣，有针对性地培养小学高段学生的几何识图能力，全面提升学生的数学核心素养。

[参考文献]

[1]邹霞.信息技术在小学数学“图形与几何”课堂教学中的应用[J].数学大世界（上旬）.2016（07）：36-37.

[2]王淑华.小学数学中几何图形概念的教学策略[J].中华少年.2015（ 27）：135-136.

[3]刘晓岚.刍议小学数学中几何图形的教学方式[J].新课程（小学）.2015（ 06）：146.

[4] 刘淼.小学数学教学中的“数形结合”探究[J].中国校外教育.2015 （14）：143.

[5] 梁娴雅，几何直观在教学中的有效运用[J].时代教育.2015（ 08）：275.

（责编吴美玲）