基于APOS理论下的小学数学概念教学的研究

刘祥

[摘要]美国著名数学教育家杜宾斯基提出的APOS理论把数学概念教学分为四个阶段：活动阶段、过程阶段、对象阶段、图式阶段。以小学数学中的“分数的初步认识”教学内容为例，以APOS理论为基础，借助多媒体软件设计概念教学的四个阶段。通过创设真实的活动情境，使学生感悟分数;开展小组合作探究，使学生理解“分数”的概念;建构对象实体，促学生把握“分数”的本质;建立深层图式，助学生形成概念的基本体系。

[关键词]APOS理论;概念教学;分数

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）11-0022-03

一、问题提出

美国的数学家杜宾斯基提出的APOS的理论认为，作为学习者不能直接学习到数学的概念，而是要通过一些心智结构使得所学的概念产生实际的意义，教学的真正目的是要帮助学习者建立合适的心智结构。APOS理论以活动、过程、对象与图式四个具体的阶段体现了数学概念的形成与思维过程。

执教教师以APOS理论为指导，借助多媒体演示动态生成的全过程来设计概念教学过程的四个阶段，有助于学生学习“分数的初步认识”中的概念。

二、APOS理论的概念教学阶段与多媒体的运用

杜宾斯基认为，任何一个数学教育中的理论或模型都应该致力于对“学生是如何学习数学的”以及“什么样的教学计划可以帮助这种学习”的理解，而不仅仅是陈述一些事实。正是基于这样的考虑，杜宾斯基建立了APOS理论，而APOS理论中包含四个基本的阶段：

1.活动（Action）阶段

“活动阶段”是指个体或学习者通过一步一步的外显性（或记忆性）指令去变换一个客观的数学对象，它是学习者获得数学概念不可缺失的条件。在小学数学中，许多的概念都是“隐性”的，需要通过一些外显的探究活动去获得概念的本质。在数学概念的教学中，借助多媒体教学，能够将教学的对象动态地呈现在学生面前，通过有效操作，产生良好的教学效果，从而让学生感悟“分数”的本质，由此能够获得概念的表象。

2.过程（Process）阶段

“过程阶段”是外显数学的活动思考的过程，当“活动”经过多次的重复而被个体熟悉后，就可以内化为一种称之为“过程”的心理操作。有了这种“过程”，个体就可以想象这个“活动”，而不需要通过外部的刺激;他可以在头脑中实施这个过程，而不需要具体操作;进而，他还可以对这个过程进行逆转以及与其他程序进行组合。学生多次重复和熟悉之后，就能进行一系列的心理活动，抽象出数学概念的本质属性。在数学概念的获得中，可以借助多媒体将数学的对象转化为动态图像，通过演示帮助学生从图形中发现“分数”的本质。

3.对象（Object）阶段

当个体或学习者能够把“过程”作为一个整体进行操作时，这一过程就变成了一种心理“对象”。借助多媒体将概念的对象做一系列的动态操作演示，就能帮助学生把握概念的特点及性质，深层次认识概念。

4.图式（Scheme）阶段

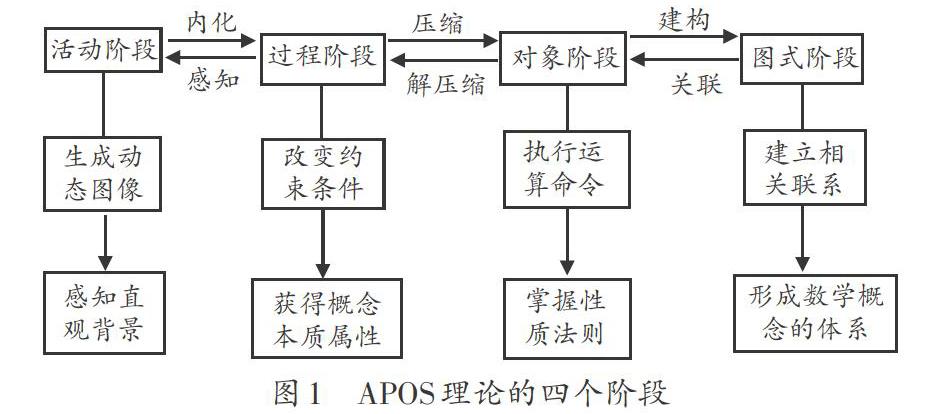
一个数学概念的“图式”是指由相应的“活动”、“过程”、“对象”以及与某些一般原理相联系的其他“图式”所形成的一种个体头脑中的认知框架，它可以用于解决与这个概念相关的问题。从这个意义上看，APOS理论中的“图式”有点类似于韬尔的“概念意向”。以上四个阶段及其关系如图1所示：

按照杜宾斯基的解释，上述四个成分中，“活动”、“过程”和“对象”也可以看作是数学知识的三种状态，而“图式”则是由这三种知识结构构成的一种认知结构。此外，上述四种结构成分的排列虽然在理论上具有一种等级结构，也就是说，一般情况下前一成分的建构是后一成分的基础。APOS理论认为，在数学学习中，在恰当引导前三个阶段后，学习者本身在建构与反思的基础上能够形成图式，进而厘清问题的情境，获得数学概念的本质。本文以俞正强老师教学的“分数的初步认识”为例，以APOS理论为指导，借助多媒体探索小学数学概念教学的过程。

三、分数的初步认识概念教学设计

1.创设真实的活动情境，初步认识“分数”

依据《义务教育数学课程标准（2011年版）》，学生在学习分数之前，对分数并不了解，也不知道怎么读与写，所以在引入分数的概念之前，俞老师并没有直接给出分数的概念，而是通过创设具体的情境，使得学生逐渐体会整数与分数，慢慢抽象出分数的概念。

師：大家吃过月饼吗？

生（齐）：吃过。

师：请看大屏幕。今天老师带来一些月饼，这是几个月饼呢？

生1：一个。

师：老师又带来这样的月饼，你们猜猜看是多少呢？

生2：半个。

生3：半个。

师：你们太聪明了。

根据APOS理论，在最初的活动阶段，学习者通过一步一步的外显性（或记忆性）指令去变换一个客观的数学对象，它是学习者获得数学概念不可缺失的条件。通过有趣的对话活动，教师慢慢唤醒学生对分数的认知，了解学生已有的知识与经验。通过创设一个月饼到半个月饼的情境，引发学生学习数学的兴趣，并逐渐抽象出数字“1”和“半个”（该怎么表示呢？），激起学生学习分数的热情，为进入APOS的下一个阶段做好准备。

2.开展小组合作探究，理解“分数”的概念

师：“半个”月饼用哪个数字来表示呢？请开展小组合作探究。

师：在学习“半个”月饼用哪个数字表示之前，思考一下，这半个月饼是从哪里得来的？

（大屏幕演示“一个月饼”到“半个”月饼的动画）

生1：半个月饼是从一个月饼里得来的。

生2：半个月饼是把一个月饼分成了“两半”。

生3：把一个月饼“平均”分成了“两半”，那么半个月饼就出现了。

师：是的。把一个月饼平均分成了两块，取出其中的一块。平均分成两块，在数学里我们用数字“2”表示;取出其中的一块，我们用数字“1”表示;平均分，用一短横进行表示。因此我们用“1/2来表示这个“半个”。

师：这个数怎么读呢？

生4：二分之一。

根据APOS理论，在这一阶段，学习者需要对数学活动做进一步的思考。教师借助多媒体动画演示，通过操作由“一个月饼”到“半个”月饼的形成过程，让学生通过观察、比较、分析、归纳等一系列的探究过程，概括出数的特点。在整个APOS的第二个过程中，让学生对这样的“数”有了初步的感觉。

3.建构对象实体，把握“分数”的本质

在多媒体技术的支撑下，俞老师列举多个分数的实例，使学生可以从不同的角度去逐渐体会并建构“分数”的概念，经历由一个月饼到半个月饼再到1/3个月饼，最后到1/4个月饼，由特殊的“1”到一般的分数的建构过程，很好地抽象出分数概念的本质特征：分数就是把“一个”单位“1”平均分成若干份，其中的每一份可以用分数表示。俞老师帮助学生建构“分数”的概念之后，又帮助学生了解了“分数”具体的量和“分量”的区别。

师：半个月饼可以用哪个数字来表示？

生1.1/2

师：“1/2”和“1/2个”有什么区别和联系呢？

生2：单独的1/2表示的是“把一个整体平均分成两份，其中的一份就用1/2表示。

生3：“1/2个”表示一个物体的一半，是具体的数

量。例如妈妈给我一个苹果，我吃了这个苹果的半个，也就是1/2个。

根据APOS理论，教学该阶段的目的是要帮助学生抽象出分数概念的本质特征，实现对分数概念的更深层次的认识和理解。在多媒体辅助教学的环境下，俞老师利用多媒体展现从多个动态的实例中抽象出分数的本质概念，让学生更直观地看到分数的产生与变化的全部过程。分数的概念具有运算的规则“实体”，即对象。学生学习了分数的概念之后，从“过程”阶段进入了“对象”阶段，这里，“对象”阶段发挥了多媒体的优势，突出了分数教学的重点，提升了课堂的教学效率，吸引了学生学习分数的热情与兴趣。

4.建立深层图式，形成概念的基本体系

根据APOS理论，图式阶段是建立概念联系的阶段，即学习者能够建立新的知识结构，形成新的概念体系。多媒体可以直接呈现分数的产生与变化的过程，能够引导学生对分数的认识更深入。

师：吃了半个月饼后，还剩几个月饼？

生1：还剩半个，因为是把一个月饼平均分成了两半，吃了一半，所以还剩一半。

师：如果把一个月饼平均分成三块，吃了其中的一块，还剩多少？

生2：还剩三分之二个，因为是把一个月饼平均分成三份，只吃掉了其中的一份，还剩下两份，所以剩下的部分占整体的三分之二，即可以用三分之二表示。

人教版教材三年级下册创设了两位学生分月饼的情境，由“简单的一个月饼怎样才能够分给两个学生吃呢？”引发学生思考后得出半个可以用分数表示，符合学生的认知规律，学生比较容易得出分数的概念。

从以上教学可以看出，多媒体能够帮助学生发现知识的内在联系，建立深层次的图式，逐渐建立分数的概念体系。在数学课堂教学中，APOS的四个阶段是紧密相连、环环相扣的，在相互作用的条件下完成了对分数概念的建构，让学生对分数的概念理解得更深刻。

四、思考

本节课是“分数的初步认识”第一节课，分数对于学生来说是比较陌生的，在课堂中帮助学生建构分数的概念就十分关键。俞老师的这节课恰恰是基于学生已有的生活经验，让学生逐步理解分数的概念。首先，创设真实的活动情境，让学生初步认识分数;接着，让学生合作探究，说一说自己对分數的看法;紧接着，让学生建构对象的实体，理解分数的本质;最后，让学生建立深层图示形成分数的概念体系。整堂课设计非常巧妙（感知分数——建构分数的概念——理解分数的概念），贴近学生的实际生活，抓住学生的心理特征，让学生在愉快的氛围中去学习并掌握分数的概念，这正体现了“教师是学生的组织者、引导者与合作者，学生是学习的主体”，把课堂还给学生，让学生用数学的思维去思考现实的世界，用数学的语言表达现实的世界，用数学的眼光观察现实的世界。

从数学学习心理学角度看，APOS的理论是合理的，反映了学生学习数学概念过程中真实的思维活动。据了解，该理论主要应用于大学数学教学的研究，但也同样适用于小学数学的概念教学，特别是与多媒体信息技术相结合的情况下，能够很好地突破学生的认知水平，令课堂教学取得意想不到的效果。

[参考文献]

[1]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

[2]乔连全.APOS：-种建构主义的数学学习理论[J].全球教育展望，2001（3）：16-18.

（责编金铃）