基于BP神经网络预测变壁厚薄壁深孔件挤压力∗

2020-05-15吴志林程宇梁陈智仁

计算机与数字工程 2020年2期

张能吴志林蔡松程宇梁陈智仁

（1.南京理工大学机械工程学院南京 210094）（2.常州哈步机电科技有限公司常州 213000）

1 引言

变壁厚薄壁深孔件由于变形抗力和摩擦力大导致挤压力会很大，而过大的挤压力会导致模具损坏，从而不能制备出尺寸合格的样品。在进行变壁厚薄壁深孔件的制备前，需要对挤压力进行计算，然后根据模具的强度估算出能制备出的最薄壁厚或者最深深度的盲孔件。传统挤压力的计算公式主要有主应力法、功平衡法、极值原理包括上限定理和下限定理和滑移线法［1～4］。郭胜利［5］等用主应力法计算的挤压力平均误差约为11.56%。张浩然［6］等通过上限法计算挤压力，当挤压比小于4时，理论计算与有限元模拟结果误差小于10%；当挤压比大于5时，两者误差小于20%。可以发现，通过理论公式计算出来的挤压力误差都比较大，且计算过程复杂。

基于BP神经网络，本文以样品的壁厚和挤压力的关系为研究对象，建立了一个1输入1输出，单隐藏层的简单BP神经网络模型，对7050铝合金变壁厚薄壁深孔件的热挤压力进行了预测，为样品尺寸的确定和挤压机的选择提供了参考依据。文中的BP神经网络程序的实现是基于python编写的。

2 基于有限元模拟软件的挤压力计算

图1为变壁厚薄壁深孔件样本的剖面图，与常见的盲孔管材相比，其壁厚不是均匀的，内壁是由一段圆弧和一段有较小倾斜角的斜线构成的。对样本尺寸的要求为底厚和样品高度为定值，且内壁尺寸形状也固定，故用于挤压的磨具模芯尺寸也是一定的，所以在一定挤压温度下模芯能承受的挤压力也是一定的。经试验研究发现，当薄壁深孔件的壁厚很薄时，由于挤压过程中挤压力过大会导致模芯墩粗，不能制备出尺寸合适的样品；同时随着样品壁厚的增加，挤压力会逐渐降低。所以需要计算出不同壁厚下挤压力的大小，从而根据模芯能承受的极限压力来推出反挤压能挤压出最薄壁厚的样品。

本文将采用有限元仿真软件DEFORM模拟计算反挤压的挤压力。由于样品是变壁厚的，样品的壁厚以样品口部最薄处的壁厚为准。初始条件为摩擦因子为0.4，挤压的温度为400℃，模芯的挤压速度为10mm/s，模芯的挤压步长为0.075mm/step。为提高仿真效率，采用Deform-2D对称模拟［7］。为保证计算精度网格类型采用四边形网格［8］，坯料网格划分点为4000个，同时坯料与模具间也存在传热，模具也需要划分网格，模芯网格划分点为2000个，模腔网格划分点为2000个，底座网格划分点为1000个。通过仿真获得了不同壁厚下挤压力大小的几组数据。

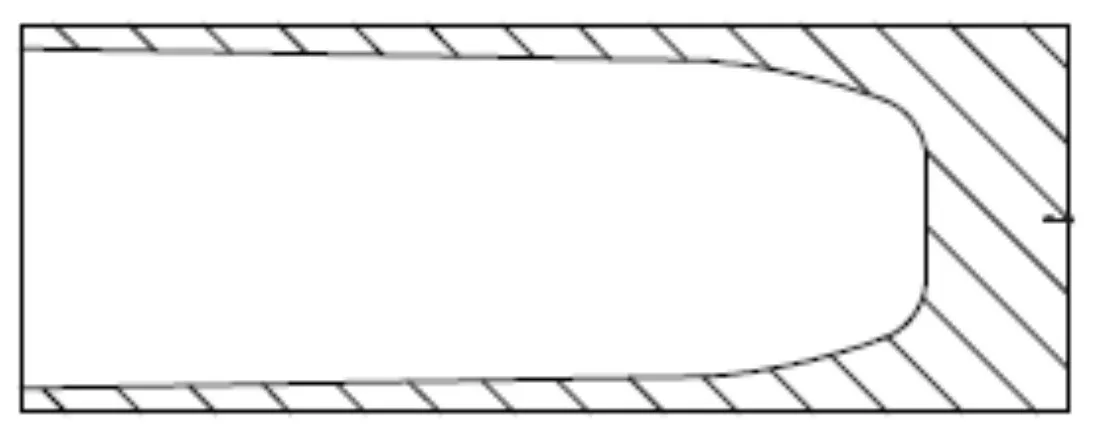
图1 样品剖面图

3 BP神经网络原理

BP网络可以学习并存储大量的输入-输出模式映射关系，而无需事先揭示描述这种映射关系的数学方程。由于在理论上已经证明具有三层结构的BP神经网络能够逼近任何有理函数［9］，本文将采用三层BP网络来建模以逼近反挤压中样品壁厚与挤压力间的函数关系，利用该函数关系来预测给定样品壁厚时的最大载荷大小，以此确定模芯能够承受的最大载荷下所能挤压出的样品最薄壁厚。从而对样品尺寸的设计提供参考，避免因前期试验而造成的经济损失，降低研发周期，节约成本［10］。

3.1 BP神经网络模型

BP神经网络模型如图2所示。

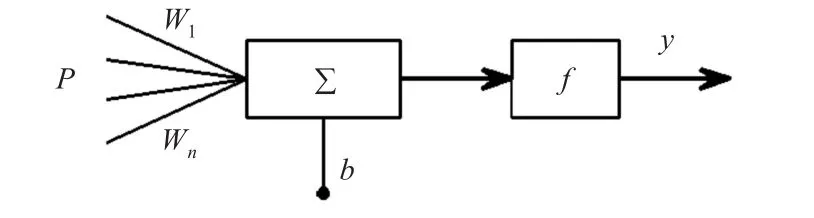
图2 BP神经网络模型

BP神经元的输入为P，权重和阈值分别为w和b，线性神经元模型的输出为y。BP神经元的传递函数为非线性函数，最常用的传递函数有Sigmoid、Tanh和ReLU函数，如图3所示。

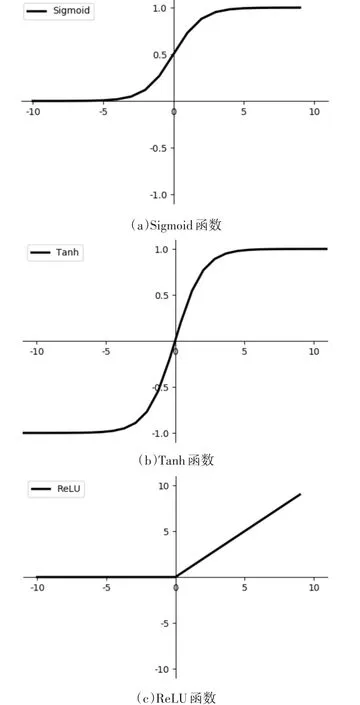
图3 BP神经网络常用的传递函数

Sigmoid函数和Tanh函数都有一个缺点，就是当输入非常小或非常大时导数的梯度或者说这个函数的斜率可能就很小，接近0，这样会拖慢梯度下降算法。而ReLU函数不存在上述问题，同时由于ReLU函数会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。本文中选取ReLU函数为传递函数。

BP网络是一个由输入层、隐藏层和输出层组成的多层前馈神经网络［11］。图4是一个典型的三层BP神经网络结构图，每层之间采用全互连方式，且同一层之间不存在互相连接，隐藏层可以有一层或者多层。

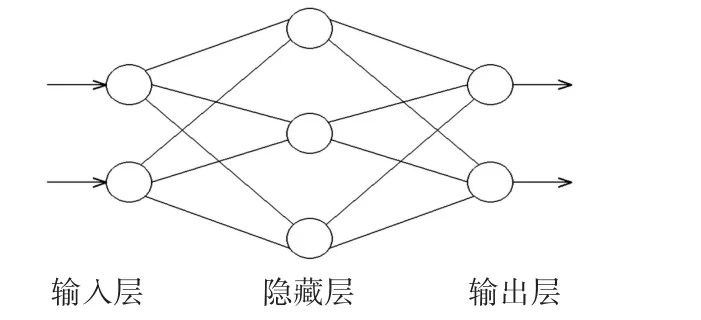
图4 典型三层BP神经网络结构图

BP网络的学习过程由向前计算过程和误差反向传播过程组成［12］。在向前传播过程中，输入值从输入层经隐藏层逐层计算，并传向输出层，每层神经元的状态只会影响到下一层神经元的状态。如果输出层不能得到期望的输出，则转入误差的反向传播过程，误差信号沿原来的连接通路返回，逐层调整网络各层的权值和阈值，直到到达输入层，再重复计算。

3.2 BP神经网络算法

基本的BP神经网络算法是由两部分组成：信号的向前传播和误差的反向传播［13］。即计算预测输出时按从输入到输出的方向进行，而权值和阈值的修正从输出到输入的方向进行。BP神经网络算法的公式如下。

3.2.1 信号的前向传播过程

隐藏层第i个节点的输入neti为

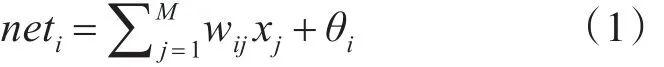
隐藏层第i个节点的输出oi为

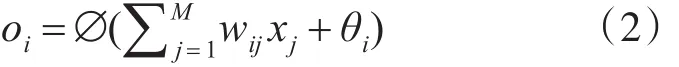
输出层第k个节点的输入netk为

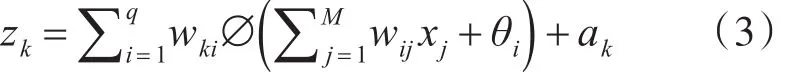
输出层第k个节点的输出ok为

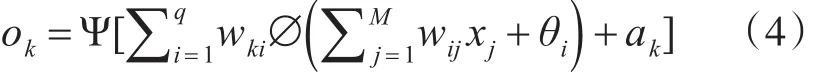
3.2.2 误差的反向传播过程

对于每一个样本p的二次型损失函数为

系统对P个训练样本的代价函数为

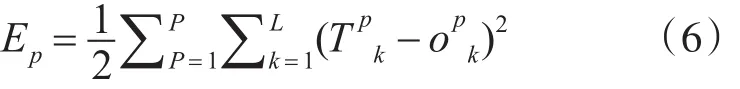
则有：

输出层权值调整公式为

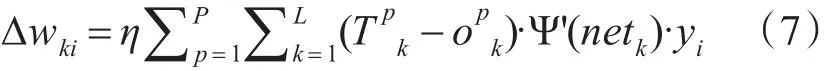
输出层阈值调整公式为

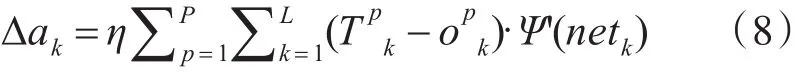
隐藏层权值调整公式为

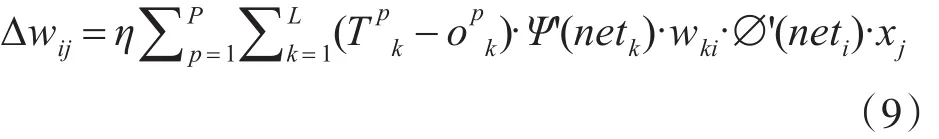
隐藏层阈值调整公式为

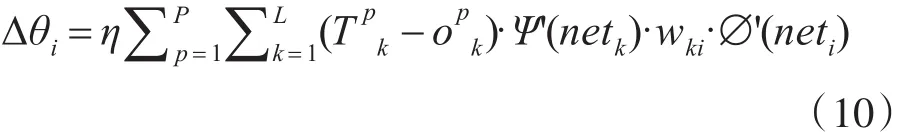
其中：wi，j是隐藏层第i个节点和输入层第j个节点之间的权值；θi为隐藏层第i个节点的阈值；∅为隐藏层的激励函数；wk，i是输出层第k个节点到隐藏层第i个节点之间的权值，i=1，…，q；ak表示输出层第k个节点的阈值，k=1，…，L；Ψ为输出层的激励函数，ok为输出层第k个节点的输出。

3.3 BP神经网络的创建

通过面向对象编程语言python，并结合上述向前和反向传播公式，创建BP神经网络预测的程序。其中：输入层节点数为1，代表样本壁厚；隐藏层节点数为4；输出层节点数为1，代表反挤压过程中最大载荷；隐藏层和输出层激活函数都选用Re⁃LU函数。

4 预测结果

将有限元模拟软件计算得到的几组不同壁厚下挤压力大小的数据训练上述建立的神经网络模型，设定学习率为0.15，迭代次数为500，目标误差为10-3。然后对设置好的BP神经网络进行训练，训练收敛后即可对给定的壁厚进行挤压力的预测。图5为误差-迭代次数曲线图，经过74次训练，BP神经网络收敛。表1为数值模拟与BP神经网络预测值的对比。由表知，实际输出值与期望输出值的相对误差较小，这说明经过训练建立的神经网络模型可以快速预测最大挤压载荷。

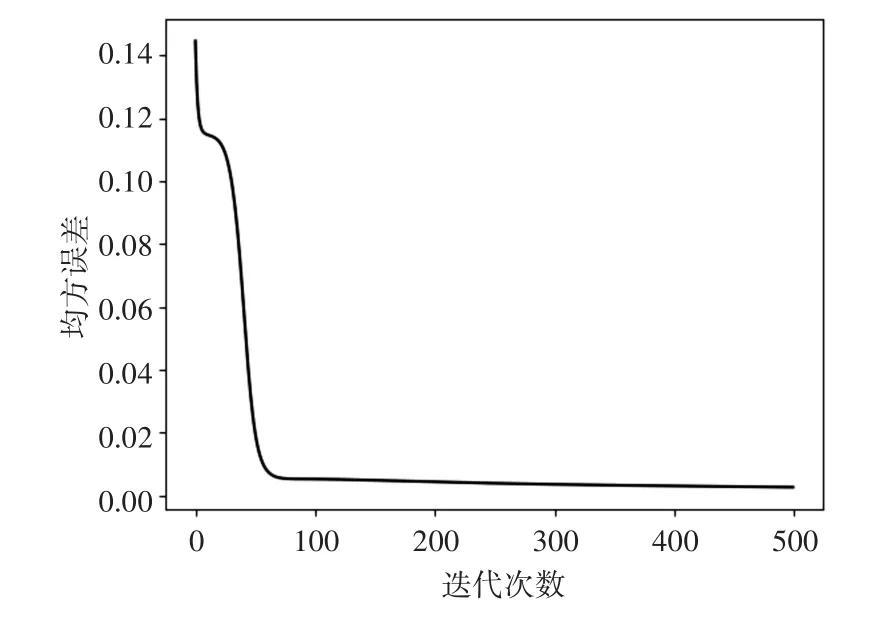
图5 误差-迭代次数曲线

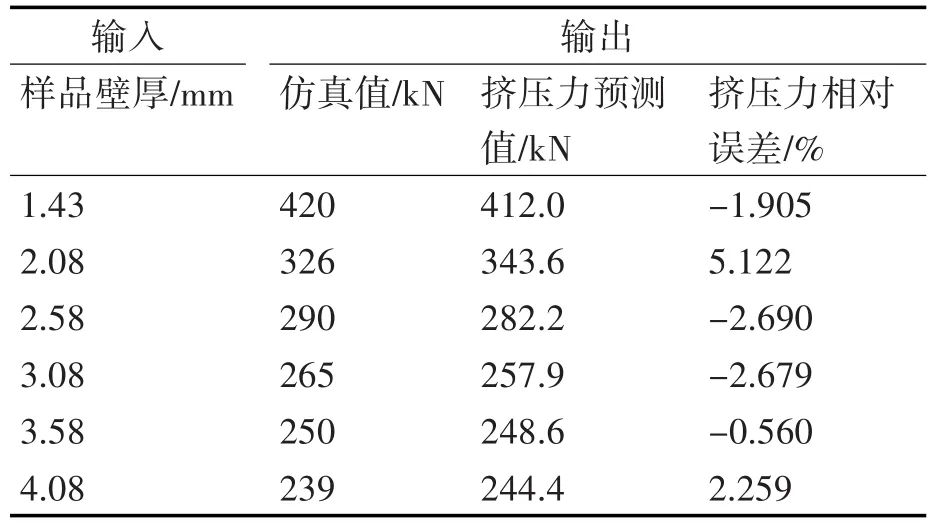
表1 仿真值、预测值和相对误差

5 算例

在7050铝合金热挤压中，模芯采用的是H13热作模具钢［14］。H13钢在600℃以下使用时，其屈服强度达到950MPa［15］。根据样品的设计尺寸可推出模芯的直径大约为19.5mm，即可得出模芯在挤压过程中不发生塑性变形时能承受的最大挤压力再根据BP神经网络对不同壁厚下的挤压力大小的预测模型，可预测出：在样品内径和挤压深度一定的情况下，采用反挤压加工7050铝合金变壁厚深孔件所能得到的最薄壁厚约为2.56mm。