基于改进增强型神经网络的短期电力负荷预测∗

袁小凯 李 果 许爱东 张乾坤 张福铮

（南方电网科学研究院 广州 510080）

1 引言

考虑到历史电力负荷数据、天气、时间等信息影响，电力负荷预测用于预测未来的电力负荷，对于独立的系统操作而言，有许多电力负荷预测应用向调度员提供信息和市场操作，比如发电调度、系统储备生成，因此准确的电力负荷预测模型是规划管理和运行的必要条件［1～3］。电力负荷预测在帮助电力企业购买和发电、负荷开关、电压控制、基础设施建设等方面做出重要决策具有重要作用，同时对能源供应商、金融机构和其他参与发电、输电、配电和市场营销的参与者也非常重要。通常根据预测的持续时间，将负荷预测分为长期预测和短期预测。长期负荷预测的时间跨度为几个月至数年，而对未来一周进行的预测通常称为短期负荷预测。随着预测精度的提高，运行成本的降低和电力系统运行的可靠性也随着提高。本文主要研究短期电力负荷预测，因为它与电力系统的经济和安全运行密切相关。由于电力系统运行的经济性和可靠性受电力负荷的影响较大，成本节约主要依赖于负荷预测的准确性。主要调度中心的负荷调度员负责通过购买、销售和调度电力来维持和控制电力的流动。调度员需要预先对负荷模式进行预估，以便分配足够的发电量来满足客户的需求。过高估计未来的负荷可能导致不必要的发电机组启动，从而导致储备和运营成本的增加。低估未来负荷将导致为系统提供操作储备和稳定性的失败，这将导致电力系统网络的崩溃。

负荷预测的方法主要包括传统和人工智能两种，前者包括时间序列、多变量回归和状态估计方法，后者包括模糊逻辑［4］、支持向量机［5～6］、人工神经网络（ANN）［7～8］和预处理训练数据的方法，然后利用预处理后的数据使用多个ANN进行负荷预测。传统的方法具有简单性的优点，而人工智能的方法具有较高的预测精度，因为它们可以精确地模拟所观测到的负载与所观测到的负载与所依赖变量间的高度非线性关系。

在本文中，通过集成学习算法提高了预测精度。在集成学习算法中，结合一组预测模型来提高预测精度。理论和实验研究表明，当群体中的ANN是准确的，并且每个网络的误差与该组的其他误差呈负相关时，可以通过投票或平均ANN的输出得到一个改进的精确泛化。在集成学习中，常用的两种算法是套袋法和增强法［9］。这两种算法都将单个预测模型的输出集合起来，以提高总体预测的准确性。已有成果表明，套袋法和增强法技术均比使用单个预测模型更准确。与使用单一的ANN相比，应用套袋法的ANN可以通过减少负荷预测误差的方差来提高负荷预测［10］。由于许多研究成果表明它可以产生较低的分类错误率，并且对过度拟合具有鲁棒性。本文提出了一种改进的短期电力负荷预测技术，基于迭代生成大量的ANN模型的增强型ANN（BooNN）算法，在每次迭代中，结果模型减少了预期输出之间的误差，并且在之前的迭代中得到了经过训练的模型所获得的误差［11］。同时使用一个前向阶段的加法模型，通过在前一次迭代中减去目标输出的加权估计值来更新每次迭代的目标输出。实验结果表明，该技术可以减少预测误差和预测精度的变化，与使用单一的ANN、套袋法ANN和其他技术相比，采用BooNN方法可减少计算时间，提高收敛速度。

2 人工神经网络

由于电力负荷负载的情况依赖于多种因素，如天气、时间、经济、电价、随机扰动和地理条件，所以提出了许多负荷预测技术，并应用于准确预测负荷模式。负载的情况多受到几个因素的影响，同时负载模式与影响因素之间的关系是非线性的。基于人工智能的算法在处理非线性关系时具有很大的优势，如模糊逻辑、支持向量机和神经网络，进行了大量的基于人工智能算法的应用负荷预测问题研究，因为可以执行比传统的短期负荷预测方法，如支持向量机和ANN，包括类似的小波神经网络和混合ANN模型等。在这些算法中，由于其易于实现和良好的性能，ANN模型已经广泛应用。

ANN是一个由人工神经元组成的学习系统，其试图模拟人脑的功能。通常ANN体系结构包括输入层、隐含层和输出层三层。第一层的输入由不同的因素或特征组成，对想要的预测输出有显著影响。隐含层利用这些特性来计算中间值，最后一层的输出由预测值组成。

ANN的每个隐含层都由N个神经元组成。每一层的输入乘以权重Wl，然后添加到偏差bl中。权重矩阵将输出从(l -1)层扩展到第lth层。例如在t时刻的具有F个特征的输入如下：

式中，W1是一个权重矩阵，b1是一个偏置向量，ρ1是一个激活函数。同时每一层的输出都是下一层的输入，因此，最终的输出有效地包含了每一层的权重输入和增加的偏差。最后一层L的最终输出是：

3 基于增强法的短期电力负荷预测

在短期电力负荷预测中，需要研究不同的独立参数对电力负荷的影响。通过给出在离散时间t=1，2，…，T内的 X过去值，可得到对应的观测值y，两者间可以用模型 f表示如下：

对应该模型函数 f̂需要符合如下条件：

1）估计值有较小的偏差，即前一次观测的负载y和负载 ŷ间的偏差应该较小。

2）预测值有较低的方差。在所有模型的平均预测中，不同模型的预测之间不应该有很大的差异。

3）该函数应避免过度拟合，即模型应该能够忽略观测中的随机误差。

模型通过已知的独立特征和依赖荷载观测得到，以及给出的预测的独立参数，可以用来预测下面的负荷。需要注意的是X和y可以看作是训练数据，因为通过它们可以建立描述两者之间关系的函数，并用该函数来预测未来时间对应的数据。

由于 f是一个高度非线性函数，类似ANN和SVM智能算法多用于快速逼近该函数。为了进一步提高负荷预测精度，本文采用了基于ANN的集成学习方法。使用一组ANN模型，通过对不同的数据集进行训练，得到每个ANN模型。将这组集合的模型融合在一起，得到最终的估计预测。

在分类问题上增强法得到了广泛应用，但还没有应用到许多回归问题［12～13］。利用 ANN提高负荷预测的目的是减少预测误差的偏差和方差，并且对过度拟合具有很强的鲁棒性。在推进过程中，通过模型迭代生成目标。首先，在迭代中，通过使用独立特性和依赖目标输出组成的原始训练数据，在第ith迭代时生成初始的模型ĥi。在下一个迭代次数i+1中，由第一个模型的预测错误代替输出目标生成第二个模型。

式中，hi是通过第i个模型得到的目标输出与实际输出之间的误差，αi是每个模型的权值。该过程一直持续到生成一定数量的M个模型，可以将所有这些模型形成一个集合F，该集合可以由一组估计 f̂的预测因子表示如下：

随后，将上述提出的预测器进行线性组合，可以描述如下：

式中，αi是第ith预测器的权值，该权值与每个函数的输出相乘并相加得到对应的最终输出。对于负荷预测问题，需要研究由独立变量Xtr和负载ytr组成的训练数据集。利用增强法的步骤如下：

1）首先，定义以下参数：模型迭代的总数为常数值M，在i=1，2，…，M 时，αi=α0，α0是0和1之间常数，

2）每个模型都是迭代生成。在第一次迭代i=1时，利用一下公式计算模型

3）从i=2到i=M ，残差 ∆y1

t更新如下：

利用更新后的残差计算一个新的ANN模型，如下：

在每次迭代中使用更新的估计值的权值，可避免只使用一部分参数带来的过度拟合。

4）在所有迭代的末尾，在每次迭代中将获得的所有ANN模型定义为集合。

5）结合给定的独立数据X，预测负荷以加权总求和的形式计算得到集合中所有模型的输出结果如下：

4 仿真结果

为了更好地比较提出算法的优越性，结合具体数据分别将BooNN算法与ANN、BNN、ARMA模型、HybANN和BRT算法进行比校［14～16］。

4.1 数据集

为了实现各算法比较的真实性，统一选取来自广州地区的历史小时温度和负荷模式，用作比较负荷预测的性能。用在训练和预测负载模式不同的独立参数包括干球温度、露点温度、一天的小时、一星期的天数、显示哪些天是假期或周末的标志、前一天的平均负荷，24h内负荷的差别，以及前一周相同天和小时的负载。作为短期负荷预测的这些参数，同样在负载模式上表现出相关的特点。对应的训练数据集包含由这些变量组成的数据向量，以及在这些数据所给出的时间内所测量的电力负荷对应的目标输出。将2014-2017年的样本用于训练，同时为了提高计算预测模型的准确性，将2018-2019年的样本也应用在短期负荷预测中。

4.2 在BooNN中选择ANN模型

通过不同的实验，得到了最佳性能的神经网络模型参数。第一个实验分别采用以下训练算法：Levenberg-Marquardt反向传播（LMB）、贝叶斯正则化反向传播（BRB）、弹性反向传播（RB）、梯度下降法和自适应学习速率反向传播（GDMAB）。隐含层和输出层的激活函数分别选为Sigmoid型和线性函数，因为这样的配置通过训练近似任何有限数目不连续的函数。输入层中神经元的数量选为8，该数目等于输入训练和测试数据中变量的数量。输出层中有一个神经元，因为最终的预测输出是一个标量。实验中只有一个隐含层，初始值从0到1不等。基于LMB和BRB的ANN表现出较好的性能，几乎与初始值无关，其次是RB和GDMAB算法。LMB用作接下来的ANN模型的训练算法。

表1 不同时间、节点数和隐含层时的MAPE值

下一个实验比较了ANN的性能，它具有不同的时间、节点数和隐含层数，如表1所示。在表中，N-LH表示在LH隐含层中神经元的数量。对于时间节点大于500，节点数大于20和隐含层数大于1的情形，在性能上没有显著提高。在200个时间节点内，MAPE会产生一个突变，其原因在于随着时间的减少，ANN可能没有经过适当的训练导致输出结果不稳定。在时间节点大于300或更大时，MAPE几乎保持不变。随着节点数目的增加，MAPE减少，而随着节点数量的增加，减少的百分比也减少了。此外，对于固定数目的节点，当层数大于2时，MAPE也增加。当节点数是20，隐含层从1到2增加时，MAPE的下降百分比非常低，同时20个节点、1隐含层的性能与10个节点、2个隐含层的性能相似。基于上述实验结果，在BooNN中使用的ANN模型，其选取参数为500个时间节点，一个隐含层中20个节点。

4.3 不同的样品迭代次数比较

不同迭代次数和训练样本大小对负荷预测精度的影响如表2所示。训练样本的大小从15000到35000，步长为500。迭代次数从5到25变化，步长为5。通过计算每个训练样本的大小/迭代次数得到的平均绝对百分比误差（MAPE）如下：

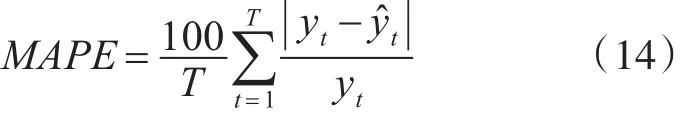
式中，yt是荷载的实际值，ŷt是荷载的预测值，t是荷载样本的总数量。可得到如下的结论：

1）对于每个迭代次数，随着训练样本数量的增加，MAPE减少。

2）从2000后开始的每个样本，25次迭代的MAPE比5次迭代的要小。

3）从迭代5次到迭代25次，MAPE渐渐减少，并在最小值附近波动。

4）当训练样本不足时，15000个样本的特性和迭代次数表现出不稳定。在这种情况下，随着迭代次数增加MAPE也增加，在一定数量的迭代后，容易导致过度拟合。

表2 不同采样数目和迭代次数时的MAPE值

图1进一步表明25000和35000个样本存在的特性。随着迭代次数增加，MAPE的波动会减少，特别是迭代次数大于20。35000个样本的MAPE比25000个样本的MAPE要小。虽然在最后这个差异更小，但是在每个迭代中新的训练模型有助于减少MAPE的值。

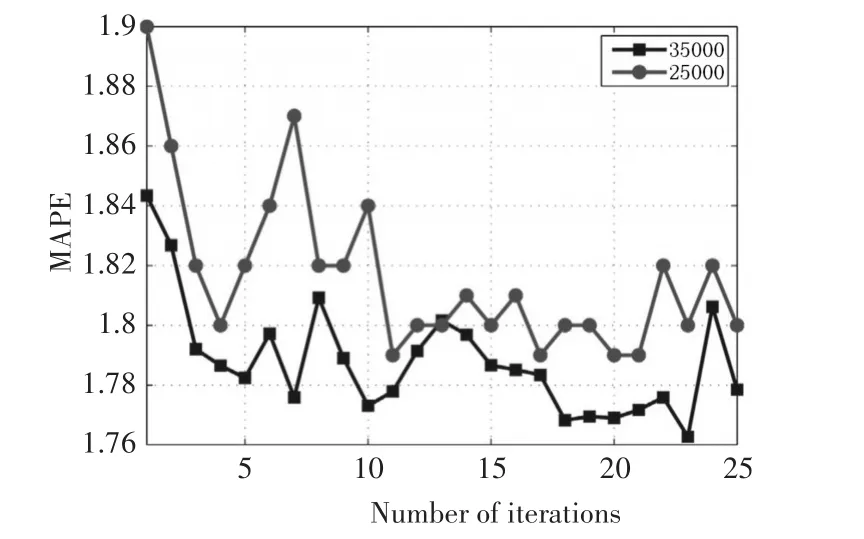
图1 迭代次数与MAPE值的关系

4.4 计算时间与权重对MAPE的影响

在改变权重时，MAPE的变化如图2所示。权重的变化从0.25到1.5，步长为0.25。为了便于比较，本文利用BNN进行了50次迭代得到MAPE，并给出了最佳的ANN。由于这两种方法的MAPE不受权重影响，对应为一个恒定的值。对样本数量为35000，迭代次数为25，可以看出在α＜1时BooNN的MAPE值小于ANN和BNN的值，这意味着权重α应该保持小于1。因此，在α＜1时BooNN与使用单一ANN和BNN相比提高了性能。

图2 权重与MAPE值的关系

在改变权重时，计算时间的变化如图3所示。权重的变化从0.25到1.5，步长为0.25。在权重从0.25到1时，BooNN的计算时间逐渐变小。从权重为1后，BooNN的计算时间逐渐增加。此外，从ANN和BNN的MAPE为常数值可以看出，虽然BooNN的计算时间大于单个ANN的计算时间，但比使用BNN少3到8倍。

图3 权重与计算时间的关系

4.5 单个ANN和套袋法ANN的比较

在权重α=0.5时，分别比较了ANN、BNN和BooNN算法的MAPE值，以及权重α=1时BooNN算法的MAPE值，如图4所示。可以知道：

1）BooNN的MAPE值与BNN的MAPE值近似或者小，相比于单个ANN的MAPE要小的多。

2）相比于BNN，BooNN的最大MAPE值较多，相比于ANN，则较少。虽然在权重α=0.5时，几乎没有样本的MAPE较大。

3）在权重 α=1时BooNN的MAPE值比权重α=0.5时分布的更广。在权重α=0.5时BooNN相比BNN拥有较低的平均值和相似变化，以及相对单个ANN有较低的变化，可以看出BooNN可以减小MAPE的变化。虽然对α=1而言变化更大，但是相比于ANN该分布已经大于一个更低的值。

图4 采用不同算法时MAPE的取值情况

4.6 与现有技术比较

将本文提出的算法与现有技术进行了进一步的比较，包括BNN，以及一种基于类似改进的小波神经网络（WNN）和BRT的自适应模型。为此，选择了2014年和2016年的广州训练和测试数据集。相比较上述算法，使用BooNN计算的月复月的MAPE和平均的MAPE均相对较小。图5显示了各种算法12个月的MAPE值。除了11月和12月，使用BooNN算法的每月MAPE值均小于SIWNN算法，尤其是在6、7和8这三个月。与BNN和BRT相比，除了7月份，比BNN稍高，BooNN算法的MAPE值总是最少的。使用BooNN算法得到的平均MAPE为1.43%，而BNN、SIWNN和BRT分别为1.5%、1.71%和2.44%。在提高预测精度方面，与现有其他技术相比，可以看出BooNN算法的优越性能。

图5 BooNN和SIWNN，BNN，BRT算法的MAPE值比较

图6 BooNN和ARMA，HybANN，BNN and BRT算法的MAPE值比较

下面，通过计算2018年的MAPE，将BooNN算法的性能与传统的ARMA、HybANN、BNN和BRT进行比较。从图6可以看出，相比上述算法，BooNN的MAPE均较小。虽然与BNN相比，两种算法的MAPE值相差不大，但是结合如图3可以知道，BooNN的计算时间比BNN少的多。因此，考虑到BNN的预测精度，BooNN在计算节省方面也有很大的提高。除ARMA外，其他技术与BooNN相比需要更少的时间，但是与BooNN相比，它们的性能要差很多。使用BooNN算法得到的平均MAPE为1.42%，而 ARMA、HybANN、BNN和 BRT分别为2.21%、1.94%、1.47%和1.93%，再次表明BooNN的预测精度较高。

5 结语

本文提出了一种改进的增强型神经网络（BooNN）的短期电力负荷预测算法，该算法包括一系列训练用的人工神经网络（ANN）。在每一次迭代中，利用训练的ANN模型，实现从前一次迭代的预测模型得到的估计值和实际值的之间误差最小。实验表明，当计算输出的模型数大于或等于20时，可以得到较低的预测误差。与单个ANN、套袋法ANN、改进的小波神经网络、ARMA、混合不受监督的ANN等算法相比，BooNN在降低误差方面表现较好，与BNN相比，节省了计算时间。使用直方图的统计分析进一步表明，使用BooNN得到的误差较低，与使用单一ANN和BNN相比，波动更小。