三步回归滤波建模的拓展及其在汇率预测中的应用研究

2020-05-15李小林司登奎

暨南学报(哲学社会科学版) 2020年5期

李小林，司登奎

一、引言

选取合适的方法并对关键经济变量进行准确预测不仅能够预防各种外生冲击带来的不利影响，还能有效调控经济运行进而维护经济平稳健康发展，因而具有非常重要的理论价值及现实意义。在现有的理论研究与实践应用中，最为常用的预测方法是选取与目标变量相关的预测因子，并采取相应的计量方法(如OLS)实现。然而需要指出的是，现实中可获得的经济变量的个数通常较多，甚至会接近或超过目标经济变量的样本总数，这就容易导致基于大样本理论的计量方法等性质极其不稳定甚至无法计算，从而导致预测精度降低甚至出现无效预测的情形。

如何从大量的可用经济变量中提取少量共同因子(Common Factors)是决定能否准确预测的重要前提。实践中，主成分回归方法(Principal Component Regression，PCR)是主流的提取因子并对目标经济变量预测的方法。(1)Stock,J. ,& Watson,M. ,“Forecasting Using Principal Components from a Large Number of Predictors”,Journal of the American Statistical Association,Vol. 97,2002,pp. 1167-1179.(2)Forni,M. ,& Reichlin,L. ,“Dynamic Common Factors in Large Cross-Sections”,Empirical Economics,Vol. 21,1996,pp. 27-42.(3)Bai,J. & Ng,S. ,“Forecasting Economic Time Series Using Targeted Predictors”,Econmetria,Vol. 146,2008,pp. 304-317.由于PCR方法的基本原理是从可用经济变量中提取因子，因此所提取的因子可以很好地解释可用经济变量的共同变化。但需要注意的是，提取出来的因子来源于可用经济变量，并不能确保所有的因子都和目标经济变量相关。因此，如果能够提取出和目标经济变量相关的因子无疑能够提高预测精度。

目前，学界在如何提取和目标经济变量相关的因子进而提高预测绩效上进行了系列研究。Bai和Ng提出了一种统计门限方法(Thresholding Rule)，(4)Bai,J. & Ng,S. ,“Forecasting Economic Time Series Using Targeted Predictors”,Econmetria,Vol. 146,2008,pp. 304-317.该方法通过去除与目标变量不相关的可用变量以提高预测精度，Mol等则使用贝叶斯缩减方法(Bayesian Shrinkage)进行预测。(5)Mol,C. D. ,Giannone,D. ,& Reichlin,L. ,“Forecasting Using a Large Number of Predictors: Is Bayesian Shrinkage a Valid Alternative to Principal Components? ”,Journal of Econometrics,Vol. 146,No. 2,2008,pp. 318-328.门限方法和贝叶斯缩减方法主要适用于相关信息集中在一部分可用经济变量中的情况(Non-pervasive)，如果所有的可用经济变量都包含与目标经济变量相关的信息(Pervasive)，那么这两种方法的适用性明显受限。

此外，不乏有学者开始对上述模型进行拓展，特别是将不同模型有效结合以深入分析预测能效。如：结合变量选择(variable selection)方法的桥方程(bridge model)模型、(6)Bulligan,G. ,Marcellino,& Venditti,F. ,“Forecasting Economic Activity with Targeted Predictors”,Journal of Forecasting,Vol. 31,No. 1,2015,pp. 188-206.单指标混合频率模型、(7)Kuzin,V. ,Marcellino,& Schumacher,C. ,“Pooling Versus Model Selection for Nowcasting GDP with Many Predictors: Empirical Evidence for Six Industrialized Countries”,Journal of Applied Eonometrics,Vol. 28,No. 3,2013,pp. 392-411.贝叶斯估计(8)Carriero,A. ,Clark,T. E. ,& Marcellino,M. ,“Real Time Nowcasting with a Bayesian Mixed Frequency Model with Stochastic Volatility”,Journal of the Royal Statistical Society,Vol. 178,2015,pp. 837-862.和混合频率因子模型。(9)Giannone,D. ,Reichlin,L. ,& Small,D. ,“Nowcasting GDP and Inflation: The Real-Time Informational Content of Macroeconomic Data Releases”,Journal of Monetary Economics,Vol. 55,2008,pp. 665-676.其中，Barhoumi等比较了小型桥方程和预测方程，并通过对从大量月度数据集中提取的因素进行回归来实现月度和季度数据之间的桥接。(10)Barhoumi,K. ,Darne,O,& Ferrara,L. ,“Are Disaggregate Data Useful for Factor Analysis in Forecasting French GDP?”,Working Papers,2009,pp. 132-144.Angelini等拓展了Banbura和Runstler的研究，并将预测结果与从选定的桥方程中汇集的预测结果进行比较，结果发现，在大样本预测中，因子分析法能够表现为较好的预测能效。(11)Angelini,E. ,Camba-Mendez,G. ,Giannone,D. ,Runstler,G. ,& Reichlin,L. ,“Short Term Forecasts of Euro Area GDP Growth”,Econmetrics Journal,Vol. 14,2011,pp. C25- C44.

在采用因子法预测的一支文献中，我们还发现学者将混频思想纳入因子模型之中进行拓展，即采用混频因子模型对经济变量进行预测。如：Banbura和Runstler允许非平衡数据纳入模型并实现对传统因子模型的拓展，结果发现改进后的模型对于提高预测能效具有一定的促进作用。(12)Banbura,M. ,& Modugno,M. ,“Maximum Likelihood Estimation of Factor Models on Data Sets with Arbitrary Pattern of Missing Data”,Journal of Applied Econometrics,Vol. 29,No. 1,2014,pp. 133-160.Marcellino等基于包含随机波动的贝叶斯估计框架进行预测。(13)Marcellino,M. ,Porqueddu,M. ,& Venditti,F. ,“Short-Term GDP Forecasting with a Mixed Frequency Dynamic Factor Model with Stochastic Volatility”,Journal of Business & Economic Statistics,Vol. 34,No. 1,2016,pp. 118-127.需要指出的是，上述研究的核心思想均是基于卡尔曼滤波理论进行建模预测，尽管能够表现为一定的预测绩效(power)，但当数据呈现为高频属性及大数据特征时，基于卡尔曼滤波理论的预测将会失效。为克服这一缺陷，Marcellino和Schumacher提出了一种更简单的替代方案，(14)Marcellino,M. ,& Schumacher,C. ,“Factor MIDAS for Nowcasting and Forecasting with Ragged-Edge Data: A Model Comparison for German GDP”,Oxford Bulletin of Economics and Statistics,Vol. 72,No. 4,2010,pp. 518-550.将不规则数据因素估计的期望最大化(EM)算法与Ghysels等使用的混合数据采样(MIDAS)回归技术(15)Ghysels,E. ,Gourieroux,C. ,& Jasiak,J. ,“Stochastic Volatility Duration Models”,Journal of Econometrics,Vol. 119,No. 2,2004,pp. 413-433.以及其不受限制的对象U-MIDAS结合起来。然而，需要提及的是，上述基于混频数据的因子分析所隐含的经济学含义并未得到直观解释，且对计算要求较高，特别是基于大数据集的混频模型中，上述模型并未体现较好的预测绩效。

针对上述方法所隐含的潜在缺陷，Kelly和Pruitt 对因子模型的传统设定进行拓展与改进，并创新地提出三步回归滤波法(Three-Pass Regression Filter，3PRF)，(16)Kelly,B. ,& Pruitt,S. ,“The Three-Pass Regression Filter: A New Approach to Forecasting Using Many Predictors”,Journal of Econometrics,Vol. 186,No. 2,2015,pp. 294-316.该方法通过引入代理变量(Proxy Variable)并提取出与目标经济变量相关的因子进行经济预测，可以在普适性(Pervasive)和非普适性(Nonpervasive)两种情况下使用，并进一步提高预测精度。换言之，3PRF中的代理变量可以依据经济理论进行筛选，或者通过对目标经济变量的变换进行构造，因而具有较强的理论依据及适用性。

总的来看，关于预测因子的提取及模型参数的假设，学界已从不同维度展开相应的研究并取得了富有价值的成果，这为本研究进一步对上述理论进行拓展并以此得到更为有效的预测结果提供了较好的基础。然而，我们发现上述研究还存在如下待于突破之处：第一，对于存在大量可用经济变量情况下的预测，由于可用经济变量的数目一般接近目标经济变量的样本数量，因此会导致传统的估计方法预测效果欠佳。尽管有学者在PCR模型中采用贝叶斯缩减技术去除不相关的因子以提高预测绩效，但由于相关信息相对发散，进而使得筛选出来的因子依然含有较多的不相关信息，从而导致预测绩效较差。第二，在3PRF方法的预测应用中，由于模型参数设定为常数，然而在不同的经济环境及区制下，预测因子很有可能会出现结构性变动。与此同时，由于前瞻性变量往往具有较高的频率，而3PRF方法在预测的过程中又依赖于同频数据，因而无法满足前瞻变量所呈现的时效性。第三，在上述模型的预测应用中，通常设定参数服从随机游走过程，且扰动项服从正态分布，这种假定存在局限性。在现实中，我们通常无法明确外生冲击的分布，而依赖于正态分布的假设也会导致参数估计非一致性，从而无法实现更有效的预测。

有鉴于此，本研究将对3PRF方法没有纳入不同频率预测因子的不足进行改进，并提出混频参数三步回归滤波法(Mixed Frequency Parameter Three-Pass Regression Filter，MF-3PRF)，旨在提高对目标变量的预测绩效。首先，本文提出的MF-3PRF模型允许提取的因子具有混频属性，从而弥补了3PRF模型没有考虑混频数据的结构性变化的缺陷，该模型不仅从理论上拓展了3PRF的适用范围，而且拥有更高精度的预测“势”(power)。其次，伴随着我国步入新常态以及结构转型和产业升级的现实背景，由于MF-3PRF方法考虑到了经济系统的结构性变动，预期MF-3PRF能够较为贴近现实情境，并呈现较高的预测绩效，从而可以为当局和微观经济主体的经济决策提供更为可靠的参考依据。最后，在对MF-3PRF进行参数估计时，为了克服外生冲击分布未知的情形，我们在加入系数离散变化的马尔科夫区制转换模型的基础上，进一步采用贝叶斯非参(Bayesian Nonparametric)的方法结合无限混合正态分布(Infinite Mixture Normal)对未知外生冲击的真实分布进行逼近，从而对于预测绩效的提高具有重要的理论价值与现实意义。

余文研究结构安排如下：第二部分将传统3PRF拓展为MF-3PRF形式，特别是对其理论建模进行详细概述。第三部分推算MF-3PRF的大样本渐进性质，证明其在大样本情况下会逼近最优预测；第四部分为应用分析，具体为采用混频三步回归滤波理论进行建模并对人民币汇率进行预测，特别是对比了MF-3PRF与其他备择方法的预测绩效；第五部分为本文的结论。

二、混频3PRF的理论建模

PCR方法的基本原理是从可用经济变量中提取因子，因此所提取的因子可以很好地解释经济变量的共同变化。但需要注意的是，提取出来的因子来源于可用经济变量，这并不能意味着所有的因子都和目标经济变量相关。因此，如果能够提取出和目标经济变量相关的因子无疑能够提高预测精度。Kelly和Pruitt 提出了三步回归滤波法(Three-Pass Regression Filter，3PRF)，该方法通过引入代理变量(Proxy Variable)提取出与目标经济变量相关的因子进行经济预测，并进一步提高预测精度。(17)Kelly,B. ,& Pruitt,S. ,“The Three-Pass Regression Filter: A New Approach to Forecasting Using Many Predictors”,Journal of Econometrics,Vol. 186,No. 2,2015,pp. 294-316.特别地，在3PRF模型中，其模型设定形式具体如下：

(1)

zt=λ0+ΛFt+ωt

(2)

xt=φ0+ΦFt+εt

(3)

诚如前文所言，当大型数据集xt的驱动因素超过目标变量yt时，其渐进性和强因子结构特征并不会对预测结果产生明显影响。对于式(1)而言，当样本有限时，也即当ft较弱而gt较强时，使用和式(1)中所需的ft因子则相对有效。为此，Kelly和Pruitt针对ft的估计提出了如下简易且有效步骤，(19)Kelly,B. ,& Pruitt,S. ,“The Three-Pass Regression Filter: A New Approach to Forecasting Using Many Predictors”,Journal of Econometrics,Vol. 186,No. 2,2015,pp. 294-316.具体如下：

第一步：在zt上对xt中的每个元素xi,t进行时间序列回归，即：

(4)

(5)

对每一个t=1,…,T，我们保留了t的OLS估计值。

yt=β0+β′t-1+ηt，t=1,…,T

(6)

(7)

由于本文所关注的对象是当目标变量yt(或代理变量zt)的频率低于xt的频率时，其抽样预测绩效呈现怎样的特征。进一步地，我们允许xt的分量(quantile)仅在低频下有效，并假设xt中存在“不规则边缘”的形式，并用τ表示聚合(低)频率，用L表示高频滞后算子t，用Z表示低频滞后算子τ，且由Z=Lk可得Zyτ=yτ-1。

为体现时间聚合的特征，我们引入算子，

ω(L)=ω0+ω1L+…+ωk-1Lk-1

(8)

其中，对于代理变量zτ，有zτ=ωLzt。对于xt中的每一个高频指标，xi,t满足xi,τ=ω(L)xi,t，τ=1,2,…,T/3(此处τ以低频为单位，所以τ=1相当于t=aτ，a=2,3,4,…，i=1,…,N。)运用上述定义的变量，我们首先基于低频(季度)τ，在zτ上对xτ中的每个元素xi,τ进行时间序列回归，具体如式(9)所示：

(9)

(10)

对于每个高频(月度)t=1,…,T，我们保留了t的OLS估计值。

(11)

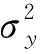
为体现时间聚合后模型所呈现的静态特征，本文对代理变量zt进行时间聚合来刻画xt高频性质。特别地，如果松弛参数ω(L)大于聚合频率k，聚合模型的误差将呈现序列相关性，但并不影响条件期望的静态特征。然而需指出的是，如果采用ω1(L)表示zt的滞后，而用ω2(L)表示xt中其他元素的滞后，则时间聚合模型中可能存在动态因素，此时误差项中也会存在序列相关。因此，在静态聚合回归模型中对斜率系数的估计，即在zτ上对xiτ的回归，其参数估计结果将呈现非一致性，这将对预测结果的准确性产生影响。

为进一步刻画时间聚合性质，我们将预测重新表达为：

(12)

(13)

(14)

(15)

诚如前文所言，我们可以利用3PRF得出其二阶段系数，具体如式(16)所示：

(16)

进一步将参数和因子依概率收敛的形式表示如下：

(17)

(18)

(19)

(20)

xi,t=φ0,i+z*′tφi+vt+γi,t，t=1,…,T

(21)

再次用OLS进行估计，由于误差项为vt+γi,t，此时参数φi的估计值所具有的有效性将低于3PRF第一步估计值的有效性，但依然与其保持一致、无偏，且服从渐进正态分布。

总的来看，MF-3PRF保持了3PRF每一阶段参数估计一致性的特点。然而，诚如前文所言，MF-3PRF在有限样本中与3PRF相比存在渐进性的差异。因此，为了体现MF-3PRF在实时预报和短期预测实证应用中所呈现的能效，我们还对其有限样本属性进行模拟。

三、混频3PRF的样本性质分析

在对混频3PRF的样本性质进行研究时，我们主要依据蒙特卡罗模拟技术对混频3PRF在样本有限情况下的预测精确度进行检验。我们的模拟分析主要从其样本外预测的结果和与其他三种备选预测方法(分别为DMA、DMS、TVP-VAR、BMA模型)的比较来展开。其中，依据Primiceri、Korobilis的研究，(20)Primiceri,G. E. ,“Time Varying Structural Vector Autoregressions and Monetary Policy”,The Review of Economic Studies,Vol. 72,No. 3,2005,pp. 821-852.(21)Korobilis,D. ,“ VAR Forecasting Using Bayesian Variable Selection”,Journal of Applied Econometrics,Vol. 28,No. 2,2013,pp. 204-230.设定TVP-VAR模型形式如下：

yt=ztθt+εt

(22)

θt=θt-1+ηt

(23)

其中，yt表示在t时刻的人民币对美元汇率，zt=[1,xt-1,yt-1,…yt-p]表示预测因子，θt=[φt-1,βt-1,γt-1,…γt-p]为系数向量。式(22)、(23)所体现的一个优点在于系数具有时变特性。为减少因冗余参数而对模型参数估计所造成的负面影响，Hoogerheide等(22)Hoogerheide,L. ,Kleijn,R. ,Ravazzolo,F. ,Van Dijk,H. K. ,& Verbeek,M. ,“Forecast Accuracy and Economic Gains from Bayesian Model Averaging Using Time-Varying Weights”,Journal of Forecasting,Vol. 29,2010,pp. 251-269.进一步将TVP-VAR模型表示如下：

(24)

其中，yjt表示从j个模型中预测的结果，K表示总共的模型个数，θjt表示时变权重。此外，我们在采用式(24)中的TVP-VAR模型对人民币汇率进行预测时，主要采用两种形式：第一种为包含截距项及汇率与预测因子均为时变参数；第二种是包含截距项及仅人民币汇率存在滞后项，而预测因子不存在滞后项。

(25)

(26)

为较好地进行描述，我们将DMA/DMS分别引入单一模型和多重模型进行阐释。在既定的Ht与Qt下，卡尔曼滤波可被用来进行递归估计及预测。我们将卡尔曼滤波的初始及进程表述如下：

θt-1yt-1～N(θ′t-1,Σt-1t-1)

(27)

θtyt-1～N(θ′t-1,Σt-1t-1)

(28)

其中，Σtt-1=Σt-1t-1，我们此时引入遗忘因子λ(0≤λ≤1)，此时我们得到：

(29)

同样，我们也可得到：

θtyt～N(t,Σtt)

(30)

其中，

(31)

(32)

我们进一步采用如下预测分布来实现递归预测，具体如下：

(33)

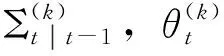
(34)

(35)

(36)

此外，我们还根据Raftery 等的研究，将遗忘因子纳入到转移矩阵之中，并设定两个遗忘因子α,γ(0≤α≤1,0≤γ≤1)。本文设定两个遗忘因子α,γ⊂(0.95,0.99)。

如前文所述，在进行预测的过程中，实际上隐含着Lt=k的条件，接下来我们进一步在模型中引入遗忘因子α以分析无条件的预测。值得注意的是，在预测方程中引入遗忘因子时，我们不再需要马尔科夫链蒙特卡罗模拟进行不同模型之间的转换。依据卡尔曼滤波，当观测信息已知时，我们可通过如下DMA方式获取结果：

(37)

其中，令πts=p(Lt=lys)，此时我们可将p(Lt-1=k,yt-1)重新写为πt-1t-1,k，对于无约束的转移矩阵而言，我们可将其元素pkl写为：

(38)

进一步根据Raftery等的研究，(29)Hansen,P. R. ,“ A Test for Superior Predictive Ability”,Journal of Business & Economic Statistics,Vol. 23,No. 4,2005,pp. 365-380.在上式中纳入另一个遗忘因子α(0≤α≤1)，并以此构建DMA模型的参数，因此式(38)可以重新写为：

(39)

因此，我们可将更新之后的模型写为：

(40)

其中，pl(ytyt-1)为模型l下对yt的预测密度。进一步，我们采用πtt-1,k对每个模型的预测结果进行平均，因此基于模型平均法对汇率yt的预测前1期可表示如下：

(41)

值得注意的是，DMS是通过对单个模型的πtt-1,k进行比较，并在每个点上选择其最大值用来预测，因此DMS可看作DMA的一个特例。而对于遗忘因子α而言，当α=0时，所有模型具有相同的权重，而当α=1时，则意味着BMA模型可视为DMA模型的特例。ft=ρfft-1+uf,t表示在第i个观察值之前呈现指数型衰减。在本文的研究中，我们所设定的α∈(0.95,0.99)略小于1，能够较好地预测人民币对美元汇率。此外，我们还对TVP-VAR模型在遗忘因子λ=0.99以及λ=0.95(作为DMA/DMS的特例)等不同的情况下进行了检验。

(42)

(43)

当然，在对模型进行预测时，尽管损失函数可以被用来判断模型在预测方面的绩效，但并不能分辨出该模型是否显著优于其他模型。举例而言，当采用MAFE作为判断标准时，如果模型甲比模型乙的预测损失值小，只能判断在这样一个特定的数据样本中，采用该特定损失函数时，模型甲比模型乙的预测精度高。很明显，这一判断是不稳健的，且无法推广到其他类似的数据样本或者其他的损失函数判断标准。值得注意的是，数据样本中存在的少数奇异点往往会严重影响损失函数的计算结果，从而引起损失函数值异常增加，进而可能导致对模型优劣的错误判断。

基于此，Hansen提出了采用高级预测能力检验法(Superior Predictive Ability, SPA)来比较分析多步预测的能力。(30)Hansen,P. R. ,“ A Test for Superior Predictive Ability”,Journal of Business & Economic Statistics,Vol. 23,No. 4,2005,pp. 365-380.需要提及的是，虽然SPA模型比传统的损失函数具有一定的优越性，但它必须要求存在基准模型时才能进行比较，极易产生与对照组的多重比较问题。此外，SPA的原假设是复合假设，不仅会影响SPA检验统计量的渐进分布，还会出现过度参数化的问题，从而很容易拒绝正确的原假设。为克服这一缺陷，Hansen等提出了模型可信集检验法(Model Confidence Set, MCS)，该统计量能够较好地克服SPA等统计量所存在的缺陷，而且不需要选择基础模型，因此使得检验结果更具稳健性和外延性。(31)Hansen,P. R. ,Lunde,A. ,& Nason,J. M. ,“The Model Confidence Set”,Econometrica,Vol. 79,No. 2,2011,pp. 453-497.对于MCS统计量而言，其原假设为所有模型具有相同的预测能力，且主要包含两个统计量，分别为范围统计TR与半二次方统计量TSQ，具体表达如下：

(44)

(45)

(46)

我们使用N=T=100或N=T=200的两个数据集进行模拟，其样本外预测结果见表1所示。特别地，在构造参数的过程中，我们进行5 000次模拟抽样，并将因子结构强度划分为三个类别：第一类为“正常因素”，其预测因子的百分比中值R2为30%；第二类为“中偏弱因素”，其R2为20%；第三类为“弱因素”，其中R2为10%。其中，正常因子结构与Stock 和 Watson对宏观经济数据的分析中所提到的共同因素变化的程度相一致。(35)Stock,J. ,& Watson,M. ,“Forecasting Using Principal Components from a Large Number of Predictors”,Journal of the American Statistical Association,Vol. 97,2002,pp. 1167-1179.参照Groen 和Kapetanios 以及Onatski的研究，(36)Groen,J. J. ,& Kapetanios,G. ,“Model Selection Criteria for Factor-Augmented Regressions”,Oxford Bulletin of Economics and Statistics,Vol. 75,No. 1,2013,pp. 37-63.(37)Onatski,A. ,“Asymptotics of the Principal Components Estimator of Large Factor Models with Weakly Influential Factors”,Journal of Econometrics,Vol. 168,No. 2,2012,pp. 244-258.我们对“中偏弱”因子结构进行相应的设定。需要注意的是，由于因子载荷量在模拟过程中呈现潜在的随机性特征，因此，受其自身异质性的影响，各预测因子对目标变量的预测绩效也表现为明显差异。特别地，在上述三类别中，本文模拟所有预测因子载荷量非零。对于“中偏弱非普适因素”而言，由于相关因素不具有普适性，我们将其中一半的预测因子对相关因素的因子载荷量设置为零。

表1 样本外模拟预测绩效

蒙特卡罗模拟结果表明，单因素混频3PRF相较于其他因素而言，在不同参数下均表现出较好的预测绩效。事实上，PCR5和PCLAR的预测绩效也在部分情形下优于混频3PRF的预测绩效，但其优势相对较弱。特别地，在较大的样本中，强因子结构的情况下，因子会迅速恢复至均值水平，且特征异质性预测因子之间几乎没有序列或截面相关性。此外，混频3PRF的能效往往远远超过其他方案，尤其是小样本情况下弱因子结构的情况。此外，混频3PRF的预测全部基于单一的估计因子，而备择方案则在其预测方程中使用5或10个因子。由此，预测因子中的不相关因素对PCR5和PCLAR的预测绩效产生了不利影响。

四、基于MF-3PRF模型的人民币汇率预测

(一)预测因子筛选

接下来，本文将采用MF-3PRF方法对人民币汇率的动态变化特征及波动成因再检验。需要注意的是，从理论上来看，有关决定或影响汇率水平及变动因素在学术上已产生了经典理论，其中，购买力平价理论、利率平价理论是汇率决定的重要理论基础，同时，弹性价格货币模型、粘性价格货币模型与巴拉萨—萨缪尔森汇率模型将购买力平价理论与货币数量论结合，形成由货币供给、国民收入、利率和物价等基本面因素共同决定的汇率决定模型。(38)Frenkel,J. A. ,“A Monetary Approach to the Exchange Rate: Doctrinal Aspects and Empirical Evidence”,The Scandinavian Journal of Economics,Vol. 78,No. 2,1976,pp. 200-224.(39)Dornbusch,R. ,“Expectations and Exchange Rate Dynamics”,Journal of Political Economy,Vol. 84,No. 6,1976,pp. 1161-1176.而且由于泰勒规则综合了维克塞尔(Wicksell)的累积过程学说、费雪效应、传统货币数量论、凯恩斯货币理论及弗里德曼现代货币数量论等思想而形成了一个新的货币政策规则，因此，较多的学者开始采用泰勒规则汇率模型解释汇率变动。(40)Frankel,J. A. ,“On the Mark: A Theory of Floating Exchange Rates Based on Real Interest Differentials”,The American Economic Review,Vol. 69,No. 4,1979,pp. 610-622.(41)Frankel,J. A. ,“In Search of the Exchange Risk Premium: A Six-Currency Test Assuming Mean-Variance Optimization”,Journal of International Money and Finance,Vol. 1,1982,pp. 255-274.(42)Mark,N. C. ,“Exchange Rates and Fundamentals: Evidence on Long-Horizon Predictability”,The American Economic Review,Vol. 85,No. 1,1995,pp. 201-218.(43)Groen,J. J. ,“The Monetary Exchange Rate Model as a Long-Run Phenomenon”,Journal of International Economics,Vol. 52,No. 2,2000,pp. 299-319.(44)Mark,N. C. ,& Sul,D. ,“Nominal Exchange Rates and Monetary Fundamentals: Evidence from a Small Post-Bretton Woods Panel”,Journal of International Economics,Vol. 53,No. 1,2001,pp. 29-52.(45)Engel,C. ,& West,K. D. ,“Exchange Rates and Fundamentals”,Journal of Political Economy,Vol. 113,No. 3,2005,pp. 485-517.为此，本文沿袭经典理论，重点选择了无抛补利率平价、购买力平价、弹性价格模型、粘性价格模型、巴拉萨—萨缪尔森模型、资产组合平衡模型以及泰勒规则汇率决定理论模型进行比较分析。借鉴江春等的研究，(46)江春、杨宏路、李小林: 《基于泰勒规则的人民币汇率预测研究: 兼论多种汇率决定模型预测比较》,《世界经济研究》2018 年第4 期。本文在对人民币汇率进行预测时，所依据的理论模型及基础预测因子选择整理如表2所示。

表2 理论模型及预测因子选择

(二)变量选取及相关检验

结合前文理论分析并借鉴经典文献中变量的度量形式，对于人民币汇率而言，本文采用直接标价法下的人民币对美元即期汇率(ER)，由于美国的联邦基金利率被视为最能够灵敏地反映银行之间的资金短缺情况及资金供求状况的基准利率，因此采用美国联邦基金利率(if)作为美元利率的代理指标。相应地，人民币利率采取中国银行间同业拆借隔夜利率(id)，同样，中美两国的通胀水平分别采用中国和美国的消费者价格指数的同比增长率(πd和πf)来衡量，而中美两国物价水平则采用居民消费者价格指数(CPId和CPIf)表示。此外，对于产出而言，由于中国没有对月度GDP进行统计，因此我们采用季度GDP增长率衡量产出，同时我们对GDP增长率进行HP滤波处理，从而得到产出增速缺口，因此中美两国产出缺口之差采用两国GDP增速缺口之差进行表示。最后，对于生产率而言，我们借鉴Cheung等的研究，(47)Cheung,Y. W. ,Chinn,M. D. ,& Pascual,A. G. ,“Empirical Exchange Rate Models of the Nineties: Are Any Fit to Survive? ”,Journal of International Money and Finance,Vol. 24,No. 7,2005,pp. 1150-1175.采用人均GDP增长率进行测度。而对于资产价格而言，我们采用股票市场综合价格指数进行衡量。紧接着，我们将除利率及通胀之外的其他原始时间序列数据全部进行X-12季节调整及自然对数处理，并在此基础上最终求得中美两国的股价之差(SP)、息差(ID)、通货膨胀之差(CPI)及产出缺口差(GDP)。上述数据来源于OECD数据库、美国St.Louis联邦储备银行数据库、FRED及Wind数据库，其中月度数据样本期间为2005年7月至2018年12月，而季度数据样本期间为2005年第3季度至2018年第4季度。

表3为本文研究变量的描述性统计结果。从该表中不难发现，股价的标准差最大，为33.582，意味着股票市场价格波动最为剧烈，而汇率的标准差最小为0.091，意味着人民币汇率的波动相对较小。从J-B统计量中可以看出，除股价差与央行外汇干预之外，其余所有变量均在既定的显著性水平下拒绝了“存在正态分布”的原假设，意味着股价差与央行外汇干预为正态分布，而其余所有变量均服从偏态分布。同时从偏度可以看出，除汇率、产出差、央行外汇干预与汇率预期大于0之外，其余变量均小于0，意味着汇率、产出缺口差、央行外汇干预及汇率预期服从右偏分布，而其余变量均服从左偏分布。

表3 描述性统计结果

在对变量间的关系进行刻画时，为避免出现虚假回归并导致参数估计结果出现非一致情形，而且考虑到本文所涉及的经济金融变量易受非预期外部冲击及政策调整的影响而具有结构突变特征，特别是在不同的时间区间及区制环境下，上述变量的动态变化特征很有可能存在分异。鉴于此，我们借鉴司登奎等的研究，(48)司登奎、李小林、张仓耀: 《分位数单位根检验的拓展及其应用研究》,《统计研究》2017 年第5 期。采用能同时捕捉结构突变和平滑渐变的分位数单位根方法对变量的非线性动态变化进行平稳性检验，结果如表4所示。

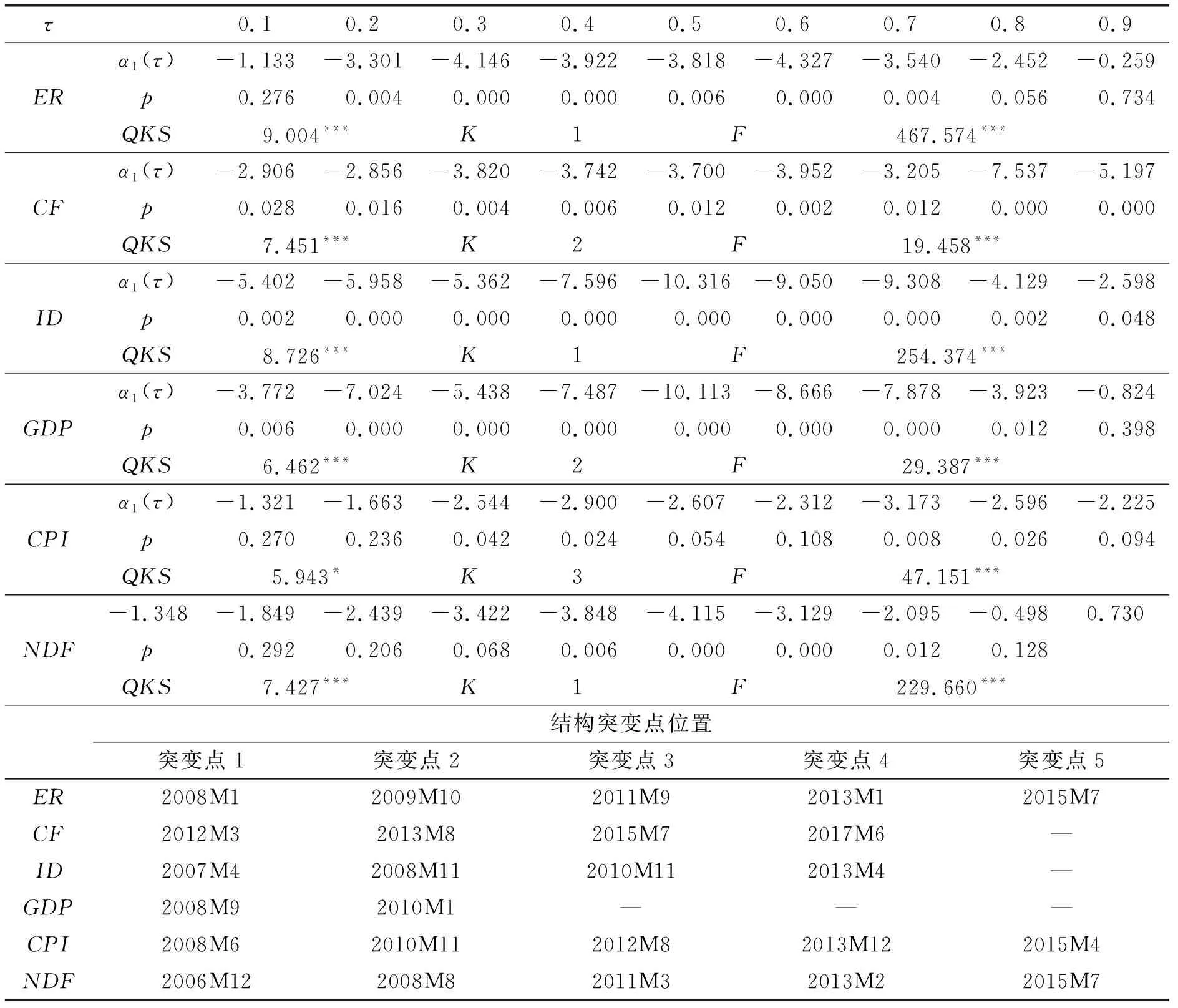
表4 含结构突变与平滑渐变点的分位数单位根检验结果

从表4中的检验结果可以看出，QKS统计量在至少10%的显著性水平下拒绝了“序列为非平稳”的原假设，这意味着上述所有变量均为平稳序列。从平滑渐变点检验结果(K)可以发现，中美通胀差含有3个平滑渐变点，国际资本流动与产出缺口均含有2个平滑渐变点，而汇率、中美利差及汇率预期均含有1个平滑渐变点。同时，结构突变点检验结果表明，人民币即期汇率、中美通胀差及汇率预期均含有5个结构突变点，资本流动、利差均含有4个结构突变点，而产出缺口差则含有2个结构突变点。此外，所有变量的F统计量在至少10%的显著性水平下拒绝了“变量为线性”的原假设，这意味着变量的数据生产过程(Data Generating Process，DGP)均呈现非线性特征，这在一定程度上印证了采用非线性方法刻画变量间的动态关系的必要性。

考虑到单一模型不能兼顾不同经济状态下人民币汇率的变动特征，进而使得预测结果面临较大的不确定性。为克服这一不足，我们联合采用DMA、DMS、TVP-VAR及BMA模型进行预测。需要注意的是，不同的预测长度也会影响模型的预测能力，因此本文选择了预测步长为1、2、3、6、12，并予以比较分析，旨在考察究竟哪种模型具有较好的预测绩效。

(三)实证结果及分析

结合上述理论模型中的预测因子，我们进一步采用多种计量模型对人民币汇率进行联合预测，并采用MAFE与MSFE的损失函数来比较相应的预测精度，其中MAFE与MSFE值越大意味着预测精度越差，同时也表明该模型的预测能力较弱。从表5中的预测结果不难发现，在所有的计量模型与理论模型中，MF-3PRF具有较小的预测误差(MAFE与MSFE)。同时仍需注意的是，在本文所采用的多种计量模型对汇率进行预测时，并非所有模型均优于随机游走(RW)模型，如：TVP-VAR(2)-X的MAFE与MSFE均大于RW模型，而DMA模型则优于RW模型，且MF-3PRF模型在对人民币汇率预测精度上优于DMA(0.95，0.95)。值得注意的是，MF-3PRF模型预测的MAFE与MSFE值要小于其他情况下计量模型预测的MAFE和MSFE值，原因在于MF-3PRF模型对最佳方程外的其余方程所赋予的权重为0，而且由于MF-3PRF模型具有简约特性且能够充分利用混频先行指标的时效性，能够有效避免过度识别的问题，这也进一步使得MF-3PRF模型表现出较高的预测绩效。

表5 不同模型的预测精度比较

(续上表)

诚如前文所言，尽管MAFE与MSFE能够比较出不同模型对人民币汇率的预测能力，但无法辨析出哪种模型显著最优。鉴于此，我们进一步参照Hansen等所提出的模型可信集(MCS)检验方法，(49)Hansen,P. R,Lunde,A. ,& Nason,J. M. ,“The Model Confidence Set”,Econometrica,Vol. 79,No. 2,2011,pp. 453-497.并在不同理论与计量模型下对人民币汇率的预测精度进行比较，结果如表6所示。从表6中容易发现，MF-3PRF模型在预测人民币汇率变动时，在所有的预测步长内，其MCS检验的伴随概率在所有模型中最大且均大于0.1，表明MF-3PRF模型是模型可信集检验过程中幸存的模型，其P值越大表明该模型的预测精度越高，也即表明MF-3PRF模型是预测能力较好的模型。因此，我们可以判定包含内生特征的泰勒规则模型能够较好地解释人民币汇率变动，同时MF-3PRF模型在预测人民币汇率变动上表现出了较高的预测能力，这也进一步表明运用MF-3PRF结合考虑了具有内生特征的泰勒规则汇率模型能够较好地解释人民币汇率变动的趋势，而且图1中MF-3PRF的MSFE与备择模型MSFE比值的动态变化趋势也进一步印证了上述结论。

表6 不同模型的MCS检验

(续上表)

五、结论

本文将混频思想纳入3PRF理论之中并提出混频三步回归滤波法(Mixed Frequency Three-Pass Regression Filter，MF-3PRF)，从而实现提高预测绩效的目的。特别地，本文提出的MF-3PRF模型允许提取的因子具有混频属性，能够解决3PRF模型没有考虑混频先行指标时效性的缺陷。基于样本性质的理论模拟结果表明，MF-3PRF不仅能够保持传统3PRF的有效性与一致性，表现出较高的理论预测绩效，而且，当经济系统呈现结构性变动时，MF-3PRF呈现较优的预测能效，因而具有较强的适用性。

进一步地，文章基于MF-3PRF模型结合备择模型(DMA、DMS、TVP-VAR、BMA、RW)并选取无抛补利率平价、购买力平价、弹性/粘性价格货币模型、巴拉萨—萨缪尔森模型、资产组合模型、泰勒规则等理论模型对人民币汇率进行预测，结果表明无抛补利率平价模型、购买力平价模型、弹性价格货币模型、粘性价格货币模型、巴拉萨—萨缪尔森效应模型、资产组合模型对人民币汇率均具有一定的预测能力，但多种计量模型均表明其预测能力低于随机游走模型。而当采用泰勒规则模型对人民币汇率进行预测时，其样本外预测能力显著高于随机游走模型。同时，在采用MF-3PRF、DMA、BMA以及TVP-VAR等多种模型进行预测时，MF-3PRF模型具有较好的预测绩效。鉴于MF-3PRF并结合泰勒规则能够较好地捕捉人民币汇率的动态变化特征，因而能为货币当局稳定人民币汇率以及公众在新的汇率形成机制条件下深入认识人民币汇率动态变化与波动成因提供启示。