发展学生数学核心素养的实践与认识
2020-05-14刘荣坤
摘 要:“发展学生的核心素养”已经成为高中数学教学的中心任务,教师要从学生的长远发展角度出发,切实优化教学环境,促使学生实现可持续发展。直观想象素养关系着高中生空间观念的形成,本文将从动手操作积累直观想象经验、借助实物拓展直观想象空间、数形结合提炼直观想象内涵、综合应用发展直观想象能力这四个维度来分析课堂教学中发展学生数学核心素养的实践与认识。
关键词:高中数学;直观想象;实践与认识
直观想象素养是指通过图形与几何知识去探究事物之间的空间形式,积极迁移空间与几何知识来分析空间形态与运动规律的一个数学素养,比如学生利用空间观念去确定事物位置、以图形运动去描述现实问题、以数形结合思想去解决问题等多种思维表现。直观想象水平是衡量高中生理解数学的难易程度及数学探究能力高低的重要指标。因此,课堂教学中要寻求发展学生直观想象素养的切实有效的途径与策略。
一、 动手操作积累直观想象经验
高中数学教学一直都是以教师讲授数学知识为基本形式的,这种教学行为有效地增加了课时容量,可以提高学生的应试成绩,但却难以提高学生的独立思考能力。培养学生的直观想象能力,首先便是要积累直观想象经验,切实把握常见的空间形式与结构变化规律。因此要鼓励学生动手操作,如绘制几何图形、利用几何画板观察图形变化,制作几何模型等。
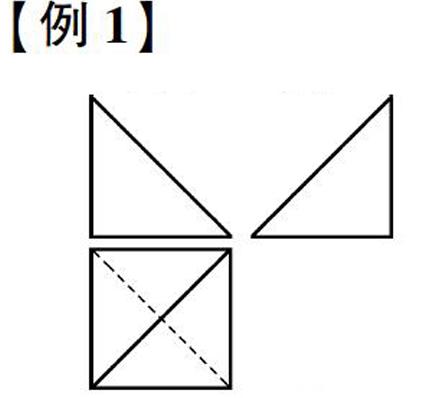
【例1】 已知某几何体的三视图如图所示,正视图和侧视图均是腰长为1的等腰直角三角形,俯视图是边长为1的正方形,则该几何体外接球的体积为_____。
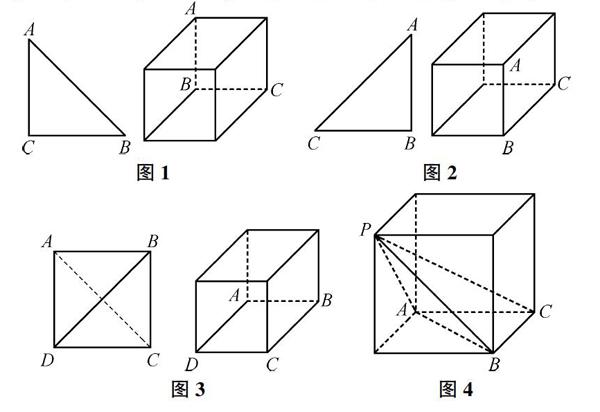
分析:首先要根据三视图画出几何体的直观图,大部分学生都有畏难心理。解决三视图问题,尤其是一些比较复杂的三视图还原问题,需要极强的空间想象能力。我们可以用一个正方体作为载体对三视图进行还原。
如图1,画出正视图的三个顶点的原象所在的线段,用粗线表示,即正视图的三个顶点必定由图中粗线上的点投影生成;如图2,侧视图中的三个顶点必定由图中粗线上的点投影生成;如图3,俯视图中的四个顶点必定由图中粗线上的点投影生成。三个图中三条粗线的交点即为原几何体的顶点,如图4。
教师用几何画板进行示范,然后让学生动手操作。通过动手操作,激发学生的学习兴趣,引起学生内心成功解决问题的渴望。在生生互动、师生互动中引导学生在“互辩”中寻求最佳方案,使学生的探究意识在不断循环和矛盾中得到强化。通过练习反思,学生能够掌握还原几何体的基本思路和方法,积累直观感知的经验。
二、 借助实物拓展直观想象空间
高中数学教学以教材知识为中心,教师很少会利用生活资源来解释数学知识,学生也不会主动利用数学所学去解释生活现象、探索生活问题。凭空想象可能会引起学生的相异构思,如果借助生活实物来展示事物的空间形状与结构特点,让学生少走弯路,会起到事半功倍的作用。
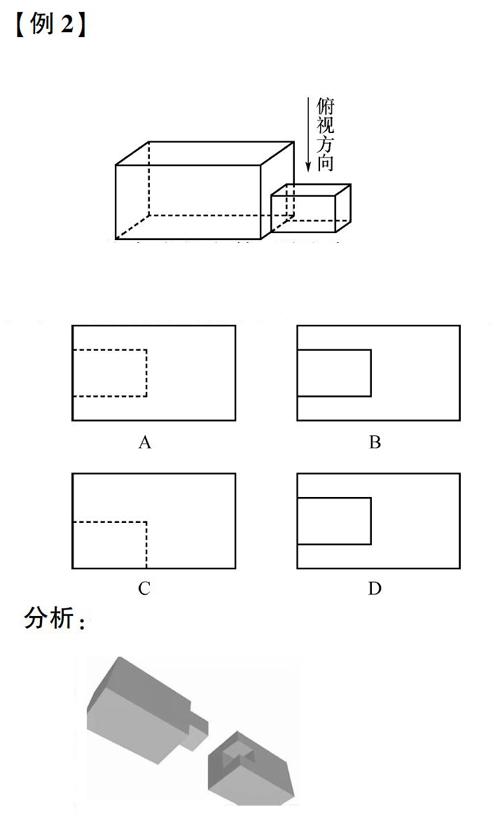
【例2】 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件左边的小长方体是榫头。若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()
分析:心理学研究表明人的抽象思维经“具体→形象→抽象”这三个过程,若实际经验太少,或识图水平较低,就难以理解三视图的几何意义,更难以通过三视图还原直观图。借助如图所示的实物,观察实物的几何结构和空间位置,学生通过探究、比较、反思、感受榫卯将木构件连接起的中华传统伟大工艺,拓展了学生直观想象的空间。
三、 数形结合提炼直观想象内涵
数形结合的思想,其实质是将抽象的数学语言与直观的图像结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化。培养学生直观想象素养需要数形结合思想参与问题解决。
【例3】 如图,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥平面ABCD。在线段AB上是否存在一点E,使平面PDE⊥平面PAC,如果存在,说明点E的位置;如果不存在,说明理由。
分析:在线段AB上存在点E,使平面PDE⊥平面PAC。因为PC⊥平面ABCD,所以PC⊥DE。当DE⊥AC时,有DE⊥平面PAC。又DE平面PDE,所以平面PDE⊥平面PAC。
要确定点E的位置,对于平面几何知识比较薄弱的学生就束手无策了。教师要引导学生采用建系的方法解决问题。以C为原点,CD,CB,CP分别为x,y,z轴,建立空间直角坐标系Oxyz,则A(2,1,0),B(0,3,0),D(2,0,0)。设E(x,y,0),AE=λAB,则(x-2,y-1,0)=λ(-2,2,0),故E(2-2λ,1+2λ,0),DE=(-2λ,1+2λ,0),CA=(2,1,0)。由DE⊥CA,所以DE·CA=0,即-4λ+1+2λ=0,λ=12,故E(1,2,0),因此E為AB的中点。
建系解决立体几何问题,把几何问题转化为代数问题是数形结合思想的具体应用,把较难感知的几何直观问题转化为较容易操作的代数运算问题也是直观想象素养的内涵表征。
四、 综合应用发展直观想象能力
图形演示可以将抽象、枯燥的文字转化成图形,给学生带来直观的视觉感受,由此简化数学问题的抽象度,便于学生进一步展开数学探究。因此,教师要有意识地培养学生用图、识图的能力,丰富学生的读图经验,促使学生养成良好的空间想象能力,提升学生的直观想象素养。当然也有一部分学生不善于直观想象而无法展开几何推理,所以会采用代数方法去分析解决数学问题,这也是直观想象素养的逆向表现。
【例4】 锐角三角形ABC中,角A,B,C的对边分别为a,b,c,△ABC的面积为S。若sin(A+C)=2Sb2-c2,则角C的取值范围是 。
错解:由sin(A+C)=2Sb2-c2,得sinB=acsinBb2-c2,
即b2-c2=ac。cosC=a2+b2-c22ab=a+c2b>b2b=12,∴0 学生错解的原因是忽略了锐角三角形这一条件。事实上若能把握b2-c2=ac即b2=c(c+a)的几何意义,则问题将变得非常简单。如图所示:延长AB到D使BD=a,连接CD,易得△ACB相似于△ADC,故∠D=∠ACB,所以∠ABC=2∠D=2∠ACB。因此B=2C,A=π-3C。由0<2C<π2,0<π-3C<π2,得π6 正解:因為△ABC为锐角三角形,所以b2+c2>a2,b2+a2>c2,a2+c2>b2。由上可知b2-c2=ac,代入三个不等式得c 若能把一个复杂的抽象的数学问题直观化、具体化,变抽象为形象,直观想象把握数学问题的本质,解法将会简捷优美。 五、 结语 1. 《普通高中数学课程标准(2017年版)》指出直观想象是借助几何直观和空间想象感知事物的形态和变化,利用空间形式特别是图形,理解和解决数学问题的素养。利用直观想象解决平面几何问题和空间几何问题只是直观想象素养的浅层表征,经过实物展示和动手操作训练,能够提升学生的直观感知和识图技能,提高学生的直观想象能力。事实上,直观想象更注重的是建立数学中的代数与几何的联系,几何问题可以通过建立直角坐标系或通过向量转化为代数问题,代数问题也可以建立模型回归为几何问题,这是直观想象素养的核心含义,是数学课堂教学的重要课题。 2. 几何直观是数学语言的一种翻译,是个性化的特殊数学语言,把数学问题转化为几何直观是学生自主建构的过程。在这个建构过程中,由于学生学习风格的多样性以及数学活动经验积累的程度不同,可能导致学生几何直观想象上的偏差。例5:数列{an}的通项公式为an=n2-kn,若{an}为递增数列,求k的取值范围。很多学生的答案是:k2≤1即k≤2。究其原因,学生把数列看成一般的函数,利用函数的单调性得出答案。学生在思考时遗漏了k2>1且2-k2>k2-1,即2 3. 直观想象与合情推理一样,是数学问题的提出、寻找数学问题解决的有效方法。直观想象不是万能的,不能代替文字叙述,也不能代替逻辑推理。如例5用定义解题如下:因为{an}为递增数列,所以an+1>an,即(n+1)2-k(n+1)>n2-kn,也就是k<2n+1对任意的正整数恒成立,故k<3,逻辑推理的威力可见一斑。直观想象、数形结合是学习数学、解决数学问题的有力工具,但在教学过程中应当尽可能地通过多元化的教学方式和手段引导和培养学生的直观想象素养,促进学生数学思维能力的发展。 总之,在高中数学教学中培养学生的直观想象素养可以切实展现学生利用几何与空间知识解决现实问题的思维能力。因此,高中数学教师要以丰富的动手操作、实物探索、数形结合、读图识图等活动发展学生的直观想象素养,将直观想象与逻辑推理结合起来,优化学生的思维品质。 参考文献: [1]刘春林.落实高中生数学直观想象素养的教学研究[D].石家庄:河北师范大学,2018. [2]孙亚群.高一学生直观想象素养的现状调查研究[D].福州:福建师范大学,2018. [3]王欢.基于“直观想象”素养的高中数学教学设计研究[D].重庆:重庆师范大学,2018. 作者简介: 刘荣坤,福建省福安市,福建省福安市第一中学。
