不同温度下晶面衍射弹性常数的两相模型计算

许海峰 ，祝昌军 ，陈康华 ，刘力

(1. 中南大学 轻合金研究院，长沙 410083；2. 中南大学 轻质高强结构材料国防科技重点实验室，长沙 410083；3. 中南大学 有色金属先进结构材料与制造协同创新中心，长沙 410083)

材料在服役期间受到各种复杂的应力加载，使内部产生残余应力。残余应力会影响材料的服役性能，有时甚至会带来安全隐患，因此分析材料内部残余应力情况成为研究材料力学性能的重要一环。目前衍射法探测材料残余应力的成熟手段有X射线衍射测量和中子衍射测量[1]。衍射法测量材料的残余应力是利用材料相关的晶面衍射弹性常数，结合胡克定律计算得到材料的残余应力。晶面衍射弹性常数通常通过相关实验设备测定，用理论模型计算材料的晶面衍射弹性常数相对较少，目前的研究方法例如Kroner方法[2]，往往都是将材料看做某一相的单相材料，而实际上多相材料的某一相在材料中显然会受到其他相的影响，所以将材料作为某一相的单相材料来处理，对后续的理论计算等均有不同程度的影响。除此之外，实验测定的晶面衍射弹性常数大多是常温下的，高温下的晶面衍射弹性常数研究的报道很少，主要原因在于开展相关实验的条件苛刻。对于在高温条件下服役的工程合金，若要测量高温环境下材料内部的残余应力情况等信息，需要获得材料在高温下的晶面衍射弹性常数。本文作者为了解决在高温条件下材料晶面衍射弹性常数较难测试的问题，以高温镍基合金为研究对象，将其看成是基体相γ相和γ′相的两相复合材料，以准谐德拜模型[3]和第一性原理为基础，结合现已成熟的Eshelby等效夹杂模型[4]，建立计算不同温度条件下材料晶面衍射弹性常数的两相模型。通过模型的计算，得到高温镍基合金在不同温度下的晶面衍射弹性常数，并将其与文献报道的实验测定值进行对比，验证模型的准确性。通过此模型，可预测相关复合材料在不同温度下的晶面衍射弹性常数，以便于进一步计算材料内部的残余应力，研究材料在不同温度下相关的力学性能。

1 两相复合材料晶面衍射弹性常数的模型构建

1.1 研究背景

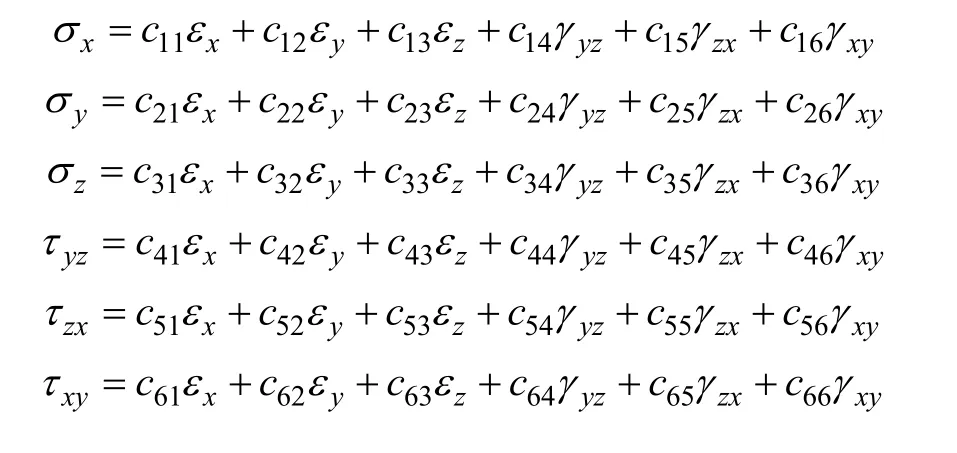
弹性常数为表征材料弹性性能的量，是用来联系应力-应变关系的一组独立的常数。材料在弹性范围内，某一点的应力状态和应变状态分别可用6个独立的分量表示，6个应力和6个应变在弹性范围内可用以下的线性关系式表示：式中：c11至c66这36个常数被称为弹性常数。随着各种测量材料应力方法不断出现，这种传统的描述应力-应变关系的线性弹性系数已不能满足现在的科学研究，在用衍射法测量材料应力的研究中，晶面衍射弹性常数的概念随之被提出。用衍射法如X射线衍射，测量材料应力时，通过对满足布拉格衍射条件出现的晶面衍射信息分析，得出该晶面间距的变化，从而求解出该晶面法线方向的应变，将得到的应变与该晶面指数相关的晶面衍射弹性常数相乘即可得到材料的应力[5]。目前关于晶面衍射弹性常数的研究中，较成熟的模型有应变一定的Voigt模型[6]，应力一定的Reuss模型[7]以及考虑材料之间相互作用的 Kroner模型[2]。林政等[8]通过将材料的宏观性能和微观相互作用机理联系在一起，综合分析，结合细观力学[9]的相关知识，从理论上得到了研究单相多晶体晶面衍射弹性常数的计算模型。这些计算晶面衍射弹性常数的模型虽然考虑了材料的夹杂相，但在计算过程中依然把夹杂相和基体相看成一个整体，相当于还是将材料看成单相材料来处理。用研究单相多晶体晶面衍射弹性常数模型去研究复合材料以及多相材料的晶面衍射弹性常数，忽略不同相之间的相互作用，这与实际情况相差过大，需要建立更科学严谨的计算多相多晶体材料晶面衍射弹性常数的理论模型。因此，本文作者将研究对象镍基高温合金看做是基体相γ相(Ni相)和γ′相(Ni3Al相)的两相复合材料，已知Ni单晶体和Ni3Al单晶体均属于立方晶系，建立计算立方与立方夹杂复合材料晶面衍射弹性常数的理论模型。

1.2 模型构建

1.2.1 复合材料相关的宏观弹性常数

运用自洽理论结合 Eshebly等效夹杂模型得到复相材料相关的宏观弹性常数。Eshebly等效夹杂是将复合材料看作是基体相中含有夹杂相的均质材料，假设形状相似并且取向相同的椭球形夹杂相在基体相中均匀分布。Eshebly等效夹杂模型如图1所示。Eshebly等效夹杂模型基本思想是假设在基体相 D中有一个与基体相弹性常数不同且具有本征应变的椭球夹杂相Ω，可用和基体相D相同的弹性常数、与Ω相同形状且本征应变不同的等效特征应变来代替。

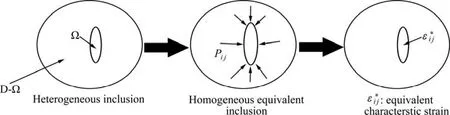
图1 Eshebly等效夹杂模型Fig.1 Eshebly equivalent inclusion model

自洽理论[10-12]的中心思想为在计算夹杂相内部的应力分布时，为了考虑其他夹杂相的影响，认为夹杂相单独处于一有效介质中，而夹杂相周围有效介质的弹性常数就是复合材料的弹性常数。定义ε1为复相材料中夹杂相的平均应变，C1为夹杂相的弹性刚度系数矩阵，为复相材料的平均应变，C为复相材料基体的弹性刚度系数矩阵，A为应变集中因子张量，复相材料外加载荷为σ，则根据Eshebly等效夹杂以及自洽方法有：

对于椭球形夹杂相，夹杂相内部的应变和应力场是均匀的，复合材料在宏观上表现为各相同性，夹杂相在基体相中均匀分布。则有：

式(4)～(7)中：S为复合材料的Eshebly张量；K1和G1分别为夹杂相的体积模量和剪切模量；K和G分别为复合材料的平均体积模量和平均剪切模量。将应变集中因子 A的表达式(7)代入夹杂相平均柔度张量μ1的表达式(6)中，得到夹杂相平均柔度张量μ1与K、G的关系式：

式(9)、(10)中：C为复合材料中夹杂相的体积分数。至此，Eshebly等效夹杂模型结合自恰理论推导已得到复合材料宏观弹性常数平均体积模量和剪切模量的表达式。

1.2.2 晶面衍射弹性常数

复合材料宏观应力应变示意图如下：

图2 复合材料宏观应力分析图Fig.2 Diagram of the macroscopic stress analysis of composite materials

根据图2所示，材料宏观各相同性，受单轴拉伸时，在L3方向的宏观应变φψε为：

式中：l，m和n为L3方向关于坐标系的方向余弦。进一步地，方向余弦为：

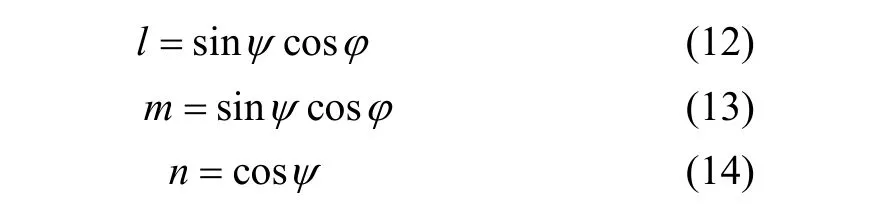
结合应力-应变的线性关系式，得到复合材料相晶面衍射弹性常数的表达式：

式中：υhkl和Ehkl分别为复合材料相(hkl)晶面的衍射弹性模量和泊松比。为了考虑复合材料中的第二相，需要分析复合材料中两相之间的相互作用，即分析材料的微观应力-应变关系。这里的前提是基体材料中含有椭球形第二相夹杂，宏观上表现为各相同性，复合材料在弹性范围内，因为基体相和夹杂相(后称为M相)的弹性常数不同会带来应变附加项ε0，即M相的应变场为(以下公式中有上标“M”的符号均为 M 相单晶体的参量，不加上标的为复合材料参量)：

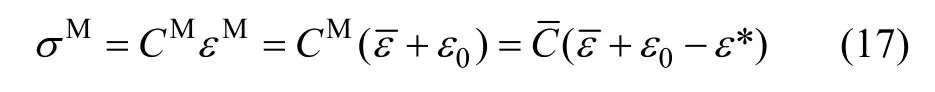
式中：CM为M相单晶体弹性常数；为复合材料的平均弹性常数；ε*为复合材料的固有应变。

根据Eshebly等效夹杂理论有：

即：

式(18)中：SE为Eshebly张量。

又有复合材料负载应变与负载应力关系为：

至此，通过分析复合材料微观应力应变关系，考虑不同相的相互作用，得到TM的表达式。TM类似于材料的弹性柔度张量，给定M相的弹性常数CM，即可得到M相的弹性柔度张量TM。

综上，得到复合材料夹杂相与外加应力的关系为：

夹杂相在基体相中相对均匀分布，当材料仅受单轴拉伸载荷作用时，对夹杂相(h, k, l)晶面上的应变取平均值，再将其与宏观应力-应变关系比对，即可得到立方晶系复合材料晶面衍射弹性常数的表达式如下：

式(24)、(25)中：E与υ分别为复合材料的平均弹性常数和泊松比；是TM对应矩阵i行j列的元素；Г为与晶面有关的参数。

至此，已经建立立方晶系复合材料晶面衍射弹性常数模型，类似地，可以得到其他晶系的晶面衍射弹性常数模型，夹杂相换成基体相就可得到基体相晶面衍射弹性常数，这里不一一赘述。给定相关相在室温的弹性常数 C就可计算室温下相的晶面衍射弹性常数。要计算不同温度下的晶面衍射弹性常数，需要给出不同温度下相的弹性刚度系数C，下面建立计算不同温度下弹性刚度系数C的理论模型。

2 材料的弹性刚度系数矩阵

2.1 能量计算和弹性刚度系数计算

基于准谐德拜模型和第一性原理，计算不同温度下材料的刚度系数矩阵。利用第一性原理计算软件Materials Studio软件包中的Castep模块[13]来计算电子结构。关于Ni3Al金属间化合物的计算，粒子间的相互作用用缀加投影波来表示，交换相关能用广义梯度近似GGA和(PW91)函数来表示，采用15×15×15的K点对布里渊区进行采样，平面波函数的截断能选择460 eV，保证计算过程中达到收敛的要求。对于 Ni的计算，采用广义梯度近似GGA和PBE函数表示交换相关能，利用15×15×15的K点对布里渊区进行采样，平面波函数的截断能选择600 eV，以保证计算过程中达到收敛的要求。计算Ni时考虑自旋极化。

2.2 热力学参数计算

固相热力学性质可用准谐近似的研究方法描述。借助于准谐德拜模型和第一性原理计算，可得到单晶体在不同温度下的平衡体积。

准谐德拜模型计算方程如下：

式中：右边第1项E(V)为体系静态的总能量；第2项中的P和V分别为压强和体积；第3项Fvib(V;T)为晶格振动自由能；第4项Fel(V,T)为电子自由能(影响较小，可忽略)。由上式可知吉布斯自由能与压强、体积及温度有关。

准谐德拜模型中，把Fvib(V;T)[14-15]表示为：

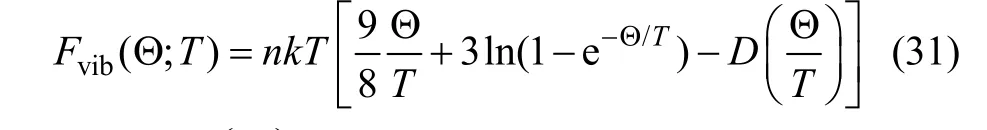
式中：Θ是德拜温度；n为每个原胞中的原子数；k为波尔兹曼常数。德拜温度Θ可表示为：

式中：M为相对分子质量；Bs[3]为绝热体积模量；σ为泊松比；f(σ)和Bs分别用以下的式(35)和式(36)表示[16-17]：

求解非平衡吉布斯函数G*(P,V,T)对体积的最小值，即：

已得到材料在不同温度下的平衡体积，然后得出不同温度下材料的弹性刚度系数矩阵。

3 计算结果与分析

讨论Inconel 718合金的晶面衍射弹性常数，将其视作 80%Ni相(γ相)和 20% Ni3Al相(γ′相)的两相合金，分别取一系列不同的晶格常数值，计算能量和体积，拟合得到Ni3Al和Ni的E-V曲线图(图3和图4)，根据Birch-Murnaghan EOS[14]拟合，得到在0 K零压下Ni和Ni3Al的体积V0，列于表1。

图3 Ni3Al总能量与体积的关系图Fig.3 Total energy of Ni3Al as a function of volume

图4 Ni总能量与体积的关系图Fig.4 Total energy of Ni as a function of volume

表1 Ni与Ni3Al平衡体积的计算值与文献值Table 1 Calculation value and literature value of equilibrium volume of Ni and Ni3Al 10-3 nm3

从表 1看出，本文计算的平衡体积和文献[18]报道的实验测量值很接近，说明本文的计算结果可信。在此基础上，根据准谐德拜模型进一步得到不同温度下的Ni相和Ni3Al相的平衡体积，进而得到在不同温度下这两相的弹性刚度系数矩阵，立方晶系独立的弹性刚度系数为C11,C12,C44。图5和6所示分别为本文作者计算的Ni3Al相和Ni相在部分温度范围内的弹性刚度系数与文献[19-20]报道的实验测量值。从图中可见，不同温度下Ni3Al相和Ni相的弹性刚度系数理论计算值与实验测量值之间的偏差均在误差允许范围内，表明计算结果可靠。将得到的弹性刚度系数代入晶面衍射弹性常数模型中，即可得到不同温度下的晶体衍射弹性常数(弹性模量Ehkl与泊松比υ)，将其与文献[21]报道的实验测量值(550 ℃下)进行对比，如表2所列。

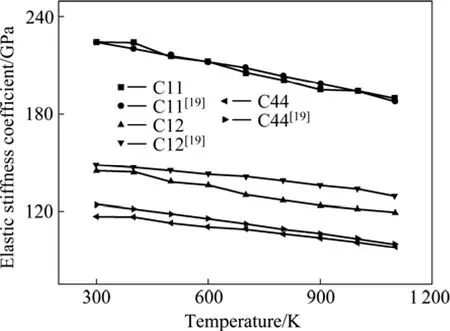
图5 Ni3Al单晶体弹性刚度系数计算值与实验值[19]的对比Fig.5 Comparison between calculated and experimental values[19] of elastic stiffness coefficient of Ni3Al single crystal

图6 Ni单晶体弹性刚度系数计算值与实验值[20]的对比Fig.6 Comparison between calculated and experimental values[20] of elastic stiffness coefficient of Ni single crystal

从表 2可见，本文通过模型计算得到的 Inconel 718合金的γ相晶面衍射弹性常数与文献[15]报道的实验测量值进行对比，其中只有{200}晶面的计算值与实验值偏差稍大，{311}晶面的泊松比υ在室温下的计算值与实验值偏差稍大，其它晶面不同温度下偏差均不超过10%，部分偏差更是在5%以内，总体偏差较小。存在偏差的原因，一方面是本身实验测量时某些晶面存在一定误，另一方面，理论模型是以椭球形等效夹杂为研究前提，而研究对象Inconel 718合金是两相材料，夹杂相并不一定是理想的等效夹杂，且除了γ、γ′两相外还有少量其他相(这里忽略不计)，此外，两相的体积分数也不一定是完全准确比例，不同温度下弹性刚度系数矩阵的计算也存在一定偏差。综合考虑，计算值与实验值有一定的偏差合乎情理。

表2 不同温度下镍基高温合金晶面衍射弹性常数(弹性模量Ehkl与泊松比υ)的计算值与实验值[21]Table 2 The calculated and experimental[21] values of the diffraction elastic constants (elastic modulus Ehkl and poisson

4 结论

用Eshebly等效夹杂理论和自洽方法构建计算立方与立方两相材料晶面衍射弹性常数模型，并基于第一性原理和准谐德拜模型得到材料在不同温度下的晶面衍射弹性常数，计算出Inconel 718合金的γ相在不同温度下晶面衍射弹性常数。计算值和文献报道的实验测量值之间的偏差不超过10%，总体上验证了理论模型的可行性和准确性。