大跨拱桥拱肋拼装温差效应分析及控制方法
2020-05-14刘宇飞李传习于孟生王华王龙林
刘宇飞,李传习,于孟生,王华,王龙林
(1. 长沙理工大学 土木工程学院,湖南 长沙 410114;2. 广西大学 土木建筑工程学院,广西 南宁 530004;3. 广西交通科学研究院有限公司,广西 南宁 530007)
大跨度钢管混凝土拱桥的架设大多采用缆索吊装斜拉扣挂法,其施工控制分为2个阶段:①空钢管成拱阶段;②成桥阶段。空钢管成拱后拱肋线形和内力的调整幅度小,可调手段也不多,因此,空钢管成拱状态是施工控制的关键工况[1]。彭文立[2]等人就缆索吊装钢管拱的施工方法,以某工程为例,讨论了钢管拱在吊装阶段中温度对安装精度和应力测试结果的影响。谢肖礼[3]等人在分析温度效应时,考虑二阶效应,导出了预抬高量与扣索变形之间的关系;以广西邕宁县邕江大桥为例,采用多个温差段,分析了温度对预抬高量的影响。周建庭[4]等人采用多个温差段,分析了温度对吊装扣挂预抬高量和合龙后主拱圈线形的影响规律。温度是施工控制中最为常见与不可控的参数,在钢管拱肋吊装的过程中,温度变化会导致扣点的下沉或上升,影响到拱肋的线形。钢管混凝土拱桥的跨度越大,扣索越长,采用缆索吊装斜拉扣挂方法时温度对拱肋线形的影响越大。因此,研究大跨径钢管混凝土拱桥拱肋吊装阶段消除温度影响的方法与处置措施非常有必要[5]。作者以平南三桥为工程背景,根据悬拼扣挂体系的几何关系,拟分析温度变化在拱肋吊装阶段对标高的影响,并利用Midas/Civil,建立空间有限元模型,分析主拱圈节段吊装过程中温度变化对主拱圈线形的影响,提出在拱肋吊装阶段消除温度对标高影响的施工控制方法,计算出设计温度下平南三桥拱肋的就位标高及不同温度下的位移修正量和索力修正量,以期为类似拱肋吊装过程中的线形控制提供依据。
1 温度变化产生的位移分析
1.1 工程简介
平南三桥上部结构采用中承式钢管混凝土拱桥。主孔跨径为575 m,净跨径为548 m,计算矢跨比为1/4.0,拱轴系数为1.50。拱顶截面径向高为8.5 m;拱脚截面径向高为17.0 m,肋宽为4.2 m;每肋为上、下各2根Φ1 400 mm钢管混凝土弦管,管内混凝土采用C70。主拱肋通过横联钢管Φ 850和竖向2根腹杆Φ700钢管连接主管而构成矩形截面。吊杆间距为15.5 m。主拱主管采用Q420qD 钢材,其余为Q345C钢材。立面布置图如图1所示。

图1 立面布置(单位:cm)Fig. 1 Elevation plan(unit: cm)
单侧主拱肋分为 22个节段,以桥梁中心线对称布置,两岸以跨径中心对称,全桥共计 44个节段。拱肋中距30.1 m,主管通过横联钢管Φ850和竖向两根腹杆Φ700钢管连接而构成。桥面以上主拱上弦平面设置“△”形钢管斜撑,在吊杆处的上、下弦采用“I”钢管竖撑,通过“△”形钢管斜撑与“I”钢管竖撑构成组合式横撑。单根拱肋吊装1#~11#节段的重量分别为:156,164,129,127,215,197,186,181,173,169 和 163 t。
平南三桥采用缆索吊运+斜拉扣挂悬臂拼装工艺施工,单段最大重量为215 t;安装过程中最大悬臂为287.5 m。吊装拱肋的施工顺序为:1A→1B→2B-4B→2A-4A→1-4横联→5A-6A→5B-6B→5-6横联→封铰→7B-8B→7A-8A→7-8横联→9A-10A→9B-10B→9-10横联→11B→B节段合拢→11A→A节段合拢→11横联(其中:数字表示节段号,A表示上游,B表示下游)。
1.2 基本假设
该桥采用智能调载,实时平衡塔顶水平力。通过计算,每升温10 ℃扣索平台最大竖向变位为2.2 cm以内。根据几何关系,计算出塔架竖向变位对拱肋控制点标高的影响[6]。计算结果表明:塔架竖向变位引起的拱肋控制点位移在1.5 mm以内,影响较小。因此,在进行分析和有限元模拟时,塔架与扣索连接处采用固接形式模拟。分析时,假设:①系统升(降)温均匀;②拱肋节段以直代曲;③拱圈各节段之间刚性连接[7-9]。
1.3 温度变化对标高的影响分析
1#节段的施工如图2所示。

图2 1#节段的施工Fig. 2 Construction Section 1#
在1#节段吊装过程中,不考虑温度变化时,1#节段控制点处于A处,扣索长度为L,主拱圈长度为S。当温度变化t ℃时,主拱圈弧长增加ΔS变为S1,扣索长度由L变为L1,控制点由A位移到B处,控制点竖向位移的变化量为;同时,扣索由于温度变化,会有一个伸长量。此时,扣索长度变为L2,弧长为S1不变,控制点由B位移到C处,控制点竖向位移的变化量为。则 1#节段控制点 A竖向位移的变化量为:

2#节段的施工如图3所示。

图3 2#节段的施工Fig. 3 Construction Section 2#
在2#节段吊装过程中,把1#节段当做对2#节段的弹性支承。不考虑温度变化时,2#节段控制点处于A2,扣索长度为L。当温度变化t ℃时,1#节段对2#节段的支撑点O1位移至O2,竖向位移量为上一段分析的Δh1,2#节段扣索长度由L变为L1。此时,控制点A2位移至B2处,控制点竖向位移的变化量为Δh12。当温度变化t ℃时,主拱圈弧长增加ΔS2变为 S1,扣索长度由 L1变为 L2,控制点由 B2位移到C2处,控制点竖向位移变化量为;同时,2#段扣索由于温度变化有一个伸长量。此时,扣索长度变为L3,弧长为S1不变,控制点由C2位移到D2处,控制点竖向位移的变化量为h2L。则2#节段控制点A2的竖向位移的变化量为:

温度变化对后续节段标高的影响可表示为(i=1,2,…,n为当前吊装节段):

式中:Δhi-1i为温度变化 t ℃时,(i-1)#节段控制点竖向位移变化对当前i#节段控制点造成的竖向位移的变化量;为温度变化t ℃时,当前节段扣索伸长引起的当前i#节段控制点竖向位移的变化量;为温度变化t ℃时,当前i#节段拱圈弧长的变化量所引起的竖向位移的变化量。
以 1#节段为例,计算。拱肋和扣索的伸长分析分别如图4,5所示。

图4 拱肋伸长分析Fig. 4 Analysis of arch rib elongation
设塔顶 D到拱铰 O之间连线长度为 P,由ΔDEO可得:

式中:M为塔轴线桩号与拱铰桩号之差;N为塔架索鞍处与拱铰的高程差。
当温度变化t ℃时,计算拱肋伸长量ΔS。由于变化量相较整个结构比较小,因此,假设拱圈伸长变化量不造成索长的伸长(索力不变),即吊点由 A变到C时索长仍为L。此时,拱肋长度为:

式中:k拱为拱肋的线膨胀系数;t为温度的变化量。
M,N,P,S,S1和 L已知时,由三角形关系求得 α和β,计算出温度变化前吊点与拱铰的高程差y1和变化后吊点与拱铰的高程差y2,则温度变化t ℃时拱肋伸长量所造成标高的变化值为:


图5 扣索伸长分析Fig. 5 Elongation analysis of a buckle
当温度变化t ℃时,经由拱肋伸长,扣索伸长,吊点C位移至点F,扣索的伸长量为ΔL。扣索伸长后的长度为:

式中:k索为扣索线膨胀系数。
由已知量求得α和β,计算出经由拱肋伸长后扣索由于温度变化伸长而产生的竖向位移变化量,最终算出竖向总位移Δh1。

式中:y1,y2和y3分别为控制点初始标高、温度变化时只考虑拱肋弧长变化后的控制点标高及温度变化后控制点的标高;α,β和γ分别为拱肋与地面线的初始夹角、温度变化时只考虑拱肋弧长变化后的拱肋与地面线的夹角及温度变化后的拱肋与地面线夹角。
将式(9)代入式(3),即可求得下一节段竖向位移的变化量。
2 消除拱肋吊装节段温度变化影响的方法
1) 确定拱肋的合拢温度,即作为扣索和拱肋节段的基准温度。通过基准温度计算出各阶段控制位移(将裸拱自重作用下的位移作为控制位移)。
2) 当施工i#节段时,通过求得的i#节段施工完成时的线形如图 6所示(虚线为基准温度线形)。同时,将1#~i#拱肋节段和对应扣索由基准温度升高到i#节段施工时的温度,从而得到当前施工阶段温度下的线形,作为当i#节段的施工控制线形(图6中的绿实线)。在 i#节段吊装温度与前(i-1)#节段吊装温度不同的情况下进行拼装与 1#~i#节段均在同一温度(当前施工阶段温度)下吊装的线形一致,即达到各节段间无温度差拼装的效果。如:基准温度为25℃,施工1#节段时温度为35 ℃,施工2#节段时为40 ℃,则可将1#节段的温度变化量10 ℃代入式(9)计算出1#节段控制位移的温度修正量,施工1#节段。施工2#节段时,温度变化量为15 ℃。根据式(9)计算出当前节段温度产生的总竖向位移,再根据式(3)计算出 2#节段控制的温度修正量,并以此来 施工。

图6 i#节段施工时的控制线形Fig. 6 Control alignment during the construction of Section i#
3) 每个节段均按上一步的方式施工,就可以得到合拢前施工阶段温度下的拱肋线形(图 7中绿实线)。当温度变化到此施工阶段时,该线形与按基准温度施工下的线形一致。因此,等到环境温度与基准温度一致时,则线形将回到基准温度下的线形,此时,就可以合拢。
该方法能确保所有节段在不同温度下施工按预期的线形合拢。

图7 合拢前施工阶段温度下的拱肋线形Fig. 7 Arch rib alignment at temperature during the construction before closing
3 吊装节段温度修正量的分析
3.1 模型的建立
本研究采用Midas Civil 2018软件,计算扣索力、控制位移及温度变化时位移的修正量。因此,未建立塔架模型,且扣索只模拟拱肋扣点至塔架索鞍段。由于扣索为通索,因此按长度比可换算出相应扣索的弹性模量和线膨胀系数。因施工时为南、北岸同时对称施工,故只分析模型 1/2的拱圈(南岸)。有限元模型如图8所示。

图8 拱肋拼装有限元模型Fig. 8 Assembled finite element model of an arch rib
采用桁架单元模拟扣索,梁单元模拟拱肋,板单元模拟拱脚处加劲板。该模型共1 724个节点,桁架单元72个,梁单元3 158个,板单元56个。
由于在模型中扣索长度比实际长度短,为了保证扣点位移的变化量Δl与实际的一致,对扣索的弹性模量E进行了换算。

式中:F为扣索力;L为扣索长度;A为钢纹丝面积。
在相同的扣索力和钢索丝面积情况下,当减小扣索长度L时,需要等比例地减小扣索的弹性模量E,从而满足扣点位移的变化量Δl不变。同理,对扣索线的膨胀系数k也进行了换算。

式中:Lt为温度变化t℃时的索长;L0为基准温度下的索长。
钢材基本容许重量取 83.22 kN/m3,是考虑了1.06的重力增大系数。该系数用于模型中未考虑的节点板和焊缝等荷载。
3.2 考虑温度变化的位移修正量
假设拱肋合拢温度为 25 ℃,即作为扣索和节段的基准温度,计算升温10 ℃即升至35 ℃时的位移变化量。施工时,由于 1#~4#节段没装横撑,因此上、下游1#~4#节段互不影响,模型中1#~4#节段统一升温。根据温度控制方法,考虑i#节段施工后整体温度变化对i-1控制点的影响与(i-1)#节段施工时温度变化对i-1控制点的影响可能不同,着重考虑竖向位移的变化量,对封铰前上游控制点(2A,3A和4A)和封铰后上游控制点(7A,8A和9A)的竖向位移进行了分析,见表1。
对封铰前下游控制点(2B,3B和4B)和封铰后下游控制点(7B,8B和9B)的竖向位移也进行了分析,见表2。

表1 升温10 ℃上游典型控制点的竖向位移Table 1 Vertical displacement of typical upstream control points with the temperature rises by 10 ℃

表2 升温10 ℃下游典型控制点的竖向位移Table 2 Vertical displacement of downstream typical control points when the temperature rises by 10 ℃
从表 1,2中可以看出,除了 6#,7#和 11#节段,施工i#节段在整体升温后该节段控制点的位移变化量与(i+1)#节段后整体升温控制点的位移变化量差距很小,可以忽略。安装6#节段后整体升温时,1#~6#节段控制点位移差距较大,造成该现象的原因是:6#节段施工完成后进行了封铰,边界条件由铰接变为固接的悬臂结构。同理,11#节段施工完成后各个控制点位温度的位移变化量与前一节段对比差距较大的原因是:11#B节段施工完成后进行临时合拢。在有边界条件变化的施工节段,需等到温度变为合拢温度时才进行施工,这样可以保证每个控制点的温度最终为合拢时的温度。在控制位移处,即消除温度在拱肋吊装节段对线形的影响。若 6#,7#节段变化较大,就需要在6#节段施工完毕后等到最终合拢温度时进行封铰。
经计算分析可知,标高随温度的变化量呈线性关系。计算得到的 10 ℃温度变化下各节段控制位移修正量见表 3。其他温度的修正量只需要通过计算结果等比例变化便可以得到。
3.3 考虑温度变化的索力修正量
分别计算1#~4#节段温度升高5,10和15 ℃时索力的变化量。4#扣索索力的变化量[10-11]见表4。
从表4中可以看出,索力随温度的变化呈线性变化。根据升温前、后索力的变化量,可计算出各个施工阶段变化 10 ℃时的索力修正量。其他温度下的索力修正量可由表5数值等比例变换得到。

表3 各节段控制位移修正量Table 3 Control displacement correction of each segment
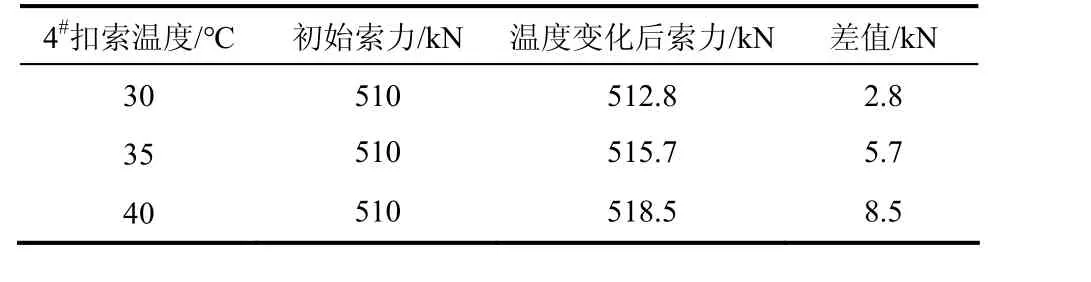
表4 升温索力的变化量Table 4 The change of cable force at overhand temperature

表5 扣索力修正量Table 5 The cable force correction
4 结语
以平南三桥为工程背景,分析了温度变化对拱肋位移控制点的影响,计算了拱肋控制位移,研究了大跨径中承式钢管洪凝土拱桥在拱肋吊装节阶段如何消除温度变化对拱圈线形的影响,并提出了拱肋吊装阶段进行温度控制的方法。得到的结论为:
1) 大跨径钢管混凝土拱桥拱肋吊装阶段需考虑温度变化对拱圈线形的影响。
2) 提出了控制拱肋吊装阶段温度影响方法。通过有限元模拟,验证了该方法是可行的,可为同类型的桥梁施工控制提供依据。
3) 使用本研究提出的方法时,需在有边界条件改变的施工阶段等待温度达到设计合拢温度后再进行下一节段的施工。
