带时间窗车辆路径规划算法研究与实现
2020-05-14孙沪增李章维秦子豪周晓根张贵军
孙沪增,李章维,秦子豪,周晓根,张贵军
1(浙江工业大学 信息工程学院,杭州 310023)
2(美国密歇根大学安娜堡分校 计算医学与生物信息学系,美国 密歇根州 48109)
E-mail:zgj@zjut.edu.cn
1 引 言
随着互联网技术的迅速发展,传统物流配送产业的优化转型已迫在眉睫.车辆路径问题作为物流配送产业研究的热点问题之一,对物流产业的转型升级有着指导意义.考虑时间窗因素的车辆路径问题(VRPTW),更加符合实际配送问题需求.因此,VRPTW问题得到国内外学术和产业界的广泛关注[1].
VRPTW是一个NP-hard组合优化问题,传统的精确算法只能解决规模相对较小的问题,且耗时较长,而现实物流配送往往涉及大规模的客户群体,因此元启发式算法由于其较好的收敛性往往成为解决此类问题的首选方案.这也促使了国内外学者对VRPTW问题转向了元启发式算法的研究.Alzaqebah等提出了一种通过限制差解的最大数量来避免人工蜜蜂盲目搜索,从而提高VRPTW收敛速度的优化人工蜂群算法[2];Nalepa等提出了一种能够平衡搜索空间的探索和利用的自适应模拟算法来解决VRPTW问题[3];李珍萍等建立了多需求混合整数规划模型,设计了一种求解模型的联合优化遗传算法,为解决实际问题提供了决策依据[4];李兵飞等设计了一种改进的双重进化人工蜂群算法来求解速度时变VRPTW问题,并通过实例验证了模型和求解方法的有效性[5];Akpinar等提出了一种蚁群系统和大邻域搜索的混合算法,使得在求解过程大大提高了算法的多样性[6];Osaba等提出了一种渐进式离散萤火虫算法,成功将萤火虫算法应用到VRPTW问题的求解[7].
以上VRPTW问题的研究主要针对测试数据集来验证算法的有效性.然而,结合实际路网的算法应用在现有文献中还鲜有报道.本文针对带时间窗的车辆路径问题,设计了一种基于局部增强搜索策略混合的蚁群算法,通过标准数据集的测试验证了算法对不同类型、不同时间窗宽度VRPTW的适用性;进一步基于浙江省杭州市路网数据集,基于ArcGIS平台,设计并开发了一套物流配送系统.
2 带时间窗的车辆路径问题数学模型
假定模型配送中心只有一个,本文考虑如下VRPTW的数学模型[8,9,14,15]:
(1)
(2)
(3)
(4)
(5)
(6)
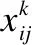
目标函数(1)表示完成所有客户配送成本最小;约束(2)表示每辆车配送的客户需求总数不能大于车的最大装载量;式(5)表示每个客户点有且仅有一辆车为其服务;式(6)表示所有客户点有且仅被配送一次;在上述模型基础上引入如下时间窗约束条件:
(7)
如果违反时间窗约束条件就需要进行惩罚.设客户i的时间窗范围为[ai,bi],Ti为车辆到达客户i的时间,其中:ai为顾客i允许的最早服务时间,bi为顾客i允许的最迟服务时间.e为惩罚系数;半软时间窗约束允许车辆到达i的时间早于ai但不允许晚于bi,早于ai配送客户点i,必须等待至ai再为客户i服务,因此需要支付一定的惩罚费用p(Ti)=e(ai-Ti)2,迟于bi配送的客户点i则通过后续的时间窗约束直接剔除.
3 基于混合局部增强搜索策略的蚁群算法
蚁群算法是一种模拟大自然蚂蚁群体觅食行为的模拟优化算法.通过蚂蚁间信息素交互的正反馈机制,蚁群算法往往能较快地收敛于最优解;但也是由于这种正反馈作用力,算法往往容易陷入局部最优解,无法每次都能快速地收敛于全局最优解[10].因此本文在蚁群系统的基础上引入了局部搜索等策略,通过对蚁群算法每代最优解进行局部搜索指导,提高了算法的全局搜索能力与收敛速度,进而能够避免算法早熟、停滞.
3.1 改进的蚁群算法
1)路径构造过程
本文采用的路径构造方式与传统的VRP问题路径构造方式有所不同.通常的构造方式,每只蚂蚁产生的子回路仅是一个可行解的一部分,获得一个完整的可行解需要各蚂蚁产生的子回路组合来生成一些可行解,当然也可能没有可行解;这种路径构造方式生成的可行解往往需要通过对大量的子回路组合产生,在一定程度上影响了算法的效率,也无法很好地保证每次迭代可以出现较好的可行解[11].
而本文改进的路径构造方式为一只蚂蚁即可产生一个可行解,结合多种策略可以保证获得较优的解.每只蚂蚁通过并行的方式随机从各客户结点出发,根据状态转移规则和确定性与随机性选择相结合的选择策略来指导蚂蚁选择下一个需要配送的客户,并实时更新自身的禁忌表用来指导后续路径构造过程[12,16].
(8)
(9)
其中:τij为信息素浓度;ηij=demandj/dij为启发因子,demandj为客户j的货物需求量,dij为客户i,j之间成本;widthj为客户j的时间窗宽度,时间窗越紧,优先配送级别相对较高;waitj为车辆在配送客户j时需要等待的时间,当车辆早于客户j时间窗到达,就需要等待,等待时间越长会影响配送效率、增加配送成本.当车辆在客户j时间窗内到达,在j的等待时间waitj=0,在算法中取一个极小值;savej为从客户i配送到客户j比从客户i回到配送中心,再从配送中心出发到客户j的节约量;allowedk为未配送的客户集合;α,β,γ,θ,ω分别为各影响因素的权重因子;r为[0,1]之间的随机数;r0为[0,1]之间的常数,用来控制转移规则.当r>r0时,算法依概率选择下一个配送的客户点,当r≤r0时,算法根据轮盘赌策略伪随机选择客户点.
2)信息素更新规则
当所有蚂蚁构造完成一次可行解时,算法进行全局信息素更新,根据精英蚂蚁策略[13]更新全局信息素,对于精英蚂蚁额外进行一次信息素累加,这种策略体现了算法的正反馈特性,但经过几代计算后易导致某个较好解路径上的信息素浓度过高,从而陷入局部最优.因此算法引入最大最小信息素策略(MMACA),把信息素浓度限制在[τmin(t),τmax(t)]区间[13]内,并根据每代产生的最优路径来动态更新最大最小信息素,使算法具有较好的自适应性.信息素更新规则[14,17]如下:
τij(t+n)=(1-ρ)*τij(t)+Δτij
(10)
(11)
(12)
(13)
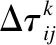
采用全局信息素更新策略来指导蚂蚁的结点选择过程,虽然考虑了信息素的反馈,但仍具有一定的延迟性,不能及时地引导蚁群寻找最优路径.有不少学者结合构造性的贪婪算法来指导局部信息素更新,这样往往能在算法早期获得一个较优解,把该解作为模拟退火算法的初始解,进行全局优化搜索,往往可以获得更优解.算法中结合实际问题利用提前可知的先验知识来指导结点的选择,譬如配送完客户点i之后必须立马配送客户点j,这类先验知识往往可以使算法有较好的运算效率.
3.2 算法描述
为了弥补蚁群算法容易进入局部优解的特点,在算法的不同阶段采用不同的策略,从而扩大搜索空间,获得全局最优解.
3.2.1 局部搜索策略
算法在蚂蚁构造路径的过程中以及迭代出全局较好路径时对解进行局部搜索,从而有概率通过差解或较优解产生全局最优解.算法中充分利用了1-Relocate、2-Relocate、2-opt、2-opt*、Exchange以及Exchange*局部搜索算子对可行解的子回路以及子回路之间进行路径改进优化,分别如图1-图6所示.
1)1-Relocate算子路径改进
算法对同一子路径内的两客户结点进行1-Relocate算子改造,将前一客户结点插入到后一客户结点之后,若改造后的解符合约束条件,且成本比改造前的子路径低则保留改造结果,反之则不保留.
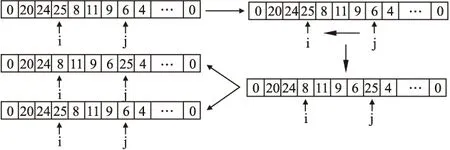
图1 子回路内顶点重定向
2)2-Relocate算子路径改进

图2 子回路间点顶点重定向
算法对不同子路径间的两客户结点进行2-Relocate算子改造,将前一客户结点插入到后一客户结点之后,若改造后的解符合约束条件,且成本比改造前的子路径低则保留改造结果,反之则不保留.
3)2-opt算子路径改进
算法对同一子路径的两客户结点之间的所有结点进行2-opt算子改造,将这些客户结点反向插入原先的队列,若改造后的子回路符合约束条件,且成本比改造前的子路径低则保留改造结果,反之则不保留.
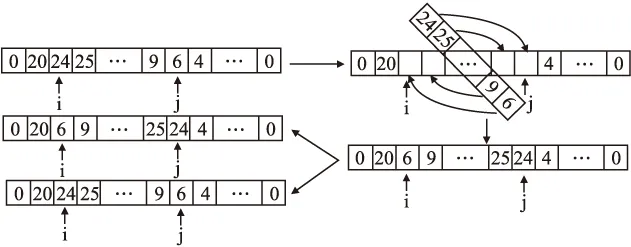
图3 子回路内2-opt
4)2-opt*算子路径改进
算法对不同子路径间的两客户结点之间的所有结点进行2-opt*算子改造,将前一客户结点插入到后一客户结点之后,若改造后的每个子回路都符合约束条件,且总成本比改造前的子路径低则保留改造结果,反之则不保留.
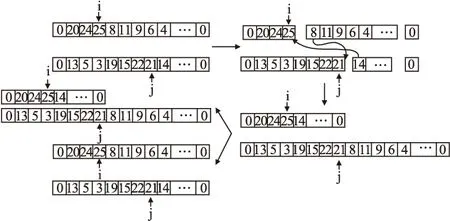
图4 子回路间2-opt*
5)Exchange算子路径改进
算法对同一子路径内的两客户结点进行Exchange算子改造,将两结点互换位置,若改造后的子回路符合约束条件,并且成本比改造前的子路径低则保留改造结果,反之则不保留.
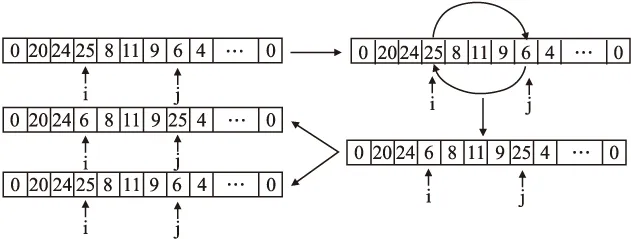
图5 子回路内交换
6)Exchange*算子路径改进
算法对不同子路径间的两客户结点进行Exchange*算子改造,将两结点互换位置,若改造后的都符合约束条件,且总成本比改造前低则保留改造结果,反之则不保留.

图6 子回路间交换
3.2.2 动态更新信息素挥发以及转移规则参数策略
当算法的当前代最优解和前代最优解连续n代的差值小于信息素挥发率ρ更新的临界阈值RHO,则说明算法可能陷入了局部最优.将信息素挥发率ρ逐代增加,直至出现新的全局最优解;若经过2n代计算仍然没有搜索出新的最优解,将信息素挥发率ρ逐代减小,加速算法收敛,最终输出全局最优解.
在算法早期,设置较大的转移规则参数r0,进行确定性搜索,使算法加速收敛到较优解;在算法中期,设置较小的r0,进行探索性搜索,扩大搜索空间,摆脱算法容易陷入局部优解的缺点;在算法后期,设置较大的r0,加快收敛速度,在局部空间搜索最优解,提高算法运算效率.即(NCmax为算法最大迭代次数):
(14)
3.2.3 算法步骤
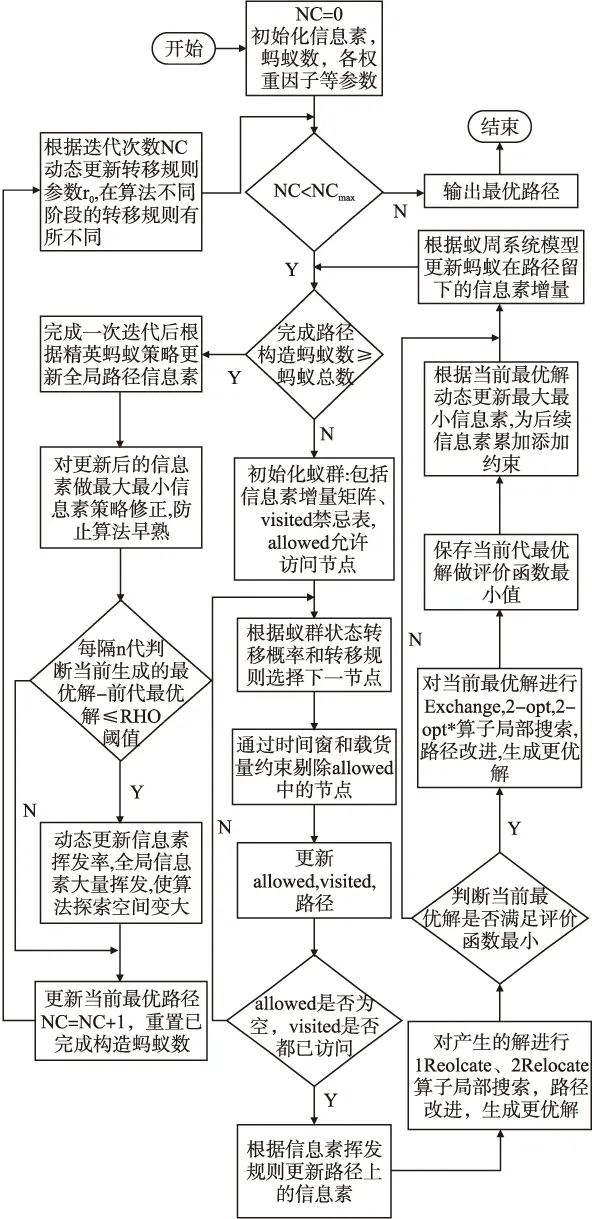
算法步骤及流程图如图7所示:
1)参数初始化:最大迭代次数NCmax、信息素初始浓度τij、最大最小信息素系数C、蚂蚁数K、车辆最大载货量Qk、状态转移概率中的权重因子α,β,γ,θ,ω、信息素挥发率ρ、蚁周系统参数O以及客户点数据等参数.
2)初始化蚁群,令各蚂蚁随机从各客户结点出发.
3)子回路构造:根据状态转移规则和确定性与随机性选择相结合的选择策略公式(8),公式(9)选择下一节点,通过时间窗和载货量约束来逐步增加禁忌表中的客户点.
4)若禁忌表未满,则跳转回步骤(3).
5)若禁忌表已满,得到可行解.对可行解进行局部搜索策略优化解,根据公式(10),公式(11),公式(12)更新挥发后的信息素和蚂蚁分泌的信息素增量.
6)若产生更优解,保存当前最优解,根据公式(13)动态更新信息素最大最小值.
7)完成一次迭代后根据精英蚂蚁策略(11)对全局信息素更新,对全局信息素进行最大最小信息素策略修正,并根据信息素挥发策略动态更新ρ.
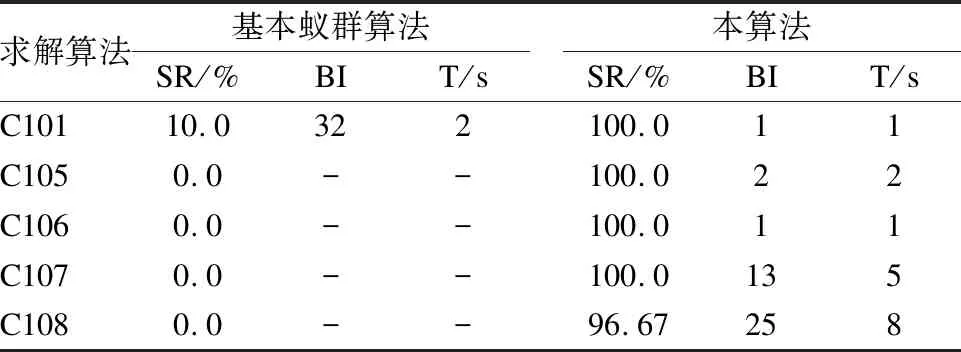
8)NC=NC+1,根据转移规则参数策略动态更新r0,若NC 实验数据集选取Solomon标准测试数据集[15],客户点规模为100.算法使用java语言来实现,实验环境为:Intel(R)Core(TM)i7-6700HQ CPU@2.60 GHz with 8GB RAM,Window10,算法代码运行平台使用IntelliJ IDEA 2017.本文对算法的参数进行大量组合测试用来选择较合理的参数组合,最终选取:α,β,γ,θ,ω,ρ的值为(3.0,4.0,1.0,3.0,2.0,0.8);NCmax设为50代,信息素挥发率ρ为0.8,蚁周系统常系数O为500.0,信息素初始浓度τij为1.0,MMAS系数C为200.0;1-Relocate、2-opt以及Exchange算子一次迭代的优化次数为5次,2-Relocate、2-opt*以及Exchange*算子一次迭代的优化次数为3次.表1是算法程序对部分测试数据集C101、C105、C106、C107、C108(最优解全为828.937)均运行30次的实验结果,其中求出最好解的概率SR,求出最优解时的平均迭代次数BI,平均计算时间T. 图7 算法流程图 为验证引入的策略在迭代过程中对算法探索全局最优解的优化改进,本文列出了算法对C108数据集测试30次产生的平均每代最优解图,如图8所示. 由表1可知,在较短的最大迭代数限制下,基本的蚁群算法基本无法得到全局最优解,而本文改进的蚁群算法几乎都在50代之内收敛到了最优解,并且在运算效率上优于基本蚁群算法,而从图8中分析得出,算法在迭代过程中多次陷入局部最优解,但本文引入的策略可以有效地增强算法全局搜索能力,使算法摆脱局部最优,最终收敛到全局最优. 表1 在50代之内算法数据集测试表 Table 1 Algorithm data set test within 50 generations 求解算法基本蚁群算法SR/%BIT/s本算法SR/%BIT/sC10110.0322100.011C1050.0--100.022C1060.0--100.011C1070.0--100.0135C1080.0--96.67258 图8 测试C108数据集30次每代最优解平均值趋势图 基于上述算法,针对浙江省杭州市实际路网数据,利用ArcGIS平台开发了物流配送管理系统,实现运输任务、运输规划等功能.系统以该地区地理信息数据为基础,通过对数据进行转弯要素、道路等级以及方向要素、网络连通性[6,16]、属性赋值等手段来构建实际路网模型,并通过Dijkstra算法[10,17]得到配送中心和各商场之间的最短距离和最短时间,从而获取最短距离和最短时间的OD成本矩阵;本文以图9为例说明,针对某物流公司日常需要将货物从配送中心运送到25家商场的实际VRPTW问题,图中配送中心和所有商场分布用数字1~25表示,配送中心和商场的货物需求量、时间窗口以及卸货所需时间等信息如表2所示;配送中心和所有商场之间的最短时间OD成本部分数据如表3所示.算法的主要目标是为物流公司生成一组货车车队,车队中的每辆卡车分配一组所要服务的商场,并确定送货的顺序,从而将总配送成本控制在最低. 图9 商场及配送中心分布图 表2 配送中心和25个客户点信息 Table 2 Distribution center and 25 customer information 0~12节点0123456789101112需求量/磅0170615331580128913021775101417611815170910451414开始时间9:0014:5414:209:2513:429:0613:0110:0610:3912:2711:1811:5413:13结束时间17:0015:1514:389:5714:049:2613:3310:2711:0612:5511:3912:1613:40卸货时间/分010813101213810121081213~25节点13141516171819202122232425需求量/磅1863179113731962187210561950136415251767105315931469开始时间9:1212:4011:2912:059:3810:1010:489:0414:5514:1513:449:2510:06结束时间9:3613:0111:4712:259:5710:3911:149:2815:1514:4314:029:5610:27卸货时间/分10118108121310101210128 篇幅有限,表3只给出了其中15个商场与配送中心之间的OD成本矩阵,从上述数据中可以发现实际路径问题中客户点i配送到客户点j的成本与客户点j配送到客户点i是有差别的,这比常规VRP问题中仅仅靠计算各客户点坐标之间的欧式距离作为成本更符合实际情况. 1)无时间窗约束车辆配送问题应用 本案例应用中25家商场散落在城市的四周,货车必须经过复杂的城市路网才能配送下个商场,使用的货车的最大装载量为15000磅;货车司机的费用为每小时75元,货车的燃料消耗、日常维护等费用为每千米6元;由于长期驾驶会导致疲劳驾驶,公司规定一次配送司机驾驶时间不能超过7小时(不包含等待服务时间);算法对于没有时间窗同时符合上述要求的最优配送方案如图10所示.此方案配送一次公司的费用成本约为1866.9元,其中第一辆货车配送路线“1”为:0-21-20-24-25-23-10-22-9-0,货车装载量为12295磅,司机花费约6.77小时完成此次配送;其中第二辆货车配送路线“2”为:0-19-18-17-8-1-2-3-15-0,货车装载量为12831磅,司机花费约6.47小时完成此次配送;其中第三辆货车配送路线“3”为:0-16-13-4-7-6-11-12-5-14-0,货车装载量为13455磅,司机花费约6.15小时完成此次配送. 表3 配送中心和15个客户点之间的最短时间OD成本矩阵(分钟) Table 3 Minimum time OD cost matrix between distribution center and 15 customer(min) 00.0012.5912.278.3011.8110.5217.3213.7217.3716.0420.7216.2710.708.887.674.75112.660.004.364.596.219.8414.549.7516.7426.1130.7816.9511.329.3811.928.44212.434.370.004.582.486.1211.837.7617.0825.1129.7913.237.596.208.748.4338.474.594.570.004.748.2514.1010.0214.0221.9226.5915.499.856.378.134.26411.916.202.484.720.003.869.695.6117.2324.5729.2411.085.453.726.268.58510.199.926.208.013.950.009.786.1820.9421.8526.5310.733.123.383.538.92617.3814.8411.9614.209.799.780.006.8326.7129.0433.727.658.7712.0310.8316.21713.599.757.8110.055.645.996.570.0022.5625.2529.927.914.978.247.0312.42817.5816.3516.6313.6016.8020.4426.1522.070.0031.7336.4127.5521.9119.0019.8514.66916.4225.8324.9821.6424.5222.3929.1925.5932.910.0015.5728.1422.5721.5519.5418.721020.1329.5328.6925.3428.2326.1032.8929.3036.6214.740.0031.8526.2725.2623.2422.431116.3116.6912.9715.2110.8010.577.697.9227.7127.9632.630.009.1812.8211.6115.341210.6611.337.619.855.443.448.805.1122.3522.3227.009.300.004.963.308.79138.929.396.186.393.703.7211.537.9419.3921.5726.2512.494.700.002.635.97147.6011.928.728.066.233.8710.777.1720.2519.5524.2311.733.302.630.005.85155.038.348.364.068.539.1216.0212.4315.1218.6723.3415.888.725.915.800.000123456789101112131415 图10 无时间窗配送方案 2)带时间窗约束车辆配送问题应用 然而实际VRP问题一般都带有时间窗约束,在算法中加入表2的各商场的时间窗约束后求出的最优配送方案如图11所示.此方案配送一次公司的费用成本约为2106.1元,其中第一辆货车配送路线“1”为:0-20-24-25-10-9-23-22-21-0,货车装载量为12295磅,司机花费约6.55小时完成此次配送,由于提前到达商场而等待商场开始服务的等待时间约为1.38小时;第二辆货车配送路线“2”为:0-13-3-8-15-16-14-12-0,货车装载量为11744磅,司机花费约4.87小时完成此次配送,由于提前到达商场而等待商场开始服务的等待时间约为0.45小时;第三辆货车配送路线“3”为:0-5-7-11-6-4-2-1-0,货车装载量为9664磅,司机花费约6.53小时完成此次配送,由于提前到达商场而等待商场开始服务的等待时间约为2.13小时;第四辆货车配送路线“4”为:0-17-18-19-0,货车装载量为4878磅,司机花费约2.41小时完成此次配送,由于提前到达商场而等待商场开始服务的等待时间约为0.6小时. 图11 带时间窗配送方案 从上述两种配送方案中进行分析,车辆总数从3辆车变成了4辆,且原先较早配送的节点可能由于时间窗约束变成较迟配送的节点,譬如0号配送中心到21号商场的时间比0号配送中心到20号商场要短,但由于21号商场要求货物配送服务的时间窗为[14:55,15:15],20号商场的时间窗为[9:04,9:28],所以导致20号商场优于21号商场先进行配送服务,同时由于0号配送中心的统一发车时间为上午9点,那么20号商场的货物配送服务是非常紧急的,因此其中一辆货车优先去20号商场进行配送服务;而车辆从3辆增加到4辆的主要原因是由于部分商场的时间窗比较相近,一辆车无法在时间窗约束下满足这些商场的需求,因此必须派出不同的车辆分别进行配送,譬如17号商场的要求服务时间和3号商场是十分相近的,但由于第二辆货车在选择对3号商场进行配送任务后是无法赶到17号商场进行令商场满意的配送服务,因此物流公司需要增派一辆货车对这些时间窗与其他车辆配送的商场节点相近的商场进行令客户满意的配送服务. 本文对带时间窗的车辆路径问题进行研究,在传统数学模型的基础上设计了一种基于蚁群系统和局部增强搜索策略的蚁群算法,针对蚁群算法搜索空间小、容易陷入局部最优的特点,加入了多种局部搜索算子来改进算法全局探索的能力,同时引入了动态更新信息素挥发以及转移规则参数策略,来使算法在运行的不同阶段动态进行自适应参数选择,进而通过与标准测试数据集比对表明算法在较短时间内得出满意解,最后将算法应用到实际案例中,验证了算法在解决具有较大规模的实际车辆路径问题的有效性.4 实验结果与分析
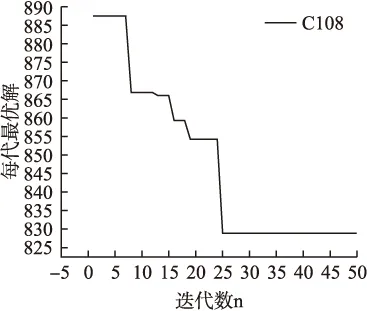
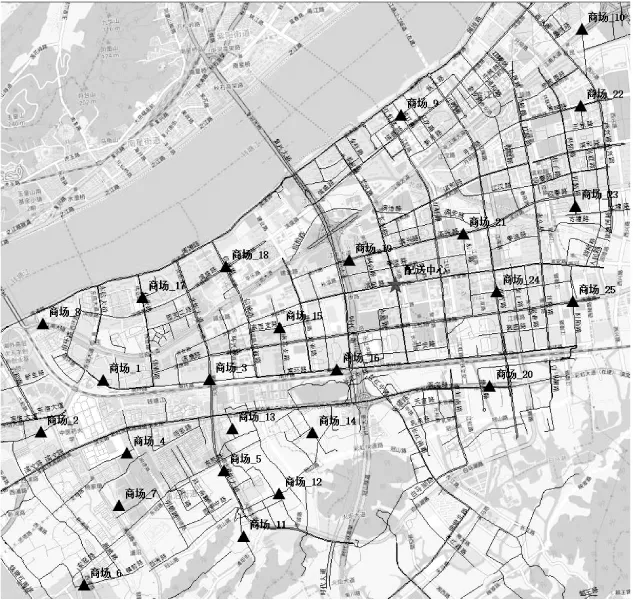
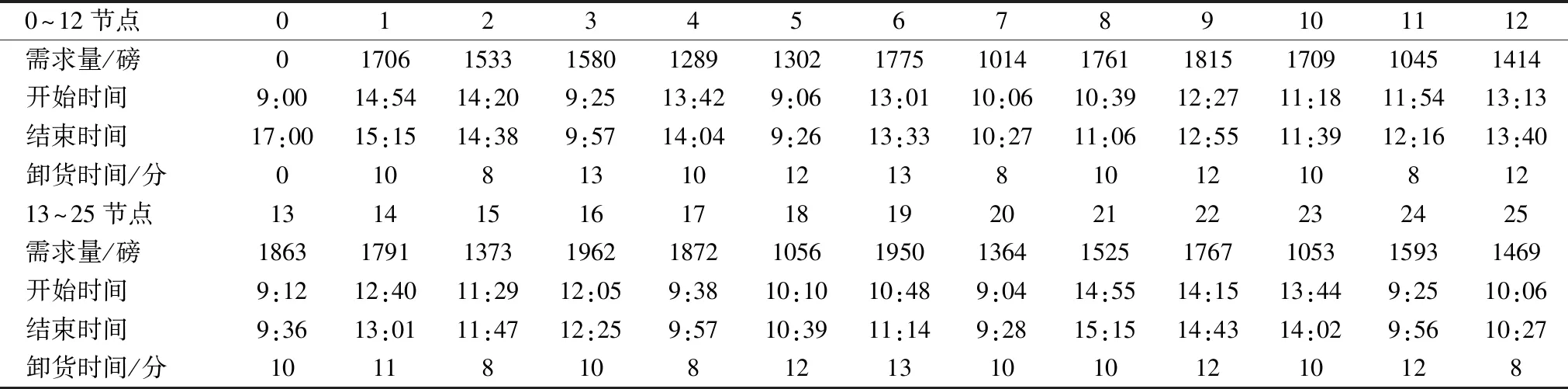
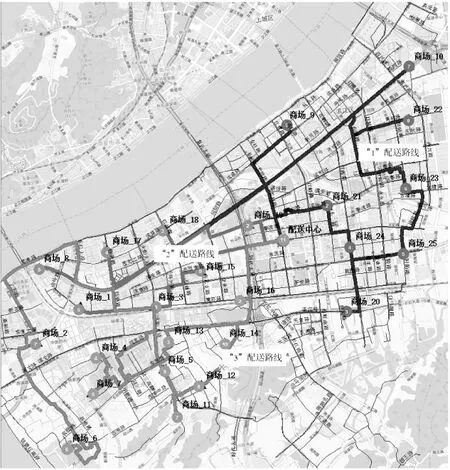
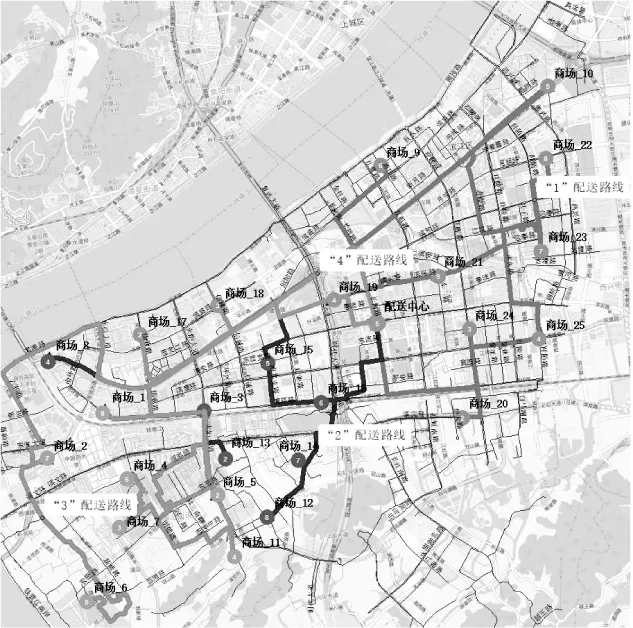
5 案例应用

6 结 论
