基于张量分解的多维信息融合兴趣点推荐算法

杨晓蕾，李 胜，何熊熊，刘桂云

(浙江工业大学 信息工程学院， 杭州 310023)

E-mail:alleny_29@qq.com

1 引 言

近些年来，通信网络发展飞速，移动设备随之普及，网络社交平台受到大众青睐，人们可以方便地在例如微博，Foursquare， Instagram等平台上交友互动，与大家分享有趣的经历，这一类平台统称为基于地理位置的社交网络(Location Based social networks，LBSN).用户访问自己感兴趣的兴趣点(Point-of-Interest，POI如：影院，健身房等)，并通过移动设备定位发布在网络上，从而产生了大量的用户签到信息.这些签到信息中包含了许多具有挖掘价值的内容，如：签到时间、地点经纬度、POI类别等.利用这些数据做个性化POI推荐的系统应运而生，此类系统不仅可以为用户省去繁复查询的时间，还可以帮助商家完善已有兴趣点的服务或发掘新的兴趣点进行商铺选址[1]，进而带来更好的经济效益.尽管个性化POI推荐系统能带来许多便利和商机，但它也面临着许多挑战.

首先，由于POI地点的数量巨大，用户的签到信息中包含的地点数量远远少于POI总数，特别是有一些POI地点尚未被人们发掘，因此签到数据十分稀疏[2]，这将导致度量相似性时出现较大的误差，影响推荐准确率.其次，用户的签到信息只展示了用户去过一些POI这一现实情况，但并没有直接给出用户对访问过的POI的偏好.由于签到信息只提供隐式反馈的性质，从用户角度来看，推荐系统需要分析用户的签到频率和影响因素，利用用户相似性预测用户的偏好，推送符合偏好的兴趣点；从兴趣点方面出发，系统利用地理-社会-评论关系构造POI相关度矩阵并聚类，得到具有兴趣点本身代表性的推荐列表[3].

值得注意的是，一个人决定出行的过程是非常复杂的，受到很多因素影响，主要包括：

1)地理因素，Li等人[4]分析签到信息发现，POI的访问频率通常与用户离“常驻地”的距离成幂律分布，人们在考虑交通便利程度和路程远近的因素后，往往会选择离居住地较近的POI.

2)社会因素，文献[5]中提到朋友之间会有相似的兴趣爱好，并且朋友对POI美好的描述使得这些POI更具有吸引力，人们更倾向于选择朋友分享过的POI.

3)时间因素，文献[6，7]中研究发现，人们的出行规律与时间相关，他们会在特定的时间段去到特定的地点，比如，中午的时候，人们会去餐厅，在晚上大家则会选择酒吧之类的地点.

4)类别因素，Chen等人[8]提出POI类别对人们的选择颇有影响.不同的人喜欢访问不同种类的POI，例如，有些人爱好美食，经常在不同的餐厅打卡，而有的人喜欢运动健身，他们更偏向去健身房、操场之类的地点进行锻炼.

5)地点流行度，一个区域的POI如果被人们签到过多次，表明至少它在当地非常受人们欢迎.本地用户的频繁访问为该地点增添了热度和知名度，这种流行现象直接影响异地的用户的出行计划，他们可能会慕名而来[9].文献[10]将地理位置融入核密度估计基础上，再结合兴趣点流行度特征和时间因素推荐，考虑了用户自身个性特征的同时体现了兴趣点的特征.由于目前大部分的研究只考虑到以上两种或三种影响因素，影响因素利用不够全面可能导致推荐准确率难以进一步提高.

除了以上提到的多种因素影响外，推荐系统仍存在用户/地点冷启动问题，即当一个没有签到记录的新用户或者一个新的POI进入系统时，系统无法得到它们的历史记录信息，就无法利用相似性进行推荐.

2 相关工作

最初经典的推荐算法是基于用户/地点的协同过滤[11，12]，利用用户/地理位置相似性预测用户的偏好程度择优推荐.传统的协同过滤没有考虑到多维的影响因素，继而出现了加入上下文语义信息的协同过滤[13]和融入地理、时间或社会影响的协同过滤[14].实际生活中，人们访问兴趣点的顺序存在一定行为规律，例如更多的人会在看完电影后去吃饭，而不是去运动，文献[15-17]在分析行为的顺序模式后得到了一系列连续性的POI推荐.随着通信时代数据量的剧增，为了解决数据量大且稀疏造成计算困难的问题，矩阵分解模型被提出，它利用数据间线性关系预测未知值，缓解了数据稀疏带来的预测困难.之后，随着数据集的不断完善，出现了加入时空影响或社会影响的矩阵分解模型[18-20]，推荐的准确率也有了明显提升，但目前大多数基于矩阵分解算法的推荐模型，仅利用了少量的影响因素，推荐系统在多维信息的联合利用方面仍有很大的提升空间.贝叶斯排序(BPR)算法[21-24]是基于矩阵分解的一种排序算法，针对每一个用户去过的兴趣点做排序优化推荐，虽然准确率有所提升，但没有做全局优化，无法向用户推荐其未访问过的兴趣点.

矩阵在数据建模的过程中会将原始数据转换成向量形式，如用户-地点向量，从实际物理含义来说，仅考虑矩阵形式会将多维数据的内部结构破坏.考虑到很多影响因素间具有一定的依赖性和联系性，在矩阵分解模型的基础上，衍生出了张量分解模型[25]，张量分解可以挖掘至少三种影响因子之间的潜在关系，在建模时就考虑到了数据的实际物理含义，例如，用户-时间-地点张量中每个元素的含义是用户在某个时刻某个地点是否有签到信息，且张量分解能有效缓解签到数据的稀疏问题.目前大多数基于张量分解的推荐算法[26-28]主要利用用户-时间-地点建模，以社会和空间条件作为约束项，采用CP分解或HOSVD分解进行优化.

表1 基本符号

Table 1 Basic symbols

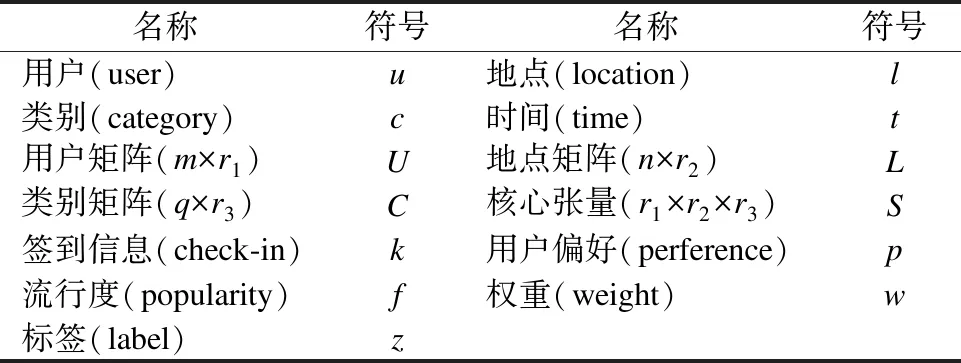
名称符号名称符号用户(user)u地点(location)l类别(category)c时间(time)t用户矩阵(m×r1)U地点矩阵(n×r2)L类别矩阵(q×r3)C核心张量(r1×r2×r3)S签到信息(check-in)k用户偏好(perference)p流行度(popularity)f权重(weight)w标签(label)z

针对现有研究中有待提升的点，结合张量分解算法的优势，本文提出一种基于张量分解的多维信息融合的兴趣点推荐通用模型.主要贡献点如下：

1) 提出了一个基于张量分解的多维信息融合的通用模型，该模型融合了时间影响、地理影响、社会影响、类别影响以及地点流行度影响，且模型灵活有可扩展性，允许直接增添新的特征维度.

2) 利用地点分类约束了张量的大小，将上万的地点规划至三十多种常用类别下，设计了用户-时间-类别张量，在基于HOSVD处理原始张量的基础上，结合梯度下降法对张量进行分解，缓解了签到信息的稀疏性.

3) 提出用户常驻地和标签偏好概念.设置与用户常驻地的距离阈值，区分本地和异地推荐.针对具体情况为影响因素分配不同权重，本地推荐侧重地理因素影响，异地推荐侧重于标签偏好.

4) 针对推荐问题中的用户/地点冷启动问题，本文有相应的解决方案.没有记录的新用户可利用社会关系在用户画像中找到与之相似的用户，系统为其推荐相似用户访问过的兴趣点.没有被签到过的兴趣点可通过在地点标签中找到与之距离较近的兴趣点，利用已知POI的流行度影响带动发展，一起推荐给用户.

3 模型描述

3.1 数据集及预处理

在以下实验中，本文使用了Foursquare数据集.在数据预处理阶段，删去了签到消息少于10条的不活跃用户以及签到信息不够完整的记录.

3.2 基本定义

表1是关于以下本文实验用到的基本符号的描述.其中矩阵和核心张量的尺寸在括号中给出.

表2是一个用户的一条签到信息的具体内容示例.

表2 签到记录示例

Table 2 Example of a check-in record

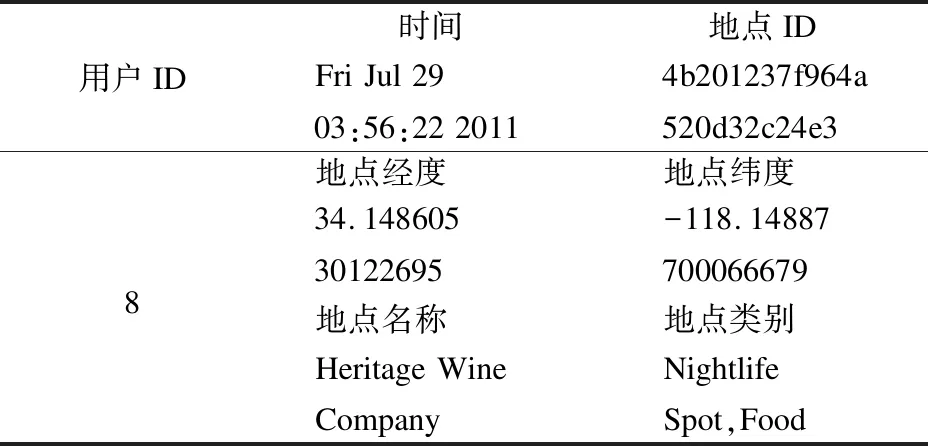
用户ID时间地点IDFri Jul 2903:56:22 20114b201237f964a520d32c24e38地点经度地点纬度34.14860530122695-118.14887700066679地点名称地点类别Heritage WineCompanyNightlifeSpot,Food

3.3 建模过程

3.3.1 模型框架

模型框架如图1所示，将数据集里的用户签到信息进行预处理，处理后的数据用于构造用户画像和地点标签.

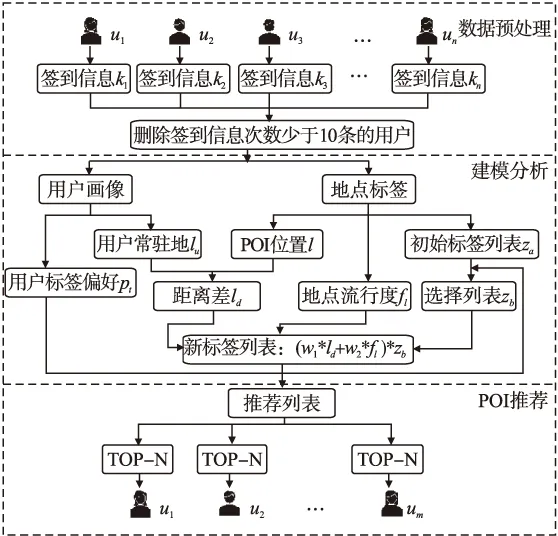
图1 模型流程图

第一部分，先构造用户-时间-种类的三阶张量，并且加入社交网络中的朋友关系作为张量模型中的约束项.该张量中每个元素的实际物理意义为用户u在时间t对兴趣点类别c的偏好程度，即用户对时间-类别标签的偏好度pt.接着，分析每个用户签到信息中的经纬度信息，找出一个点与签到信息中各地点的欧式距离和最小，作为用户“常驻地”lu.

第二部分，先记录每个POI的位置信息l(经度，维度)；再根据时间-类别特征定义标签，通过用户的签到记录将每个兴趣点(带有经纬度)划分到标签下得到初始标签列表za.其中，一个兴趣点可以对应多个标签，例如，有一个ID为“4b5b5cfdf964a520e9f728e3”的兴趣点可属于标签“周末下午-商店服务”，也可以属于“周末上午-食品”.统计每个兴趣点在系统中的签到次数，根据次数排名给每个兴趣点加上“地点流行度”fl，例如，排名第一的POI流行度为1，而倒数第一者流行度为0.01.

第三部分，利用HOSVD分解和梯度下降法得到预测后的新用户-时间-种类三阶张量，即得到了用户对标签的偏好值.接着，选出张量中排名前x大的元素值，以此挑选出za中的相应位置作为选择标签列表zb.最后计算用户“常驻地”与兴趣点间的距离差ld，结合地点流行度fl和选择标签列表zb加权计算得到TOP-N个POI推荐给用户.

3.3.2 用户画像

用户-时间-类别张量构造过程如图2(a)所示，其中，元素“1”表示用户在该时间-类别下有签到记录，元素“？”表示未知.根据签到次数在对应元素前加一个权重值后得到原始张量，原始张量的每个元素实际物理意义为用户对每个时间类别标签的偏好度，称之为用户标签偏好.

用户朋友关系如图2(b)所示，我们认为用户ui和朋友uj间去过的相同POI重合度越高，则他们之间的偏好越接近.用户i和朋友j的相似度通过以下相似度计算公式得到，

(1)

其中，Gui和Guj分别表示用户ui和朋友uj签到的POI集合.f(·)为补偿函数，|Gui-Guj|越大则补偿数值越大，补偿数值逐渐趋于平缓，经过实验选择，f(x)=log2(x+2)适合用于本文提出的模型.

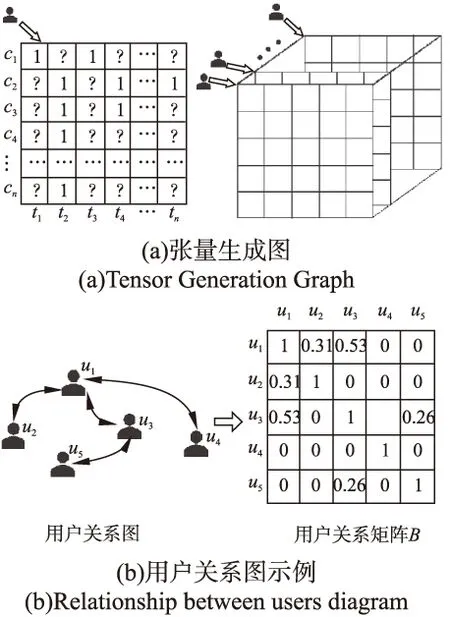
图2

大部分研究根据兴趣点地理位置远近做推荐，通常只会推荐距离较近的地点，而未考虑对用户进行本地和异地推荐，因此，本文提出用户“常驻地”概念，常驻地lu表示为，

(2)

其中，Lu={l1,l2，…，ln}为用户u去过的地点集合.

对于每个用户而言，找到一个中心点，使用户签到信息中所有地点与该点欧式距离和最小，将该点作为常驻地；以常驻地为中心，计算常驻地与POI之间的距离差；设置距离阈值，阈值范围之内的兴趣点在推荐时侧重于地理因素影响，而阈值范围外的兴趣点则侧重于用户偏好影响和地点流行度影响.

3.3.3 地点标签

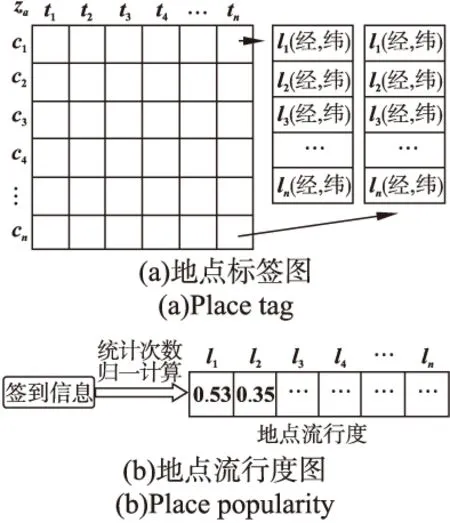
图3

初始标签列表如图3(a)所示，时间-种类标签下存有对应兴趣点ID及位置信息.地点流行度生成图如图3(b)所示，统计每个地点出现的次数并做归一化计算.

4 张量分解方法

4.1 HOSVD

目前许多关于张量分解的研究工作主要采用两种方法：CP分解和Tucker分解.其中，Tucker分解通常会采用高阶奇异值分解(Higher Order Singular Value Decomposition，HOSVD). 如图4所示，本文首先采用HOSVD分解原始用户-时间-类别张量，提取张量中重要特征，尽管HOSVD能够起到降维和缓解数据稀疏的作用，但它并不能很好地处理缺失的数据信息.因而，在利用HOSVD处理原始张量的基础上，再进行分解，以便很好地补全丢失信息.

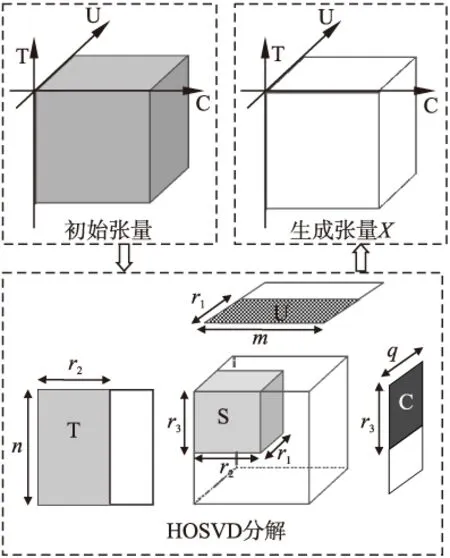
图4 HOSVD示意图

X=S×UU×TT×CC

(3)

其中，S∈Rr1×r2×r3，U∈Rm×r1，T∈Rn×r2，C∈Rq×r3

4.2 损失函数

(4)

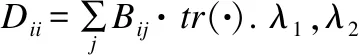
4.3 张量分解过程

由于目标函数(4)是非凸问题，寻找目标函数的最优结果没有封闭形式的解，使用随机梯度下降(SGD)来查找局部优化.

(1)计算Yijk=S×UUi*×TTj*×CCk*

(2)分别计算关于S,U,T和C的梯度值：

∂UFls(Xijk,Yijk)=(Yijk-Xijk)×S×TTj*×CCk*∂TFls(Xijk,Yijk)=(Yijk-Xijk)×S×UUi*×CCk*∂CFls(Xijk,Yijk)=(Yijk-Xijk)×S×UUi*×TTj*∂SFls(Xijk,Yijk)=(Yijk-Xijk)×Ui*⊗Tj*⊗CCk*

算法1.张量分解算法

输入:张量X，矩阵B

输出:S，U，T，C

1.用较小的随机数初始化S∈Rr1×r2×r3,U∈Rm×r1，T∈Rn×r2

C∈Rq×r3

2.设置步长η

3.for每一个不为0的Xijkdo

4.Yijk=S×UUi*×TTj*×CCk*

5.Ui*←Ui*-η∂UFls-ηλ1Ui*-ηλ2LBUi*

6.Tj*←Tj*-η∂TFls-ηλ1Tj*

7.Ck*←Ck*-η∂CFls-ηλ1Ck*

8.S←S-η∂SFls-ηλ1S

9.end for

10.returnS，U，T，C

5 实验分析

本节将详细描述实验数据和内容，展示实验效果图，并对实验结果进行分析.

5.1 评价指标

本文实验选取了Foursquare数据集，对于每个用户，我们随机选择其签到信息的70%构成模型训练集，剩余30%作为验证集.训练后的模型可得到每个用户排名为TOP-N的兴趣点并推荐给用户.为了评价实验的性能，我们采用以下两个指标：

准确率：

召回率：

其中，N表示给用户u推荐的POI个数，M为总用户数量，Su为推荐给用户u的TOP-N兴趣点的集合，Vu是用户u访问的地点集合.上述指标对应于一个试验，推荐算法的最终性能通过5次独立试验的平均指标得出的.

5.2 实验结果

5.2.1 用户常驻地聚类图

图5中每个圆点表示用户签到过的一个地点，五角星表示用户常驻地.

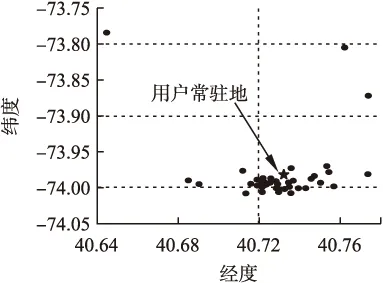
图5 单个用户常驻地示例

5.2.2 张量分解损失值图

图6表明迭代次数超过20次后，矩阵U，T，C及核心张量S的损失值变化趋于平稳；图7显示迭代次数超过15次后，张量损失函数值逐渐收敛.

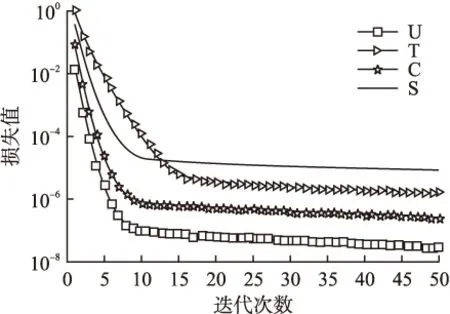
图6 矩阵及核心张量损失差值图

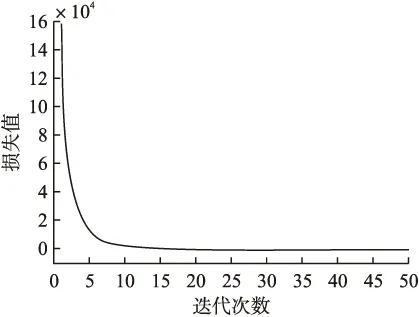
图7 张量损失函数图

5.2.3 对比实验

本文在张量分解的基础上主要利用了地理位置、时间因素、社会关系和地点流行度因素，提出一种基于张量分解的多维信息融合兴趣点推荐算法(Multi-dimensional Information Fused Point-of-Interest Recommendation based on Tensor Decomposition，MIFTD)，选取以下算法作为对比：

对比实验1：基于时间权重的矩阵分解推荐算法(Time Matrix Factorization，简写为TMF)，该算法中考虑了时间，朋友关系和地理因素，根据人们在不同时间段的访问活跃度给矩阵元素加上时间权重[29].

对比实验2：基于加性马尔科夫链的推荐算法(Additive Markov Chain，简写为AMC)，该算法中融合了朋友关系、时间影响、地理因素以及地点流行度[30].

表3为N=5时，三种算法的实验准确率和召回率具体数值.

表3 N=5时，推荐准确率最高

Table 3 N=5，the highest recommendation accuracy

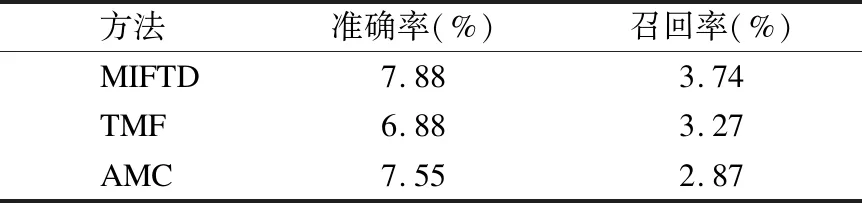
方法准确率(%)召回率(%)MIFTD7.883.74TMF6.883.27AMC7.552.87

由图8和图9可知，随着N取值的增大，推荐算法的准确率呈现下降趋势，召回率呈现上升趋势.对比推荐表现相对较好的TMF算法，在5次不同的N取值下，本文算法平均推荐准确率提升了约17%.

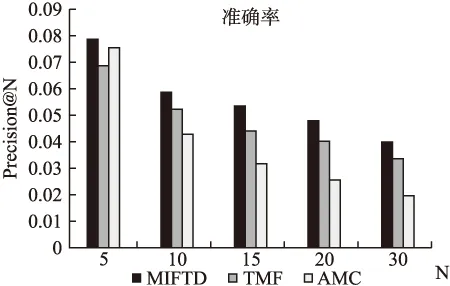
图8 准确率对比图

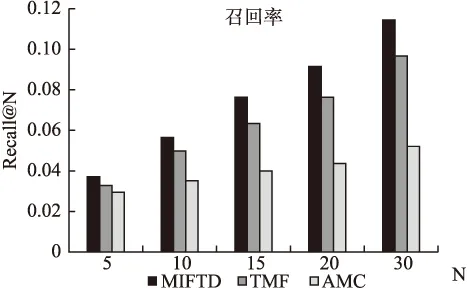
图9 召回率对比图

6 结束语

本文提出了一种基于张量分解的多维信息融合的兴趣点推荐通用算法，用户画像中提出用户常驻地概念，利用三阶张量融合时间、社会关系和类别影响，地点标签中利用了地理影响和区域流行度影响，结合两者并为影响因素分配权重得到最终推荐的TOP-N兴趣点.该模型灵活通用，方便增添新的特征维度，且有效解决了数据稀疏和冷启动问题.考虑到用户行为顺序特征，即通常人们访问POI具有一定的先后顺序规律，所以推荐兴趣点还应当注意时序问题.