借助习题可视化,发展学生高阶思维
2020-05-13潘旭英
潘旭英
【摘要】有效的练习设计有助于学生融通知识脉络,是培养学生思维能力,锻炼学生思维的一种很好的途径。要落实学生的核心素养,教师就要设计能看见过程性的作业,能看见学生思考和审视学生思考过程的作业。借助图示的解读方法,发展学生的高阶思维。
【关键词】图示 可视化 高阶思维
数学是思维的体操,知识习题的练习过程是培养学生思维能力,锻炼学生思维的很好的途径。但是,小学数学中的很多作业呈现的只是思考的结果。要落实学生的核心素养,教师就要设计能看见过程性的作业,尤其是能看见学生思考和帮助学生审视自己思考过程的作业。特别是复习课的练习设计,要在用足习题的基础上,合理地解析每道有效习题的内在价值。在此基础上承构新习题,做到化题为组,力求让学生通过练习达到做一题会三题,练一组会一片的效果。多样化的练习设计也可以达到复习课梳理知识、重构认知的目标效果。
以小学数学“多边形面积”单元为例,主要教学平行四边形、三角形和梯形的面积计算。(一)运用转化思想,根据图形间的内在联系推导面积计算公式;(二)加强动手实践、自主探索,让学生经历知识的形成过程;(三)在解决实际问题中渗透估测意识、策略。以上三点教材建议重在运用转化思想,建立图形间的内在联系,让学生经历知识的形成过程。
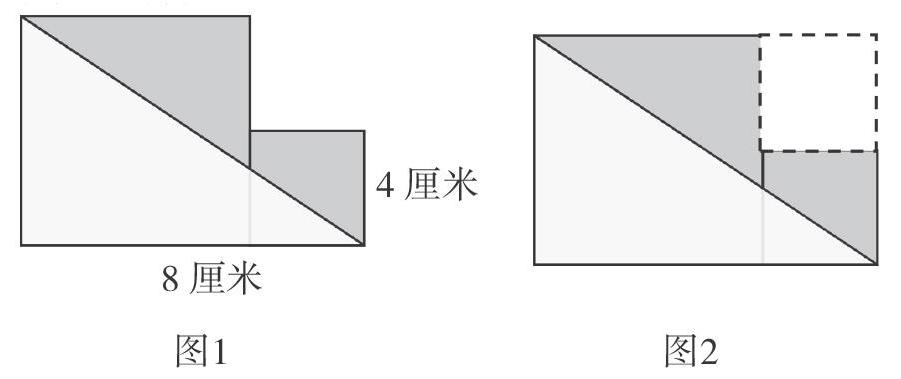
【习题呈现】在练习中,有这样一题(如图1):
求阴影部分的面积。
学生在解答这道题时,根据题中的已知条件,大、小正方形各为8厘米、4厘米,基本得出:阴影部分的面积=大、小正方形面积和-三角形的面积,或还有学生利用拼补一个小正方形(如图2),得出阴影部分的面积=一个三角形面积-一个小正方形的面积。本题考查学生对组合图形面积的灵活解决,笔者认为此题的思维价值还可以继续深层挖掘。因此在单元复习课的练习设计中,笔者尝试运用图示的解读方法,发展学生的高阶思维。
一、变化基础题:知识统整, 形成网络
立足学生核心素养提升的教学需要课堂转型,练习设计也要随之转型,有效的作业设计是巩固新学知识和技能的前提。大多练习设计都从“双基”目标达成出发,通常会从教材例题或教材练习中设计相似题型的练习,用于学生巩固新知,掌握基本基础技能。“双基目标设计策略”根据题目中的已有问题解决需要的已知条件,再进一步解决问题,也就是学生课堂上学什么,练习就练什么,条件和问题都是由教师给定。但纯讲解練习并不能有效地帮助学生复习知识,借助图示,通过可视化的形式,可以更好地在比较中帮助学生有效统整单元知识,形成知识网络。
【设计呈现】
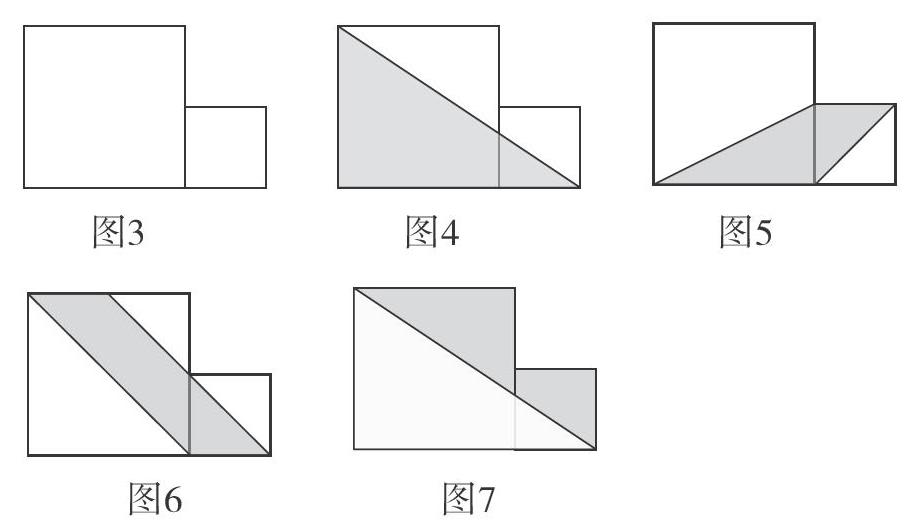
两个大小不同的正方形,连接其中的一部分顶点,可以产生很多的组合图形。先让学生画一画,再小结图示,进行练习。
如果大正方形的边长为8厘米,小正方形的边长为4厘米。你能求出各图中阴影部分的面积吗?
【案例回放】
生1:找到阴影部分(三角形的底和高)。
(8+4)×8÷2=48(平方厘米)
生2:找到阴影部分(梯形的上底、下底和高) 。
(8+4)×4÷2=24(平方厘米)
生3:找到阴影部分(平行四边形的底和高)。
4×8=32(平方厘米)
生4:方法一:用2个正方形面积减三角形面积。
8×8+4×4-(8+4)×4÷2=32(平方厘米)
生5:方法二:用三角形面积减空白小正方形面积。
(8+4)×4÷2-4×4=32(平方厘米)
师:要求出这些阴影部分的面积,关键是什么?
生:找出它们的指定的底和高。比如图4找三角形的底是8+4=12厘米,高是8厘米;图6底是4厘米,高是8厘米……
【执教反思】
以上是在原题基础上设计了组合图形面积计算,学生只要记住并理解各基本图形的面积计算方法以及所要找寻的已知条件,就能比较简单地解决问题(就如案例回放)。相对于变式或拓展题型,基础性习题仍是学生基本技能培养的重要方式之一。基于“双基目标”进行的设计,它可以满足大部分学生对本单元基础知识的掌握与基本技能的形成。运用图示,画——打开学生的思维,图——呈现思维的过程,这样的解答过程可以将单元知识进行梳理,并帮助学生形成统整的一种知识链,在基础题型的层面上提升了学生的思维。
二、创新一般题:呈现过程,跃进深度
创新,是学生核心素养中最重要的能力之一。一位特级教师这样分享自己的经验:“数学教师要让学生在课堂上尽可能积累必要的知识,多了之后,尽可能把所有知识连起来;更要引导孩子们不断地把大脑中沉淀已久的东西清空,让大脑有足够多的空间发展新的智慧。”“创新一般图示”就是让学生运用已有的知识经验创造性自主设计练习,借助图示可视化的特点,呈现思考过程,跃进思考深度。这也是数学教学中学生创新素养提升的有效途径。
【设计呈现】自主设计创新习题
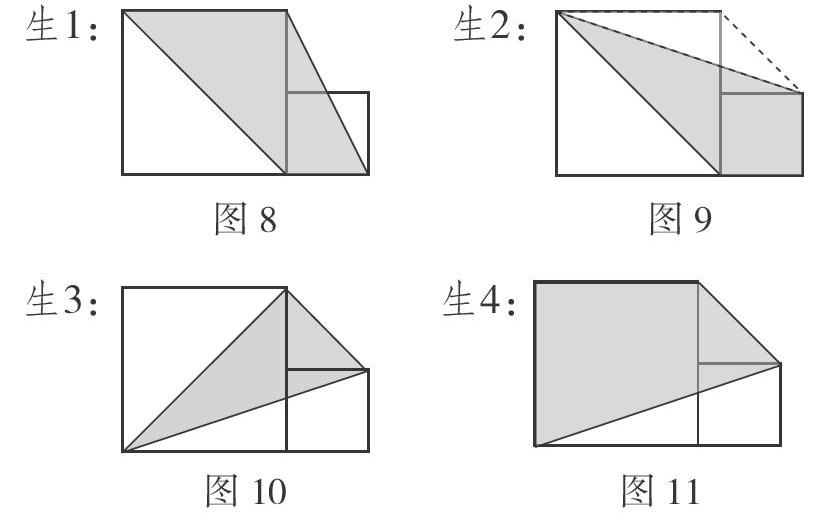
(承接上题)除了以上这些图形外,你还可以自己设计不同的组合图形。请你试着设计几种,并求出阴影部分的面积。
【案例回放】
生独立计算,指名学生上台展示。其他同学适时评价。
【执教反思】
习题是教学活动实现的重要依据,它不仅显示具体的“知识”资源,而且隐含丰富的“思维”资源,让学生自主进行创造性开发,更是其创新能力的发展。让学生自主设计作业练习,借助图示表现可以降低学生的抗拒感,同时也尽可能减少所谓的解题引导,允许学生结合自己的已有经验和个体理解,对练习的呈现、知识的考量作出自己的判断。因为学生有知识经验、思维经验以及认知风格的差异,因此自主设计的练习会出现不同的思维层次。比如,图8属于基本图形的设计,稍复杂的图10、11组合图形,一般学生都能找到相应条件,而图9则可能需要添辅助线,找到虚线的三角形,从而求出阴影部分面积。在这样的一个过程中,图示展现,呈现了班级学生的思考过程,再通过解答练习就推进了学生的思维深度。
三、拔高对比题:结构思考, 阶梯生长
随着学生学习能力的不断提高,对于基础的知识和技能学生完全靠模仿和记忆显然是不够的。创新能力的发展也需要依托学生的认知,再在此基础上进行提高型设计,通过习题间的对比、联系,发挥习题的更大价值。学生掌握数学知识,主要靠抽象思维,但没有形象思维的配合与支持,解决问题就很困难。“拔高对比图示”是教师基于学生的认知,在学生创新基础上再拔高,通过一组对比或提高练习,感悟数学的内在思维价值,发展学生的高阶思维。
【设计呈现】提高设计
如果将生3的图10中小正方形边长分别改成5厘米(图12),6厘米(图13),其余条件不变,画出类似的阴影图形,请计算它们的面积,你有什么发现?
【案例回放】
学生尝试计算,说说自己的发现。
生1:图10阴影部分面积=8×8÷2+4×4+4×4÷2-(8+4)×4÷2=32(平方厘米)
生2:图12阴影部分面积=8×8÷2+5×5+3×5÷2-(8+5)×5÷2=32(平方厘米)
生3:图13阴影部分面积=8×8÷2+6×6+2×6÷2-(8+6)×6÷2=32(平方厘米)
師:算到这里,你有什么问题?
生4:为什么面积都是相等的?
生5:阴影部分面积正好是大正方形面积的一半,这是为什么呢?
生6:阴影部分面积是不是和小正方形无关?
……
【执教反思】
同样是多边形的面积,在大正方形保持不变、小正方形变化的情况下,同样三个点连接形成的阴影部分面积都相等,而且面积正好等于大正方形的一半。这样的拔高设计引发了学生的诸多思考:明明小正方形在变,为什么阴影部分面积相等?阴影部分面积为什么是大正方形面积的一半?阴影部分面积是不是和小正方形无关?……此题虽然仍旧是阴影部分面积的计算,但是考量的不仅仅是面积,更多的是指向于面积相等背后的深层思维,引发了学生诸多有价值的思考。笔者也发现,当图示呈现对比后,学生的有效思维大大提高。
课标指出:“根据评价的目的合理地设计试题的类型,有效地发挥各种类型题目的功能。”本题是在学生学习“多边形的面积”后的一个练习,利用两个大小正方形各个顶点的连接变换出不同的阴影部分,目的是为了检查学生对基本图形面积的掌握能力,要学生善于从较复杂的图形中找出基本图形的特征,求出阴影部分的面积。同时为了考查学生的创造能力,学生也可以自己设计,最后通过对比,寻找共性。在设计时,借助图示,将知识可视化,思考可视化,一题变为一组,在用足习题的基础上,合理地解构习题的内在价值。一道习题,经过改造后,既带来了知识本身的多样变式,又带给学生技能的提高,更引发了学生的有价值思考。
【参考文献】
雷玲.名师作业设计新思维[M].上海:华东师范大学出版社, 2017.