让复习充满“生长”的力量
2020-05-13高敏
高敏

【摘要】图形领域的复习,应沟通“理”和“练”,让复习更深刻;应抓住“漏”和“缺”,让复习更有效。重视对数学知识的理解、方法的提炼、思想的感悟、思维的提升,使复习充满“生长”的力量。
【关键词】沟通 抓住 生长
图形领域的内容,在小学阶段涵盖各册教材,是小学数学教学中的重要组成部分。除了巩固图形的特征以及计算方法,沟通与生长才是图形复习课的主旨。
一、沟通“理”和“练”,让复习更深刻
复习过程中的“理”和“练” 缺一不可,“理”是为了抓住知识的本质以及知识间的联系,形成良好的认知结构;“练”是为了知识体系的完善以及应用能力的提高,学会数学地思维。
1.理得深刻是为了练得清楚
笔者在复习“立体图形”时,课前布置学生自主整理立体图形的知识,有的学生只是书本概念的“搬运工”(如图1和图2),有的学生已经有了一些思考,注意到了图形之间的联系——直柱体统一的体积公式(如图3)。
知识的整理如果只是成为复习的一种形式,那就失去了整理的价值。只有启发学生抓住知识的内在联系,串点成线,积珠成链,从不同角度、不同层次展开触动思维的整理,为“练”扫清障碍才是知识整理的最终目的。
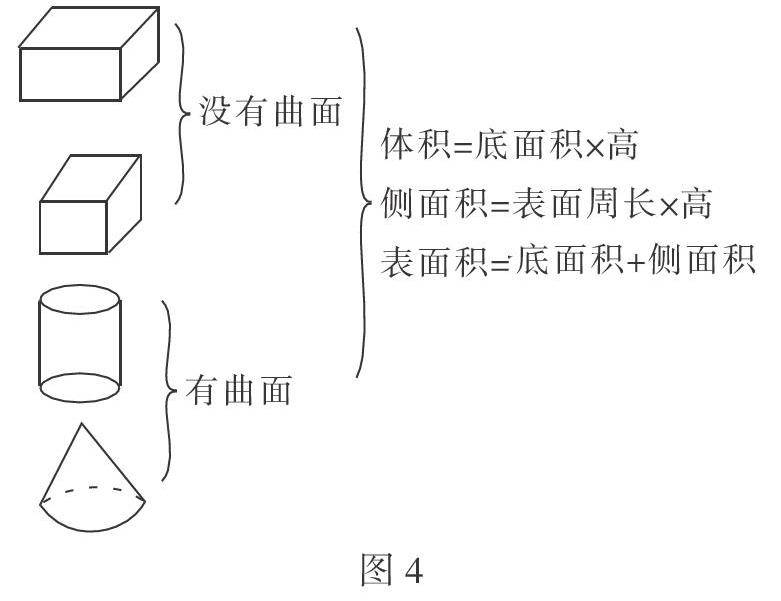
“哪些立体图形可以分一类?”的追问,有了课堂上的整理。图4从“有无曲面” 这个特征将四个立体图形分成了两类,也从计算方法出发,把长方体、正方体和圆柱分一类。学生的思维此时不停地向深处漫溯:我认为凡是直柱体,求体积都可以用底面积×高来计算;我在思考圆锥的体积为什么不能用“底面积×高”来计算……
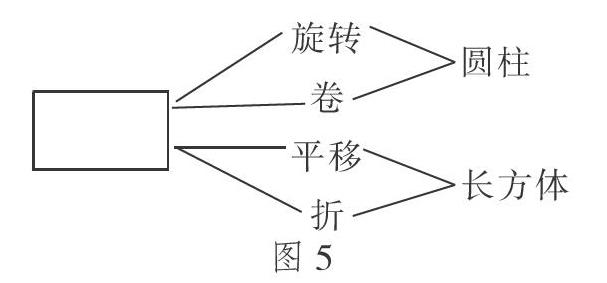
图5的整理引起了学生们的极大兴趣,通过小组成员旋转、卷、折等实际操作,进一步解决了如下问题:
①长方形可以通过不同的方式得到一个立体图形,这个立体图形与长方形之间有什么联系?
②长方形旋转成一个圆柱,除了绕着长或宽旋转,还可以绕哪条边旋转?得到的圆柱与长方形有怎样的联系?
③长方形垂直平移形成长方体,正方形平移得到正方体,像这样的图形你还能想象出几个?
复习课的“理” 不能只流于形式,更重要的是理得深刻,理得透彻,从简单的“概念知道”迈向深刻的“智性思考”。温故而知新,为学生开启一个新的观察、新的视角,才能提升复习课的品质。
2.练得提升是为了理得透彻
教学过程:学生由等底等高的三角形面积相等联想到等底等高的平行四边形面积也相等,又产生等底等高的梯形面积是否也相等的探究欲望。
师:梯形的等底等高是什么意思,谁来解释?
生1:梯形的等底等高就是上底下底和高的长度都一样。
生2:我不同意你的想法,等底,我这样理解——就是两个梯形上底加下底的和合起来是一样的意思。
生3:我也这样想,我还举了些数据,比如两个梯形高都是4厘米,一个梯形上底1厘米,下底5厘米,另一个梯形上底2厘米,下底4厘米,它们的面积就是一样的,因为高相等,底的和也相等,这就是等底等高。
……
随着探究的深入,学生又有了这样的想法:把三角形想成上底为0的梯形,把平行四边形想成上底和下底相等的梯形,也可把长方形、正方形想成梯形,整理成同一个面积计算公式:(上底+下底)×高÷2。这样使得复习有意思、有味道、充满趣味,达到复习一点懂得一片,理解一片贯通一面的目的。
二、抓住“漏”和“缺”,让复习更有效
很多学生对复习课不感兴趣,原因是教师不了解学生的学习基础,仅有温故不能知新;不了解学生的学习需求,学生解决了的问题还在上面纠缠,困惑的问题又不去涉及。所以复习的有效,还必须认真抓住学生的“漏” 和“缺” 。
1.寻找“漏”和“缺”
图形内容的复习,究竟是求容积、侧面積、表面积还是体积是学生不容易分清的,题目中单位不同是学生容易忽视的……所以复习的查漏补缺很重要。课堂练习、单元检测等出现的典型错题都是教师可以查找的“漏” 和“缺” 。但,教师寻求到的“漏”就一定直抵学生的“漏” 和“缺”吗?不一定。所以,学生自行寻找“漏”和“缺”的过程也十分重要。学生自己整理的易错题,教师应认真阅读,判断解答正确与否,分析易错点的来源:是基础知识没掌握,是空间观念形成有困难,还是非智力因素导致的错误,然后在复习的教学中有意识、有重点地去渗透。
2.突破“漏”和“缺”
为了突破解决实际问题中出现的易错点,可以出示这样一道题:这是一个底面半径10厘米,高30厘米的圆柱形木桩(如图6)。根据提供的数据,你能提出哪些相关的问题呢?小组内交流,然后解答。
针对学生提出的有关表面积和侧面积的问题,追问:在平时遇到的实际问题中,什么时候只要计算侧面积?什么时候又要计算侧面积和一个底面积呢?
在解决一道题后,一定要有延伸的过程,避免讲完就万事大吉的习惯,因为只有在不断变化中学生才能对知识有更深刻的理解。
根据上题可以有这样的延伸练习:让学生对这个木桩进行适当的加工改造,再提出一些数学问题。
学生提出的问题:把这个木桩削成一个最大的圆锥,这个圆锥的体积是多少?削去部分的体积是多少?
对应的练习:(1)把一个圆柱削成一个最大的圆锥,削去部分的体积是6立方厘米,原来圆柱的体积是(),削成的圆锥体积是 ()。
(2)如果把这个木桩削成如图7所示的一个陀螺,它的体积又是多少?(重点让学生体会等积变形的思想)
学生提出的问题:(1)把这个木桩沿着底面直径和高截成两半,表面积增加多少?(2)把这个木桩沿着与底面平行的方向截成两段,表面积增加多少?
对应的练习:一根圆柱形木材长3米,将它锯成长度相等的2段,表面积增加了180平方厘米。每段木材的体积是多少立方厘米?
学生对知识的习得、意义的理解,在每个学生的学习过程中需要有自主的复习意识、能力和行动,查漏补缺的过程不只是唤醒“缄默”的知识,而是在独立思考、交流碰撞、构建知识体系、提高运用能力中达到复习查漏补缺、提升能力的目的。
此外,也可以让学生多说说“我的困惑”“我的提醒”“我的反思”,在复习课中多看到学生才能让学生走出迷津、走向成功。
图形复习应关注学生对数学知识的理解、方法的提炼、思想的感悟、思维的提升,使复习充满“生长”的力量。