PBX稀疏CT投影PICCS图像重建算法

张建伟，张才鑫，陈 华，张 韬，4，刘 晨，刘丰林

（1.中国工程物理研究院化工材料研究所，四川 绵阳 621999；2.重庆大学光电技术及系统教育部重点实验室，重庆 400044；3.重庆大学工业CT 无损检测教育部工程研究中心，重庆 400044；4.哈尔滨工业大学计算机科学与技术学院，黑龙江 哈尔滨150001）

1 引言

高聚物黏结炸药（Polymer Bonded Explosive，PBX）是一种由炸药晶体、黏结剂等构成的多组份复合材料，因其性能优良广泛应用于武器装备。PBX 在加工成型过程中，不可避免地存在孔洞、气泡等初始损伤［1］，这些损伤在应力影响、存放环境等多因素相互作用下，易形成不同程度、不同形态、不同扩展方式的裂纹［2-3］，影响 PBX 的力学性能、爆轰性能以及安全性能［4-5］。因此，对PBX 炸药件初始损伤以及裂纹进行检测，将有利于保证PBX 性能以及运输储存过程中的安全性。当前，对于PBX 炸药件初始损伤以及裂纹检测主要采用的是计算机断层成像（Computed tomography，CT）技术，在实际检测中，CT 扫描过程需要采集一定数量投影数据，这个过程需要较长时间，检测效率低。因此，亟需研究一种提高检测效率的方法。稀疏投影CT 扫描的方式可减少投影采集时间提高检测效率。但稀疏CT 投影是典型的不完备CT 投影，从不完备投影集重建图像存在噪声大、伪影严重、细节模糊等问题，影响对检测物体内部结构和缺陷的观察、判断。因此，在稀疏投影提高检测效率的前提下，选用合适的重建算法来保证重建图像质量至关重要。

CT 投影重建方法可分为两类，一类是传统解析算法，其最具代表性的是滤波反投影重建算法（Filtered back projection，FBP），但它对投影数据的完备性要较求高；另一类是迭代重建算法，其代表性的方法有代数重 建 算 法（Algebra Reconstruction Technique，ART）［6］和联合代数重建算法（Simultaneous Algebra Reconstruction Technique，SART）［7］。 ART 和 SART算法放宽了对投影数据完备性的要求，但计算量大，重建速度慢，噪声较大。压缩感知（compressed sensing，CS）［8］理论的出现为 CT 图像重建提供了新的思路。Sidky［9］利用图像在梯度变换域内具有稀疏性这一先验知识，提出TVM-POCS（Total Variation Minimization-Projection Onto Convex Sets，TVM-POCS）重建方法，并成功用于稀疏角图像重建，但在重建图像轮廓附近存在严重的滑坡伪影。之后对上述算法进行改进提出自适应最速梯度下降-凸集投影算法（Adaptive Steepest Descent Projection Onto Convex Sets，ASD-POCS）［10］，以罚函数的形式增强解的稳定性，有效抑制了条形伪影，但收敛速度慢。Chen 等［11］通过在重建模型中引入先验图像，提出了基于先验图像约束的压缩感知图像重建方法（Prior Image constrained compressed Sensing，PICCS），与上述算法相比，该方法收敛速度快，噪声小，它通过引入先前扫描的CT 图像作为先验信息，可以大幅提高重建图像质量，使从更稀疏的投影集中恢复高质量图像成为可能。

为了提高检测效率，本研究利用稀疏采样的CT 扫描方式获得投影数据，采用PICCS 重建算法对稀疏投影数据重建抑制噪声，减少伪影，采用准静态单轴压缩TATB 基PBX 的损伤试件验证采样方式和重建算法，研究内容包括：（1）CT 重建模型和PICCS 算法重建模型；（2）准静态单轴压缩TATB 基PBX 的损伤试件的稀疏投影CT 扫描重建实验，以及对完备投影集FBP 重建结果与稀疏投影集SART、PICCS 两种算法重建结果进行对比研究。

2 PICCS图像重建算法

CT 重建的数学模型［12］可以归结为：

式中，A=(amn)表示系统矩阵M×N，M代表投影个数，N代表重建图像的像素个数表示投影向量表示重建图像向量，等式（1）可以通过迭代进行求解。但重建稀疏投影数据时，M通常是比N小，等式（1）是欠稳定系统，有无穷多组解。

正则化方法的提出有利于模型（1）从无穷多组解中找出满意的最优解，利用正则化方法，模型（1）可转化为如下最优化问题［11］：

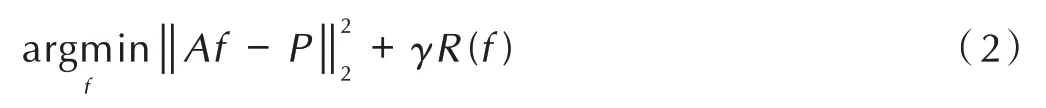
PICCS 算法重建模型［11］可表达为如下：

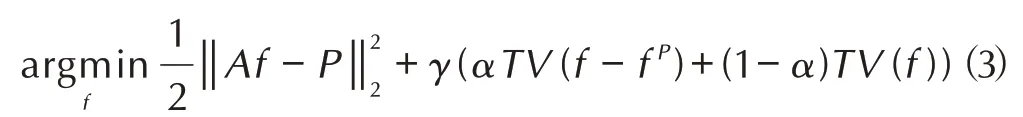
式中，fP表示高质量先验图像向量，TV是稀疏算子，α(0 ≤α≤1)是平衡参数，由先验图像质量确定，先验图像质量越好，α越接近1。在PICCS 算法中，先验图像的好坏将决定重建图像的质量，为了获得高质量的先验图像，一般采用滤波反投影（FBP）算法对较完备的投影进行重建。

采用PICCS 算法重建模型，稀疏算子选用全变分（Total Variation，TV）变换，TV 求解的是图像梯度 1范数，其表达式［9］如下：

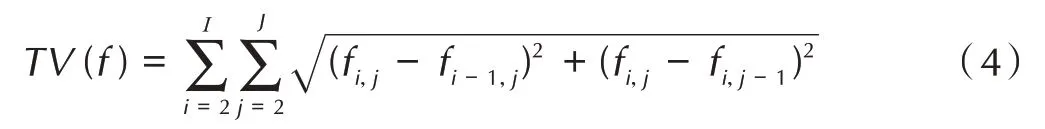
式中，I和J分别是重建图像的长和宽，单位为 pixel；fi，j是重建图像栅格(i，j)坐标上的像素值。

3 准静态单轴压缩试验与CT扫描重建实验

3.1 试验样品

检测样品为Φ10 mm×15 mm 的 TATB 基 PBX 圆柱形试件，由中国工程物理研究院化工材料研究所提供。

3.2 准静态单轴压缩试验

准静态单轴压缩试验在Instro 5582 万能材料试验机上完成，将检测样品放置于材料试验机上进行单轴压缩试验，位移控制速率0.05 mm·min-1，准静态加载至破坏。力学试验结束后将样品从材料试验机取下，进行离线CT 扫描重建实验。

3.3 稀疏投影CT扫描重建实验

为了验证PICCS 算法对于高聚物粘结炸药不完备投影重建的可行性，分别采集不同稀疏程度的不完备投影集，用SART、PICCS 二种重建算法进行重建，将它们与完备投影集的FBP 重建结果对比，最终得出PICCS 重建算法在满足对检测物体缺陷和内部结构观察、判断的前提下，可以用稀疏几倍的投影集重建出满足要求的图像，进而提高几倍检测效率。

CT 扫描重建实验所用设备如下，电脑：Intel（R）Core（TM）i7-67 CPU @ 3.40GHz、8.00GB 内存；编程 环 境 ：MATLAB R2017a；CT 设备 ：nanoVoxel 设备（中国天津三英精密工程研究中心）。

实验扫描参数如表1。对其进行准静态单轴压缩试验，然后对试件进行稀疏投影CT 扫描重建实验观察其内部裂纹分布。试件压缩后采集数字X 线摄影图（Digital Radiography，DR）如图1。SART 算法初始图像为零，PICCS 的先验图像是通过扫描破坏前的试件采用SART-TV 迭代500 次得到，如图2。

表1 扫描参数Table 1 Scanning parameters

图1 CT 重建 实 验 PBX 试件 DR 图FFiigg.1 Digital radiography（DR）image of PBX Specimen reconstructed by CT scanning

图2 试件破坏前CT 扫描重建得到的先验图像FFiigg.2 Specimen image prior to its failure reconstructed by CT scanning

在实验中，把720 个投影FBP 重建结果作为参照图像，稀疏投影CT 扫描分别均匀采集3 组不同投影数n=360，240，180 的投影集进行重建实验，角度增量分别是d=1°，1.5°，2°，分别对应 FBP 投影集稀疏倍数m=2，3，4，SART 迭代 100 次收敛，PICCS 迭代 20 次收敛。为了清晰地观察重建图像中细小裂纹，把重建结果适当放大，如图3 所示。从图3 可以看出，SART 重建算法受噪声影响较大，在稀疏3 倍时，细小裂纹被噪声淹没，但稀疏2 倍时，图3（b）中箭头所指细小裂纹可以被SART 重建出来，所以SART 可以用稀疏2 倍的投影集重建满足要求的图像；而PICCS 重建算法受噪声影响较小，重建图像比较平滑，在稀疏4 倍时，重建图像出现少量伪影，箭头所指裂纹被伪影覆盖，无法满足检测要求，但稀疏3 倍时，PICCS 算法可以重建出箭头所指的细小裂纹，图像满足科研观察要求。主观视觉判断PICCS 算法用稀疏3 倍的投影重建结果与720 个投影FBP 重建结果相近。每个算法重建出满足要求的图像所需的投影数量以及所需的时间如表2 所示。虽然迭代重建时间要比FBP 重建时间长，但是随着计算机硬件的提升以及GPU 并行计算的出现，迭代重建时间会大大减少。

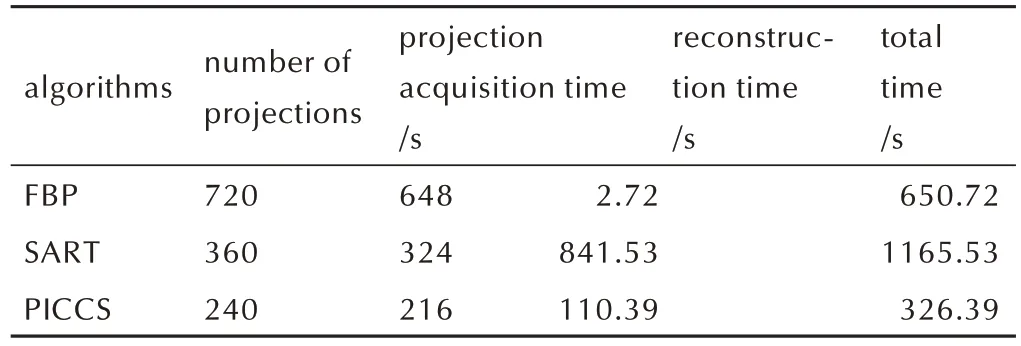
表2 各算法重建结果满足要求所需时间Table 2 Time required for the reconstruction of each algorithm to meet the requirements

为了能够更清晰地看到PBX 细小裂纹的重建情况，更加准确地判断SART、PICCS 算法能够利用稀疏几倍的投影重建出满足要求的图像，分别把图3 中m=3，4 时（d）（e）（f）（g）（h）（i）矩形区域放大，如图 4所示。图4 可以清晰地看到m=3 时，SART 重建图像中箭头所指裂纹被噪声淹没，不利于观察和判断，而PICCS 算法在m=3 时可以清晰重建出细小裂纹，但m=4 时，PICCS 算法重建图像中箭头所指裂纹模糊不清，所以，主观视觉判断PICCS 算法用稀疏3 倍的投影可以重建出满足要求的图像。

图3 完备投影FBP 和稀疏投影不同算法重建结果对比Fig.3 Comparisons of reconstructed results between complete projection FBP and sparse projections algorithms

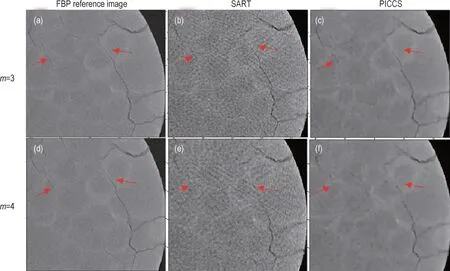
图4 对应图3 中m=3，4 时矩形区域，不同方法重建结果局部放大图Fig.4 Local enlargement of reconstructed results by different methods correspondingly to the rectangular region of m=3，4 in Figure 3

为了定量比较1/3 稀疏投影PICCS 和SART 的重建结果与720 个投影FBP 重建结果，分别计算它们的均方根误差（Root Mean Squared Error，RMSE）［13］、峰值信噪比（Peak Signal to Noise Ratio，PSNR）［13］，表达式分别如式（5）（7）所示。

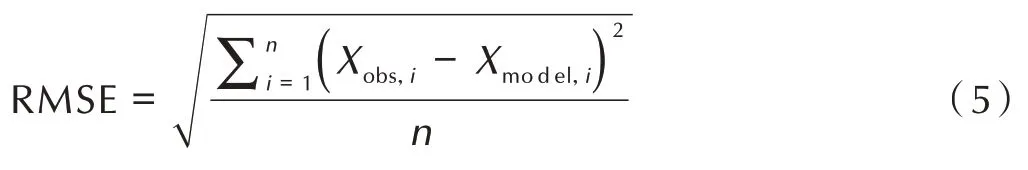
式 中 ，RMSE 是 观 测 值Xobs，i与 真 值Xmodel，i偏 差 的 平 方和观测次数n比值的平方根。RMSE 值越小，重建结果越精确。

式中，MSE 表示当前图像X和参考Y的均方误差（Mean Square Error）［13］，I和J分别是图像的高度和宽度，n为每像素的比特数，一般取8，即像素灰阶数为256，PSNR 单位是dB，数值越大表示失真越小，重建图像质量越好。

对于重建图像，感兴趣的是重建物体内部结构和缺陷，而重建图像中重建物体之外的信息不关心，所以为了更精确的进行定量计算，把1/3 稀疏投影PICCS和SART 的重建结果与720 个投影FBP 重建结果进一步处理后仅保留重建物体信息，定量计算区域如图3（g）虚线圆区域。在计算过程中，以720 个投影FBP 重建结果为参考图像，计算结果如表3 所示。从计算结果得出，用1/3 稀疏投影重建，PICCS 重建结果比SART 重建结果更加接近参考图像。

表3 720 个投影FBP 重建结果为参考图像的定量计算结果Table 3 Quantitative calculation results of 720 projection FBP reconstruction results as reference image

上述图像质量评价指标都需要参考图像，为了进一步分析重建结果，选取一个无参考图像评价指标信噪比（Signal to Noise Ratio，SNR）［13］，表达式如式（8）所示，GROI和SROI分别是图像中感兴趣区域的灰度均值和噪声的方差（感兴趣区域的方差），图像信噪比越高图像质量越好，噪声影响越小。为了比较1/3 稀疏投影 PICCS 和 SART 与 720 个投影 FBP 的重建结果质量，分别取图3（d）（e）（f）中 A 部分作为感兴趣区域，计算结果如表4 所示，SART 算法用240 个投影重建的结果受噪声影响较大，而PICCS 用240 个投影重建结果由于PICCS 算法引入高质量先验图像的约束抑制了噪声，噪声影响较小，重建图像质量较好。

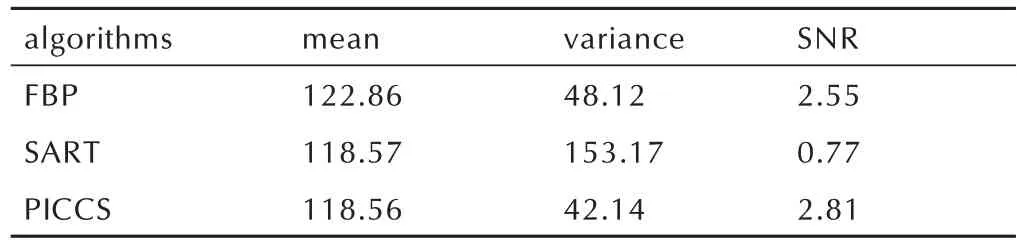
表4 SNR 计算结果（各算法感兴趣区域A）Table 4 SNR calculation results（region of interest A by different algorithms）

4 结论

（1）针对CT 检测PBX 效率低的问题，采用稀疏投影CT 扫描的方法，即通过减少投影采集数量提高检测效率。在稀疏投影CT 扫描重建实验中，通过采集1/3 稀疏的TATB 基PBX 的损伤试件投影进行图像重建，虽然迭代算法重建时间比FBP 长，但是随着计算机硬件的提升以及GPU 并行计算的出现，迭代重建时间会大大减少，本文方法检测效率还会进一步提升，所以本文最终检测效率提高2 倍左右。

（2）1/3 稀疏的PBX 投影是典型的不完备投影，本研究采用的PICCS 重建算法由于先验图像的约束，重建过程中能抑制噪声，减少伪影。实验结果表明，用1/3 稀疏的PBX 投影进行重建，与经典SART 重建算法相比，PICCS 重建算法可以重建出细小裂纹，重建结果与完备投影FBP 重建结果质量更加接近，满足对检测物体内部结构和缺陷的观察、判断。

（3）CT 广泛应用于PBX 缺陷检测以及细观内部呈现，所以对于稀疏投影CT 扫描重建实验中采集1/3稀疏投影检测效率提高2 倍左右，因研究内容以及精度要求不同而不同。