考虑T 应力的PBX裂纹尖端失效区和起裂行为

董天宝，袁洪魏，赵 龙，唐 维

（中国工程物理研究院化工材料研究所，四川 绵阳 621999）

1 引言

在武器系统中，高聚物粘结炸药（PBX）部件除了具备固有的爆轰性能外，常以承受载荷的结构件形式存在。在加工、装配、运输及服役过程中，PBX 部件在复杂受力状态下的结构完整与否，严重影响着武器系统使用的可靠性与安全性。复杂应力状态下PBX 裂纹起裂行为的研究，对其服役性能评估具有重要意义，而裂纹尖端失效区的描述是该行为研究和起裂准则建立的基础和前提。

小范围屈服下线弹性断裂力学认为，在裂纹尖端核心区域存在一定的屈服区，屈服区内材料发生屈服失效，屈服区外材料依然满足线弹性断裂力学理论［1］。TATB 基PBX 在拉伸/压缩过程中存在一定的塑性变形［2］，但没有明显的屈服阶段，参考岩石等材料研究领域中临界裂纹区（fracture processing zone）和微破裂区描述方法［3］，可以认为PBX 裂尖存在一个失效区域，在该失效区内PBX 材料发生力学失效，在失效区外材料依然满足PBX 弹塑性力学特性描述。美国阿拉莫斯实验室的 Liu C 等［4］对 PBX-9502 裂纹尖端区域应变场的进行监测，根据PBX-9502 拉伸破坏应变（0.2%～0.3%）推断出裂纹尖端附近存在较大的损伤区（damage zone），或 称 断 裂 过 程 区（fracture processing zone）。刘晨等［5］针对具有明显塑性特征的 TATB 基PBX，测量了裂纹尖端区域全场应变，数据表明PBX 裂纹尖端区域发生了塑性变形，存在裂纹尖端塑性区（crack tip plastic zone）。强洪夫等［6-7］基于统一强度理论建立了适用于固体推进剂的复合型裂纹尖端塑性区模型，并成功应用于固体推进剂复合型裂纹起裂准则，裂纹尖端塑性区的描述对于起裂行为研究非常重要。王阳等［8］针对HTPB 推进剂复合型裂纹，利用数字图像相关法获得了复合型裂纹尖端全场变形，确定出了应变集中区域边界形状，描述了复合型裂纹尖端应变场特征。由于PBX 材料破坏应变很小，裂纹尖端失效区试验观测较为困难，尚未见描述裂纹尖端失效区形状和大小的试验报道。

PBX 力学行为表现出拉压不对称的特性［9］，建立裂纹尖端失效区理论模型时，需要充分考虑材料的力学特性。PBX 裂纹尖端失效区计算准确与否依赖于强度准则的选取和裂纹尖端应力场的描述，根据以往的强度准则在PBX 结构破坏失效分析适用性研究［10-12］，以及文献［13］中不同强度准则下裂纹尖端失效区对比分析，认为Drucker-Prager 准则综合考虑了拉压比、静水压力和偏应力对材料强度的影响，更适合于PBX裂纹尖端失效区理论模型的建立。另一方面，以往的裂纹尖端失效区理论模型的建立过程中，往往只运用了裂纹尖端应力场中r-1/2奇异应力项［14］，而将T应力（非奇异的常数项）忽略。近年来研究表明，T应力对裂尖塑性区有着非常重要的影响［15-17］，越来越多的考虑T应力的起裂判据更加符合试验结果［18-19］。

PBX 结构件在武器系统中处于复杂应力状态，其裂纹起裂行为多呈现出复合型裂纹起裂特征。本研究以无限大平板中心贯穿斜裂纹为模型，基于Drucker-Prager 强度准则，建立考虑T应力的PBX 裂纹尖端失效区理论模型，利用裂纹尖端失效区最小半径开裂准则，研究裂纹倾角、裂纹面闭合摩擦以及T应力对PBX 裂纹裂尖失效区和起裂行为的影响，为复杂应力状态下PBX 结构裂纹起裂机理研究提供基础。

2 理论模型

2.1 复合型裂纹尖端附近应力场

Williams［14］指出裂纹尖端的弹性应力场可表述为：

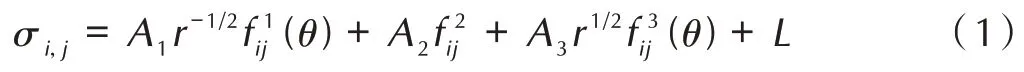
式中，第一项为奇异应力项，在裂纹尖端占据主导地位；第二项为非奇异常数项，即T应力。第三项及后续项为r的高阶项，当r→ 0 时，可以忽略不计。对于无限大平板含长度2a的中心贯穿斜裂纹模型，如图1 所示，其中σx和σy分别是x和y方向的远场应力，τxy为远场的剪应力。如果σx=σy，则裂纹尖端应力场为［19］：

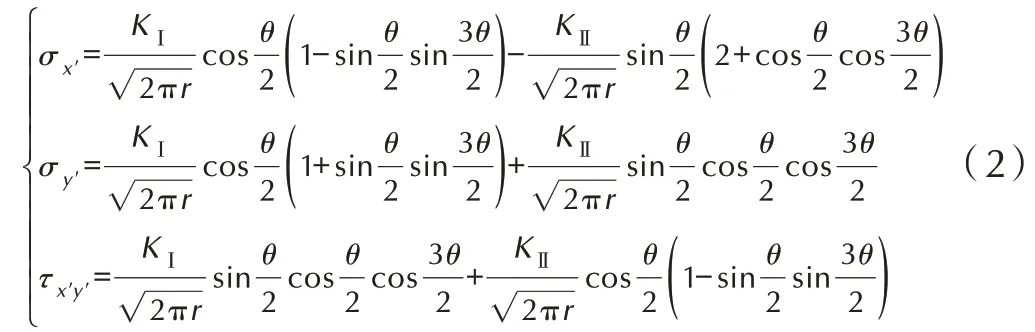
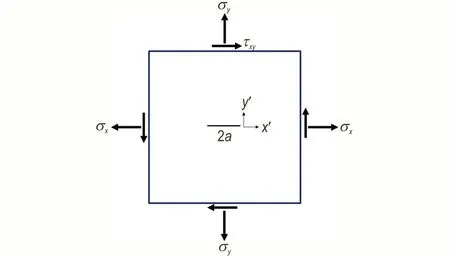
图1 含中心裂纹无限大平板Fig.1 An infinite plate with a central crack

式中，T和N所产生的应力统称为T应力。若图1 中裂纹为倾斜裂纹，则需要将远场应力分解为沿着裂纹和垂直于裂纹面方向的应力分量。本文主要研究远场单向拉伸压缩载荷下，无限大平板中心贯穿Ⅰ-Ⅱ复合型裂纹尖端失效区和起裂行为。在远场单向正应力加载下，其应力分解如图2 所示。局部坐标系x'-y'中应力分量为：

式中，β为裂纹与远场载荷之间的夹角，σ为远场单向拉伸或压缩应力。

图2 含中心裂纹无限大平板应力分解Fig.2 Stress analysis of an infinite plate with a central crack

远场拉伸（σ＞0）时，此时复合型裂纹Ⅰ型与Ⅱ型应力强度因子分量（KⅠ、KⅡ）和T应力［20］（T、N）的表达式如下：

远场压缩（σ＜0）时，裂纹两个表面相互接触，此时应力强度因子I型分量KⅠ= 0，同时考虑裂纹面闭合的摩擦效应。计算应力强度因子II型分量（KⅡ）时应使用有效剪切应力τeff［20］，图2中单向压缩条件下有效剪切应力τeff表达式为：

式中，μ为摩擦系数。此时，复合型裂纹的KⅠ、KⅡ、T、N表达式如下：

以上式（5）和式（7）中，KⅠ(β)、KⅡ(β)、T(β)和N(β)代表裂纹应力强度因子和T应力的无量纲参量，一定程度上代表着应力强度因子和T应力随β的变化情况。

2.2 强度准则的非主应力表达

选取Drucker-Prager 强度准则建立PBX Ⅰ-Ⅱ复合型裂纹尖端失效区理论模型，Drucker-Prager 强度准则主应力表达式如下［13］：

式中，σ1、σ2和σ3分别为第一、第二和第三主应力。材料破坏强度拉压比为α=σt/σc，σt和σc分别为材料单轴拉伸和压缩破坏强度。根据材料力学中主应力公式将式（8）转换为非主应力表达，平面应力状态为：

平面应变状态为：

2.3 考虑T应力的复合型裂纹尖端失效区

定义无限大板载荷应力水平为S=σ/σt，裂纹尖端失效区无量纲矢径为r/a，将引入T应力的裂纹尖端应力场表达式（3）代入式（9）和（10）中，得到平面应力状态下，包含裂纹尖端失效区无量纲矢径（r/a）的隐式控制方程为：

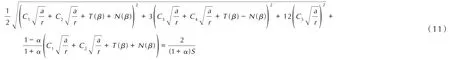
平面应变状态下，包含该无量纲矢径（r/a）的隐式控制方程为：

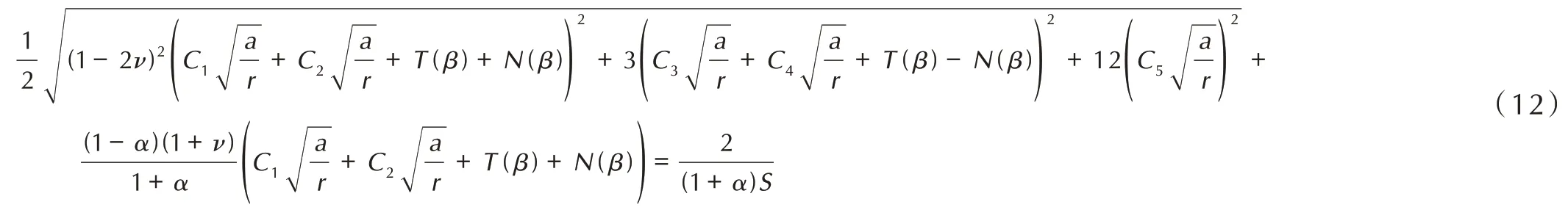
式（11）和式（12）中，C1，C2，C3，C4，C5表达式分别为：

求解上述隐式方程（11）和（12），即可获得复合型裂纹尖端失效区无量纲矢径（r/a）。当T= 0，N= 0时，无量纲矢径（r/a）的隐式方程可以退化为不考虑T应力的复合型裂纹尖端失效区显式表达式。

2.4 最小失效区半径起裂准则(r/a)min

复合型裂纹的起裂参数一般包括起裂角度和起裂强度。为了基于裂纹尖端失效区理论模型研究复合型裂纹起裂行为，引入最小失效区半径起裂准则［21-22］，假设裂纹沿着失效区半径最小的方向扩展，即：

以最小失效区半径(r/a)min表征起裂强度，对应角度θ0表征复合型裂纹起裂角，描述复合型裂纹的起裂行为。

3 结果与讨论

3.1 裂纹倾角β和应力水平S对裂纹参数的影响

图3给出了复合型裂纹尖端无量纲参数KⅠ（β）、KⅡ（β）、T（β）和N（β）随裂纹倾角β的变化情况。远场拉伸状态下，随着β的增大，沿着裂纹面方向T应力无量纲参数T（β）不断减小，垂直于裂纹面的压力恒为零。远场压缩状态下，裂纹面闭合仅存在应力强度因子Ⅱ型分量，处于纯Ⅱ型裂纹状态。随着β不断增大，裂纹尖端应力强度因子KII的无量纲参数KⅡ（β）先增大后减小。对于β＞arccot（μ）情况，裂纹尖端应力强度因子KⅡ恒为零。从公式（5）和公式（7）可以看出，复合型裂纹尖端KⅠ、KⅡ、T、N均与远场应力σ成简单线性关系。本研究以某TATB 基PBX 为例，计算PBX 材料复合型裂纹尖端失效区及起裂行为，材料参数见表1。

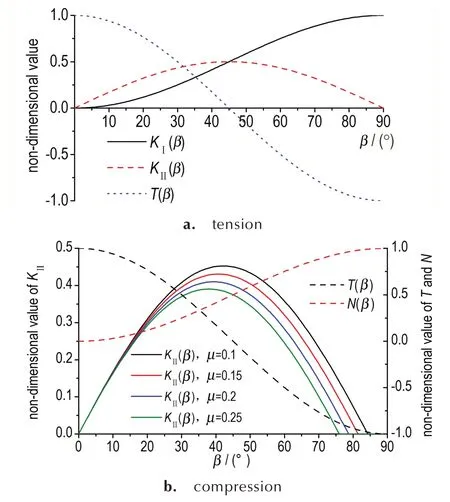
图3 远场拉伸和压缩下裂纹尖端无量纲参数随β 变化情况Fig.3 Non-dimensional value of crack tip parameters with different β under far field tension and compression

表1 TATB 基PBX 裂尖失效区计算参数Table 1 Calculation parameters for crack tip failure zone of PBX

3.2 T应力对裂尖失效区的影响

3.2.1 远场拉伸（σ＞0）

远场拉伸状态下，裂纹面张开无压力（N=0）。如图 4 所示，在应力水平不变（S=0.2）情况下，随着β的减小（90°→0°），裂纹由纯Ⅰ型，转变为Ⅰ-Ⅱ复合型，并趋向于Ⅱ型裂纹，裂纹尖端失效区尺寸显著减小；由于拉伸状态下，β从 0°变化到 90°过程中，T应力存在正负转换且对称。当β=45°时，T应力恒为零不影响失效区大小和形状；当β=90°时，T应力导致失效区显著减小；当β=22.5°时，T应力导致失效区显著增大。（注：全文图中 YES 表示考虑T应力，NO 表示不考虑T应力。）

图4 T 应力对不同倾角β 下PBXⅠ-Ⅱ复合型裂纹尖端失效区的影响Fig.4 Effects of T stress on PBX Ⅰ-Ⅱ mixed mode crack tip failure zone with different crack angle β（‘YES'and‘NO'represent that the T-stress is considered or not）

3.2.2 远场压缩（σ＜0）

远场压缩状态下，裂纹面闭合且存在一定的压力，此时裂纹面闭合摩擦效应不可忽略。T应力不仅包括沿着裂纹方向的T应力，还包括垂直于裂纹方向的N应力。裂纹尖端应力强度因子Ⅰ型分量KⅠ=0。应力强度因子Ⅱ型分量KⅡ取决于有效剪切应力τeff的大小。对于β＞arccot（μ）情况，裂纹尖端应力强度因子KⅡ=0。针对单向压缩比较容易破坏的裂纹倾角β=22.5°，研究T应力和裂纹面闭合摩擦对裂纹尖端失效区的影响。如图5 所示，T应力的引入，使裂纹尖端失效区显著减小。随着摩擦系数μ的增大，裂纹尖端失效区也显著减小。

3.3 T应力对起裂参数的影响

3.3.1 远场拉伸（σ＞0）

图5 T 应力对不同摩擦系数μ 下PBX 压剪裂纹尖端失效区的影响（β=22.5°）Fig.5 Effects of T stress on PBX compression-shear crack tip failure zone under different friction coefficient μ（β=22.5°）

图6 给出了远场拉伸下复合型裂纹起裂角度θ0和最小失效区半径（r/a）min随裂纹倾角β的变化情况。对于平面应力状态，由于考虑了材料拉压比α的影响，最小失效区半径准则与最大周向应力准则确定出的起裂角度有很大区别，如图6a 所示。随着拉压比的增大，（r/a）min准则确定出的起裂角明显增大，而σθmax准则确定出的起裂角与拉压比无关。对于（r/a）min准则来说，T应力使起裂角减小。图6b 中，随着材料拉压比的增大，失效区最小半径显著减小，复合型裂纹不易起裂。T应力使失效区最小半径显著增大（β＜45°）或减小（β＞45°），增加（β＜45°）降低（β＞45°）起裂风险。裂纹倾角β=90°时，失效区最小半径取得最大值，说明拉伸状态下最危险裂纹倾角β0=90°。

3.3.2 远场压缩（σ＜0）

图7 给出了远场压缩下纯Ⅱ型裂纹起裂角度θ0和最小失效区半径（r/a）min随裂纹倾角β的变化情况。远场压缩状态下，纯Ⅱ型裂纹面闭合，不仅需要考虑沿着裂纹方向T应力和垂直裂纹方向N应力的影响，还要考虑裂纹面闭合摩擦的影响。传统的σθmax准则无法区分平面应力和平面应变问题，而（r/a）min准则计算表明，平面应变比平面应力状态起裂角更大一些，如图7 所示；T应力使起裂角增大，而且这种增大趋势在β偏大且β＜arccot（μ）的时候更加明显；计算表明，摩擦系数不影响压缩纯Ⅱ型裂纹起裂角，仅在裂纹倾角β＞arccot（μ）下，摩擦效应使纯Ⅱ型裂纹应力强度因子为零，不产生裂尖失效区，裂纹压缩闭合“锁死”不发生起裂。

图6 起裂角度和最小失效区半径随β 变化曲线（平面应力）Fig.6 Fracture angles and minimum failure zone radius variation curves with β（plane stress）

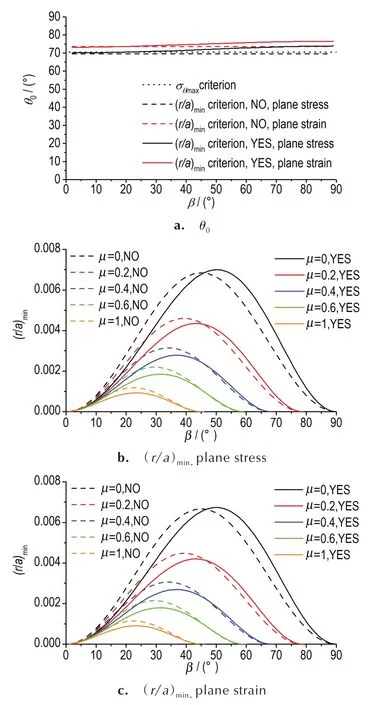
图7 起裂角度和最小失效区半径随β 变化曲线Fig.7 Fracture angle and minimum failure zone radius variation curves with β

图7b 和图7c 给出了不同摩擦系数μ下最小失效区半径随β的变化情况。随着摩擦系数的增大，最小失效区半径越来越小，纯Ⅱ型愈加不易起裂；最小失效区半径（r/a）min随裂纹倾角变化存在极大值，说明存在最危险裂纹倾角β0，而且T应力使危险裂纹倾角β0增大。

图8 危险裂纹倾角β0和（r/a）min随摩擦系数变化曲线Fig.8 Danger crack angles β0 and（r/a）min variation curves with friction coefficient μ

进一步统计图7 中不同摩擦系数下的（r/a）min的极大值点，即危险裂纹倾角β0和对应的最小失效区半径（r/a）min极值点，结果如图 8 所示。经典理论认为［1］，对于远场压缩下无限大平板中心贯穿斜裂纹模型，最危险裂纹倾角β0=0.5arccot（μ），不考虑T应力的（r/a）min准则计算出的危险裂纹倾角β0与经典理论解一致，T应力和摩擦效应均使危险裂纹倾角β0显著增大，随着摩擦系数的增大，T应力对裂纹倾角β0增大效果越来越不明显。T应力减小了失效区最小半径，裂纹相对不易起裂。

4 结论

以含中心贯穿斜裂纹无限大平板为模型，基于引入T应力的裂纹尖端应力场和Drucker-Prager 强度准则，建立了考虑T应力的PBX 裂纹尖端失效区理论模型，计算T应力对PBX 裂纹尖端失效区的形状和大小的影响，基于裂纹尖端失效区最小半径起裂准则，分析了T应力对裂纹起裂行为的影响。

（1）远场拉伸下，裂纹倾角β减小过程中（90°→0°），裂纹由纯Ⅰ型转变为Ⅰ-Ⅱ复合型，并趋向于Ⅱ型裂纹，裂尖失效区尺寸显著减小。当β=45°时，T应力恒为零不影响失效区大小和形状；当β＜45°时，T应力导致失效区显著增大；当β＞45°时，T应力导致失效区显著减小。

（2）远场拉伸下，考虑T应力的（r/a）min准则与传统σθmax准则对PBX 裂纹起裂行为的描述有显著区别。随着拉压比的增大，（r/a）min准则确定出的起裂角明显增大，失效区最小半径明显减小，裂纹不易起裂。T应力使起裂角减小。β＜45°时，T应力使裂纹容易发生起裂。β＞45°时，T应力使裂纹不易起裂。

（3）远场压缩下，对于β=22.5°，T应力使裂纹尖端失效区明显减小。随着摩擦系数的增大，裂纹尖端失效区显著减小。

（4）远场压缩下，传统σθmax准则和（r/a）min准则确定出起裂角分别为70.5°和69.6°（平面应力）、73.6°（平面应变）。在β＜arccot（μ）范围内，裂纹面闭合摩擦不影响起裂角大小，随着β的增大，T应力使起裂角不断增大。失效区最小半径随摩擦系数增大而减小，摩擦效应使裂纹不易起裂。（r/a）min准则与传统理论计算得到的最危险裂纹倾角β0一致，T应力使危险裂纹倾角显著增大，T应力减小了失效区最小半径，降低了起裂风险。