起伏管道内水流冲击滞留气团的三维动态特性模拟

卢坤铭，周领*，曹波，刘德有，王欢

(1. 河海大学水利水电学院，江苏 南京 210098； 2. 国网新源水电有限公司新安江水力发电厂， 浙江 建德 311600)

在实际输水系统中，管道布置常因地理条件限制及工程需要而呈现高低起伏状态.在这类管道系统中，气团极易滞留于管道顶部，当系统启动(阀门、水泵开启)时，有压水流将冲击滞留气团而产生瞬变流，从而易产生异常的危险压力，极有可能造成管道爆裂，危害整个管道系统的安全运行[1-2].

目前，针对水流冲击滞留气团瞬变流现象，现有的模型大多为一维数学模型.作为该问题研究的先驱者，MARTIN[3]基于刚性水体理论，首次对水流冲击滞留气团的现象进行了研究，指出滞留气团的存在可能引起异常的压力波动.ZHOU等[4]对MARTIN的刚性模型进行了改进，充分考虑了冲击水体长度的动态变化.CHAIKO等[5]考虑水体和管道的弹性，建立了3种弹性数学模型，并给出了各弹性模型的适用范围.一些学者先后提出了一维“虚拟塞”“刚性塞”数学模型，与考虑全水体弹性数学模型相比，成功地避免了特征线法在水气交界面动态追踪时的复杂插值处理，并保持了同样的计算精度；指出在气团含量很小的情况下，刚性水体模型并不适用[6-8].随后，ZHOU等[9]通过试验和一维数值模拟，研究了2段滞留气团和阻断水体之间的关系，结果表明：与单个气团相比，2个滞留气团可能导致更加危险的峰值压力，这与2个气团的大小及阻断水体长度密切相关.然而，有些学者的研究成果表明现有一维数学模型常常低估了气团压力峰值，这与一维模型的基本假定有关，包括：① 滞留气团占据整个管道截面，水气交界面与管中心线垂直，气、水互不掺混；② 在稳态和瞬态情况下，管道内的水流阻力特性不变；③ 管道内滞留气团假定为完善气体，满足气体热力学多变过程方程[4,6-9].但试验观测发现，水-气耦合过程呈现明显的三维特征，整个瞬变过程中水-气交界面自由变化，会出现气团分离成2个或若干个气团的情况，能量衰减加快，这将导致数学模型的计算结果与试验有所偏差.

为了能精细模拟水气耦合过程，近年来，论文作者研究团队成功将计算流体动力学(CFD)方法引入对简单管道内含滞留气团瞬变流进行了二维、三维数值模拟，并通过试验数据验证CFD方法的可行性和准确性[10-11].水平管道情况模拟结果显示，不同湍流模型对滞留气团瞬态特性和压力变化有较大影响[12]；同时，通过三维模拟手段揭示了竖直管道内水流冲击滞留气团瞬态过程中滞留气团的热力学特性.此外，MARTINS等[13]采用同样的三维CFD方法研究了管道填充过程中滞留气团的运动特性，指出三维模拟能更好地揭示水气动态变化特性.

文中将采用三维CFD方法模拟起伏管道内水流冲击滞留气团的瞬变流.现有的一维模型存在诸多假定，且计算结果与试验差别较大，很难采用一维模型来对该瞬变流进行深入的研究.对于水-气耦合三维瞬变流，试验手段很难准确、全面记录水-气的三维动态特性.三维CFD方法已被证实可用于简单管道瞬变问题的研究，然而，起伏管道的情况更为复杂，需要进一步研究.文中将对比分析3种湍流模型(Standardk-ε、RNGk-ε和Realizablek-ε)对结果的影响，并将三维计算结果、一维计算结果和试验结果进行对比；同时，研究瞬变过程中气团压力波动和气水形态变化.

1 试验研究

针对起伏管道内水流冲击滞留气团的瞬变流现象，设计搭建了如图1所示的试验系统，分析多个滞留气团的相互作用规律[7].整个系统主要由潜水泵、气压罐、电磁流量计、球阀、管道、空气阀、排水阀等组成.整个管道总长10.97 m，由内径D为4 cm的透明有机玻璃管道(长9.883 m，壁厚e为1 cm)及钢管(长1.087 m，壁厚0.5 cm)组成.起伏段采用透明的有机玻璃，以便于观察水-气交界面的变化及水-气两相分布规律.进气孔直径3.2 mm，排水阀直径4.2 mm.图1中给出了管道弯曲段最高点和最低点处的沿线长度x和高程位置z.管道上安装了1个球阀及8个压力传感器(PT1, PT2, PT3, PT4, PT5, PT6, PT7, PT8)，其安装位置见表1.

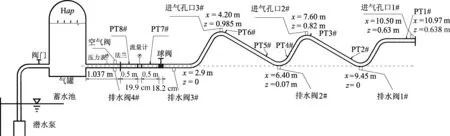
图1 试验装置布置图

Fig.1 Test equipment arrangement diagram

气压罐直径0.75 m，高2.075 m，有效容积750 L，可以提供0～1 MPa的基本恒定的水压力.电磁流量计用于测量水流量，其流量范围为0～25 m3/h；压力表的最大量程为1 MPa，用于读取压力罐的压力值；压力传感器的测量范围为0～5 MPa，以测量不同位置处的压力值；数据采集系统将相应的电压信号转换为压力和流量值，文中采集频率为1 000 Hz.

表1 球阀及压力传感器位置

文中将针对起伏管道内初始单个滞留气团的瞬变过程进行三维模拟，模拟工况参数见表2，表中pr，xf，xu，La0分别为入口压力、初始冲击水体下游断面位置、阻断水体上游断面位置、气团长度.初始时所有阀门关闭，球阀快速开启以实现水流冲击气团瞬变过程，球阀开启时间0.1 s.

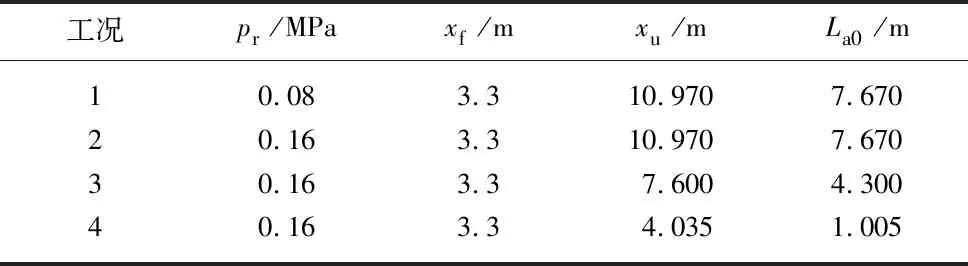
表2 模拟工况参数

2 数值模型

2.1 基本控制方程

采用VOF模型[14]追踪水气交界面，三维模型的基本控制方程[10, 15]如下.

容积比率方程为

(1)

动量方程为

(2)

能量方程为

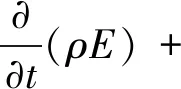
(3)

式中:ρw为水体密度；αw为水体体积分数；t为时间；v为流体速度；ρ为水-气混合物密度；p为静压；μ为水-气混合物黏度；μw，μa分别为水、气相流体黏度；g为重力加速度；F为外部体积力；E为总能；T为温度；keff为有效传热系数.

模拟中，气体、水体均可压.假定气体遵循理想气体定律，水体状态方程为

(4)

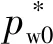
2.2 湍流模型

文中对比了Standardk-ε、RNGk-ε、Realizablek-ε这3种湍流模型计算结果.3种模型都适用于湍流，分子之间的黏性可以忽略，区别在于计算湍流黏性的方法不同，`以及湍流的产生和扩散的因素不同.

2.3 离散格式

采用的离散方法为有限体积法(FVM)，速度、压力和密度的耦合方法选择PISO算法，压力项采用PRESTO格式，动量项、能量项采用二阶迎风格式，湍动能项、湍流耗散项采用一阶迎风格式，体积分数采用Geo-Reconstruct格式进行离散，时间差分采用一阶隐式格式，时间步长为0.000 1 s，计算时长为5 s.

2.4 几何模型及边界条件

图2为3D模拟计算域及网格分布图.计算域中所有网格采用六面体结构化网格.

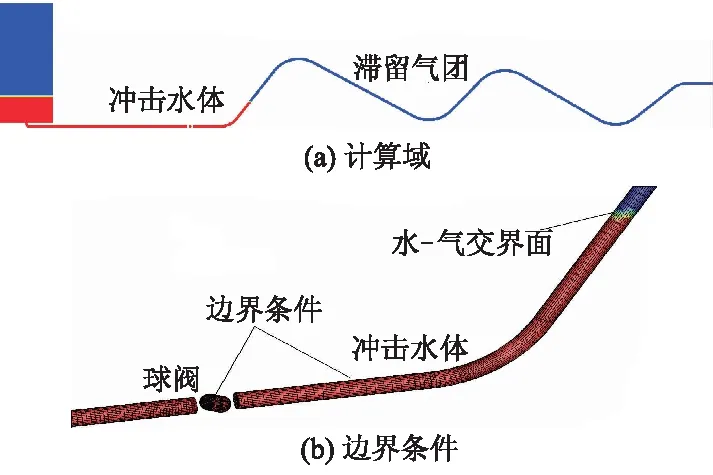
图2 计算域及网格分布

3 结果与分析

3.1 网格无关性分析

采用3套网格针对工况1进行对比分析.表3为网格信息，表中n，T，ε分别为网格数量、计算时间、最大压力误差.图3为压力计算与试验结果.随着网格数的增加，计算耗时显著延长，系统最大压力的精度有所提升，而3种网格下计算的压力变化曲线的区别并不明显.考虑到计算效率，最终采用第1套网格来进行相关模拟分析.

表3 网格信息

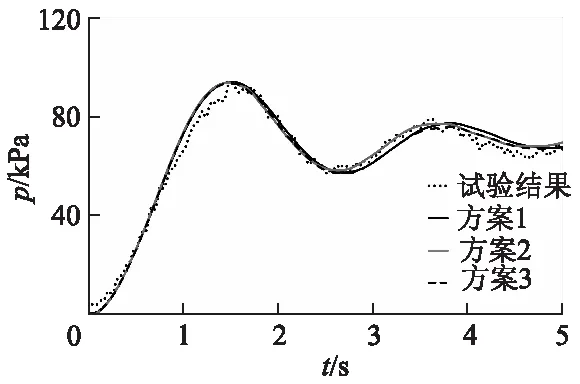
图3 压力计算与试验结果

3.2 湍流模型的影响

图4为工况1及工况2时，不同湍流模型下，压力波动计算结果与试验的对比结果.可以看出：① 对工况1(pr=0.08 MPa)，压力幅值大小、波动周期都与试验数据十分吻合，3种湍流模型都有效地模拟了气团压力变化过程.对于第1压力峰值，Standardk-ε湍流模型的结果略高于试验值，误差为0.7%，RNGk-ε湍流模型的结果略低于试验值，误差为-0.2%；Realizablek-ε模型与试验结果的误差最大，为4.8%.在第2压力峰值处，RNGk-ε,Realizablek-ε这2种湍流模型与试验结果的误差较大，其原因为在较低入口压力下，在近壁面区湍流的发展并不充分，使考虑了高应变率和旋流的修正模型产生了较大的偏差.对时间响应，Standardk-ε湍流模型的时间响应与试验结果几乎同步，而2种修正模型则略早于试验结果.② 对工况2(pr=0.16 MPa)，对于第1压力峰值，Standardk-ε湍流模型的结果与试验非常吻合，误差仅为0.1%.而另外2种湍流模型的误差则较大，分别为4.7%和9.0%，可能的原因是在较高压入口压力下，整个系统湍流充分发展，能量损耗主要以水体与管壁的热传导，以及水-气的热交换为主，修正模型的湍动黏度计算则考虑了流动中的旋流和曲率的影响.对于时间响应，该工况与pr=0.08 MPa工况存在相似的规律.此外，工况3,4可得类似结论，由于篇幅限制，在此不再赘述.

图4 不同湍流模型下，PT1#处压力计算结果与试验结果对比

Fig.4 Comparisons between calculated and experimental results of pressure at PT1# with different turbulence models

3.3 现有一维模型计算结果

图5为4种试验工况下，采用Standardk-ε湍流模型三维模拟得出的压力波动曲线.与现有一维模型计算结果、试验观测数据的对比结果.其中，一维模型是采用本课题组已发表的弹性水体数学模型[10]；管道恒定摩阻取f=0.1.

结果显示，与一维模型相比，三维CFD计算瞬变压力结果与试验结果更为接近.

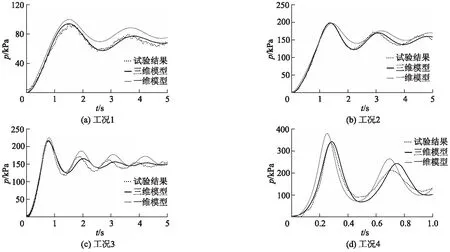
图5 计算结果与试验结果对比

3.4 三维模拟误差分析

工况1和工况2时，三维CFD方法能较为准确地预测出瞬变压力，如图5所示.然而，对于初始气团较短的工况3，4，虽然三维CFD计算结果明显好于一维模型结果，但与试验结果仍有差别.可能的原因是，随着气团初始长度减小，水气耦合变得更加剧烈，如工况4的压力峰值和波动频率远高于工况2，这意味着水气掺混的程度更加剧烈，将涉及复杂的热力学问题.另外，试验发现，工况4中，压力峰值较大，出现轻微的管道振动.然而，文中三维模拟没有考虑水-气-管壁复杂的热传递和热交换问题，以及流固耦合现象.另外，数值模拟很难准确设定和考虑实际管道材料、流体特性等.

3.5 水-气动态特性

图6为工况2(已证实该工况下，三维计算结果的准确性)下水-气两相分布变化云图.

图6 不同时刻水-气动态特性

结合图5b，起伏管道内水流冲击滞留气团过程中，水-气三维动态特性如下：

1)t=0 s, 初始时刻，上游管道、阀门处都充满了有压水体，冲击水体至起伏管道末端为气体，压强为大气压力，水-气交界面位于6#管道处，且几乎垂直于管道中心线.

2)t=0.30 s，迅速打开阀门后，在有压水流的快速冲击下，滞留气团首次被压缩，其压力迅速增大，水-气交界面在1.5 s内沿管道迅速运动至4#和3#管道的弯曲处.水体和滞留气团的交界面十分明显，但由于重力的作用，很明显没有垂直于管道中心线.

3)t为0.30～0.60 s时，冲击水体从6#管道运动至6#和5#管道的弯曲处，在重力的作用下，管道下方的水体运动速度更快，比管道上方的水体提前到达5#和4#管道的弯曲处，气团由于密度小被冲击水体挤压在管道的上方，水-气交界面扩大为“楔形”，与管中心线大致呈-45°夹角，面积逐渐增大.

4)t=0.95 s，在高速水流的冲击作用下，5#和4#管道的弯曲处填充了大量水体，滞留气团继续被压缩，但存在少部分的气团被分离出来，水-气互相掺混，部分气体溶解在水体中，形成气泡流存在管道弯曲处.在滞留气团的阻力影响以及重力作用下，管道下方的水体运动速度减慢，但仍大于管道上方的水体运动速度，导致水-气交界面继续以“楔形”存在，与管道中心线的夹角为45°.相比于t=0.6 s，滞留气团的压力继续增大，对水体的缓冲作用逐渐增强，导致水-气交界面的面积明显减小.

5)t=1.60 s，气团开始膨胀，扩大了水-气交界面的面积，由于惯性和重力作用，管道下方部分水体沿着3#管道运动至3#和2#管道的弯曲处，同时气团压力开始减小.

6)t=2.15 s，随着气团压力达到最小值，滞留气团的体积膨胀至最大，水体回流至4#管道，水-气交界面垂直于管道中心线.

4 结 论

1) 针对起伏管道内水流冲击滞留气团的瞬变流现象，所采用的三维CFD模型能够有效模拟瞬变过程中压力波动、气-水界面变化，且与试验结果吻合较好.三维CFD方法可以对整个流场实现可视化处理，这是试验及一维模型都难以达到的.

2) 湍流模型是三维CFD建模的核心部分之一，影响管路系统的阻力、能量衰减的核心因素.对比发现，Standardk-ε湍流模型能够更好地模拟起伏管道内水流冲击滞留气团瞬变过程的压力峰值和波动周期.

3) 三维CFD模拟结果与试验观察结果显示，随着气团的压缩和膨胀，水-气两相互相掺混，交界面并不垂直于管道中心线，而是与管道中心线呈一定的夹角，水-气交界面自由变化，以及水气掺混等复杂两相流态.

4) 与一维模型相比，三维CFD计算结果与试验结果更为接近.一维模型存在较大计算误差，是因为其本身假定造成的，这些假定均与实际情况有较大差别.

5) 对于初始气团较短的情况，三维CFD计算结果明显好于一维模型结果，但与试验结果仍有差别.原因可能是，随着气团初始长度减小，水气耦合、水气掺混的程度更加剧烈，涉及复杂的热力学问题.