依据响应曲面法和BP神经网络对木纤维脉冲-旋流气流干燥工艺优化1)

许靖 迟祥 陈献明 程万里

(东北林业大学，哈尔滨,150040)

木质纤维干燥是生产中的重要环节，它与生产过程中的能源消耗和产品质量密切相关[1-3]。木质纤维的常用干燥方式主要有滚筒干燥、喷雾干燥、气流干燥和流化床干燥等，其干燥时间相对较长、能耗较高，干燥过程中纤维不能良好地分散，造成纤维过干或过湿；干燥的纤维冗絮结团、设备易发生堵塞，高温易着火[4-7]等。目前常规单级纤维干燥设备难以适用现代干燥的需求，众多干燥设备制造企业采用组合式干燥方法对粉体干燥开展研究和设备研发[8]。汪智国等[9]开发出一种新型高效的气流-旋流组合干燥方式，与传统Hoechst干燥系统相比，设备投资成本和能耗降低，干燥效率大幅提高。林金娜[10]采用对撞流干燥方法研究了竹纤维干燥对竹塑复合材料性能影响，结果表明对撞流干燥方式干燥竹纤维浆料，提高了干燥过程的传热传质效果，纤维质量得到保证条件下应尽可能使用较高的干燥气流速度。胡学功等[11]就垂直对撞流干燥机的干燥特性开展了实验研究和理论分析，研究得到了物料在对撞腔中的停留规律，发现物料再循环的干燥效果最佳。Doymaz[12]在强制对流热空气干燥器中研究物料的水分移动规律，通过应用Fick的扩散模型描述了切片的水分转移，证明干燥发生在速率下降期。

脉冲-旋流气流干燥装置是由多级干燥机相互串联构成的干燥系统，装置通过热交换器加热形成高温气体，在压力作用下流动，组合脉冲气流干燥器和旋流干燥器，发挥其各自的优势快速高效达到干燥目的。此装置可以在8～20 s的短时间内结束对湿木质纤维的干燥，传质效率高；相关研究对能耗成本核算表明，其所需能耗成本大约是常规烘箱干燥的50%；物料悬浮流动过程中，颗粒小的木质纤维在干燥器中的停息时间短，颗粒较大的木质纤维停息时间长，因此物料干燥均匀，很难遇到局部过干现象[13-14]。

杨木纤维在脉冲-旋流气流干燥装置干燥过程中，初含水率、进风温度、进风速度和进料速度对杨木纤维终含水率都有一定影响。为了快速高效获得稳定在1%～3%含水率的杨木纤维，需要对工艺参数进行优化。为探讨脉冲-旋流气流干燥工艺对木质纤维终含水率的影响，笔者采用(Design-Expert)软件设计试验，考查影响木质纤维干燥质量的因素，并确定主控因素；选用BP神经网络方法完成终含水率预测模型的构建，确定脉冲-旋流气流干燥设备工艺参数与其终含水率的映射关系，以期为丰富木质纤维气流干燥理论体系及其工业化应用提供技术支持和理论依据。

1 材料与方法

1.1 材料与设备

速生中汉杨17(P.deltoidsBartr. CL.‘zhonghan 17’)废弃碎单板，由哈尔滨市永旭实业人造板公司提供。将速生杨木碎单板通过纤维粉碎机(MF-600干法生物质纤维粉碎机，由江苏富阳机械有限公司设计制造)粉碎加工，制备60～80目的杨木纤维；MQG-50脉冲-旋流气流干燥装置，由常州健达干燥设备有限公司生产。

1.2 响应曲面试验设计

本试验选用Design-Expert软件设计4因素3水平Box-Behnken实验，因素水平见表1。其中，废弃碎单板初含水率不等，因素A取碎单板平均初含水率51.6%、平均气干含水率12.4%和中间值32.0%，因素B、C和D依据前期研究结果设定[14]。

表1 响应面试验设计因素水平

试验中考查初含水率、进风温度、进料速度和进风速度对杨木纤维终含水率的影响。Box-Behnken实验方案设计结果为全部实验总计29组，其中中心点设置为5组重复实验。29组杨木纤维干燥终含水率平均值为4.0%，最大值为7.8%，最小值为1.0%。

1.3 含水率预测模型的构建

BP神经网络是机器学习的一条分支，其学习规则是通过更迭神经元之间的连接权值来减少系统实际输出和期望输出的误差以达到精确要求[15-16]。BP神经网络通过自我学习，自动调整自变量和因变量间庞杂的映射关系，因此可以考虑将这种建模方法应用在各类用于预测数值型数据的回归问题上。

本研究经由TensorFlow框架选用python编程语言建构BP神经网络。根据实际工艺流程涉及到的工艺参数，采用3层BP神经网络结构，输入层节点设置为4，输出层节点设置为1。关于隐藏层节点数的确定，通过经验公式(1)，根据拟合结果适当调整，经过反复试验，将隐藏层节点数设置为10。隐藏层经验公式：

(1)

式中：Lhid为隐藏层节点数；Lin为输入层节点数；Lout为输出层节点数。

利用响应曲面法得到的样本数据共29组，抽取其中21组作为训练数据，8组作为测试数据构造第一个神经网络。运用数据建立模型前，为了加快神经网络梯度下降求最优解的速度和精度，对所有样本数据进行归一化处理，将所有数据范围压缩在0～1范围内。模型建构完毕，进行反归一化操作。扩充样本数据至92组，抽取69组训练网络，23组作为测试构造第二个神经网络。Min-Max Normalization归一化公式：

(2)

式中：y为归一化后结果值；xi为归一化前样本数据值；xmin为样本数据中最小值；xmax为样本数据中最大值。

选择Sigmoid函数激活隐藏层，神经网络利用梯度下降算法优化对象，学习效率设置为0.01，最大迭代步数设置为200 000，选择皮尔森相关系数反映实际输出和期望输出的相关度。图1所示为BP神经网络结构，皮尔森相关系数公式：

(3)

式中：r为皮尔森相关系数；xtest为测试数据实测值；ypred为期望输出预测值；N为数据总量。

2 结果与分析

2.1 响应曲面法试验结果

通过Design-Expert软件对试验数据进行方程回归分析，以初含水率(A)、进风温度(B)、进料速度(C)和进风速度(D)为自变量，杨木纤维终含水率(Y)为响应值，拟合得到的响应曲面的二次回归方程为：

Y=4.40+1.95A-1.35B+1.13C+0.17D-0.40AB+0.40AC+0.30AD-0.15BC+0BD+0.050CD-0.54A2+0.11B2-

0.092C2-0.44D2。

(4)

图1 杨木纤维干燥预测的BP神经网络结构

Analysis模块下挑选ANOVA解析，可以获得方差分析表及回归方程。结果列于表2。

在方差分析中，通常将P<0.05视为显著，P<0.01为极显著。表3模型F值为71.86和极低的P值意味着模型是极显著的，4个影响因素中有3个是显著因素，显著程度从大到小顺序为初含水率、进风温度、进料速度、进风速度。分析结果中决定系数R2值是0.986 3，校正决定系数值等于0.972 6，意味着杨木纤维干燥试验值与预测值间有较好的一致性，试验误差较小。本模型中0.58的失拟值相对纯误差是不明显的，数值较低的失拟值反映出模型占据更好的适合度。

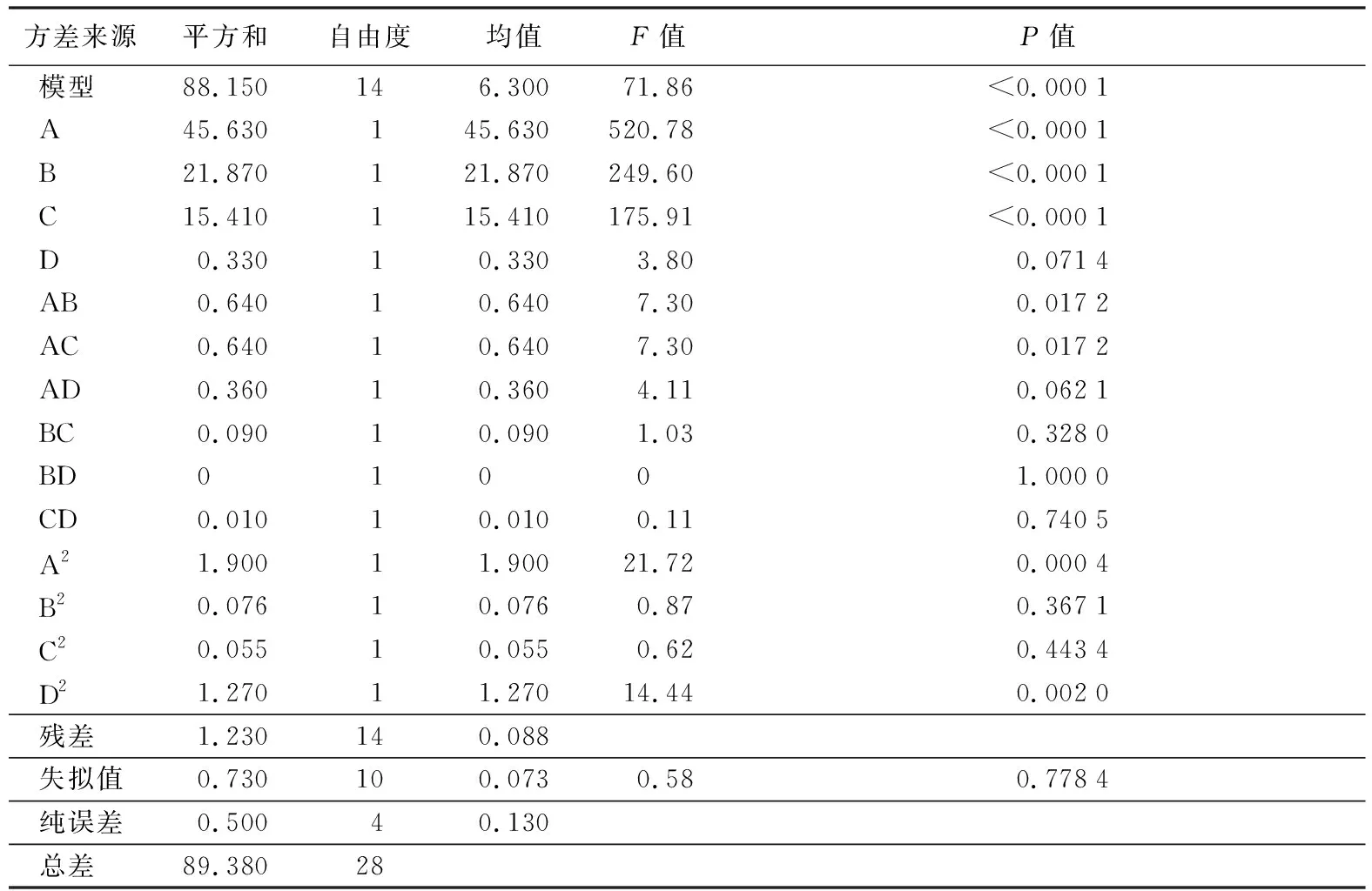
表2 多元回归模型方差分析表

Analysis模块下的Model Graphs选项，选择能清晰知晓各自变量与响应值之间关系的响应曲面和等高线图，如图2—图4。

图2 初含水率和进风温度交互影响杨木纤维终含水率的响应曲面和等高线图

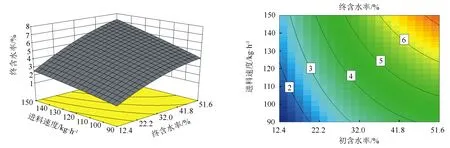
图3 初含水率和进料速度交互影响杨木纤维终含水率的响应曲面和等高线图

图4 初含水率和进风速度交互影响杨木纤维终含水率的响应曲面和等高线图

图2所示，随着杨木纤维初含水率的降低及脉冲-旋流气流干燥装置进风温度的提高，杨木纤维终含水率有着极为显著的降低。原因是进风温度越高，形成较高的温度梯度差，纤维内部水分迁移到表面速度越快，纤维终含水率越低。纤维初含水率越低，实验条件不改变情况下干燥后得到的纤维终含水率越低。图3和图4显示，增大干燥装置进料速度会使纤维终含水率出现显著的增大，其原因是相同时间投入更多的物料，管道气流中水分提高，降低了纤维内部与表面的含水率梯度，水分迁移速度变慢，终含水率偏高[17-18]。进风速度由9 m/s上升到11 m/s时，杨木纤维在装置中停留时间短，终含水率提高。当进风速度由11 m/s上升到13 m/s时，终含水率反而呈下降趋势，分析原因可能是进风速度的增加导致杨木纤维部分出现断裂，纤维露在气流中的面积增大，传质速度增加，影响实验结果。相比其余3个影响因素，进风速度的提升使纤维终含水率先升高后下降的程度并不显著，呈现在响应曲面图上的凸起弧度并不直观。

利用Design-Expert软件Optimization模块功能限定杨木纤维终含水率为1%～3%，得到的优化方案是：木纤维初含水率32.0%时，进风温度240 ℃，进料速率120 kg/h、进风速度9 m/s，此条件终含水率预测值为2.55%；木纤维初含水率12.4%时，进风温度200 ℃，进料速率90 kg/h，进风速度11 m/s，此条件终含水率预测值为1.083%。进行验证试验，两种条件下杨木纤维实际终含水率分别是2.6%和1.0%，与预测值存在较好的一致性。

2.2 BP神经网络拟合结果

根据选定的29组样本数据，通过训练确立BP神经网络模型，调用Matplotlib绘图库功能获得训练拟合效果如图5所示。可以看出，神经网络在完成设定迭代步数后，期望输出曲线大部分矫正，基本与测试样本曲线趋势一致，计算得到的皮尔森相关系数为0.962 0，证明该模型具备较良好的预测能力和准确性，但结果依然有晋升空间。

图5 29组样本数据神经网络拟合效果图

扩充样本数据至92组，再次通过训练构建神经网络模型，得到的拟合效果图如图6所示。可以直观看到，随着训练损失值不断减小，初始迭代10 000步预期错误较大的数值最终回归到测试数据数值附近，除个别样本存在较大误差，模型的预测结果与真实值的偏差大部分被矫正，期望曲线更逼近测试曲线。相比图5，图6中曲线间完全重合的部分大幅增加，表明模型预测更为精准。程序运行结束，神经网络皮尔森相关系数数值为0.989 6。扩充样本数据数目使神经网络模型的精确度提高，原因是多容量样本数据可以充分反映出样本的特征，限定期望值转变的范围，从而改良了神经网络的训练结果。

2.3 响应曲面法和BP神经网络试验结果对比

将神经网络模型和响应曲面法试验结果比较，使用常见的回归分析评判指标均方根误差(ERMS)、决定系数(R2)和皮尔森相关系数作为模型评价标准。模型优化效果比较见表3，均方根误差(ERMS)和决定系数(R2)的计算公式：

(5)

(6)

图6 92组样本数据神经网络拟合效果图

表3 响应曲面法和神经网络预测结果对比

依据回归分析评判标准，决定系数(R2)越高，均方根误差(ERMS)越低，表明模型预测结果和实测值越匹配，建立的模型越准确。由表5可知，3组优化结果都精确地实现了对杨木纤维干燥的预测。相比之下，29组样本数据构建的神经网络模型预测相对较差，92组样本数据构建的神经网络模型预测准确度次之，响应曲面法预测偏差最小，模型预测准确度相对更好。考虑到BP神经网络使用梯度下降法优化目标函数所带来的收敛速度慢、响应时间长等问题，可以采取另一种选择，借用响应曲面法工具，通过有限次数的试验，分析确定相似的预测模型，指导后续的设计或实验。

3 结论

采用Box-Behnken设计方法进行响应曲面法试验，选取杨木纤维脉冲-旋流气流干燥过程中初含水率、进风温度、进料速度和进风速度4个因素作为自变量，以杨木纤维终含水率作为因变量建立响应曲面模型，通过方差分析，确定了影响杨木终含水率的因素，从大到小顺序为初含水率、进风温度、进料速度、进风速度。建构BP神经网络模型，迭代成果阐明，足够的样本数据反映出规律特征后，预测模型的优化效果得以改善。将响应曲面法和BP神经网络模型优化效果实行对照，响应曲面法的均方根误差低于神经网络模型，R2值比神经网络模型高，这表明响应曲面法的优化水平更好。最终可选用响应曲面法优化得到的优化工艺方案：木纤维初含水率32.0%时，进风温度240 ℃，进料速率120 kg/h，进风速度9 m/s，此条件终含水率为2.6%；木纤维初含水率12.4%时，进风温度200 ℃，进料速率90 kg/h，进风速度11 m/s，此条件下终含水率预测值为1.0%。本试验的两种优化方法具有可行性，研究结果可为丰富木质纤维气流干燥理论体系及其工业化应用提供技术支持和理论依据。