变精度极大相容块粗糙集模型及其属性约简*

孙 妍，米据生，冯 涛，李磊军，梁美社,3

1.河北师范大学 数学与信息科学学院，石家庄 050024

2.河北科技大学 理学院，石家庄 050018

3.石家庄职业技术学院 科技发展与校企合作部，石家庄 050081

1 引言

Pawlak 于1982 年提出了粗糙集理论[1]，该理论是知识发现和数据挖掘的重要工具，为处理不精确数据和不完全信息的问题提出了一个新的框架，已被广泛地应用于模式识别、人工智能以及智能信息处理等领域[2-4]。

经典Pawlak 粗糙集模型处理的信息系统都是完备的，在实际生活中由于各种因素，信息系统中的某些属性值可能出现缺失[5]，文献[6]对这种不完备的信息系统做出两种解释：一是“丢失”值，即该值被擦除或者没有被插入到数据集中；二是“不关心”值，理解为来自于该属性值域中的任意值。在通常的知识发现中，一般先对数据进行预处理，通过对数据分析，填补缺失的数据，或者从样本数据出发，通过某种训练算法，推算缺失数据[7]。

基于不完备信息系统的知识发现是目前研究的热点问题。近年来许多学者在经典粗糙集模型上进行扩展，对等价关系进行弱化，提出了基于相似关系、相容关系以及邻域关系等构造新模型的方法来解决不完备信息系统的问题[8-10]。文献[7]在不完备信息系统中提出了极大相容块的定义，利用极大相容块在只含有缺失值为“不关心”值的不完备信息系统上构造精度较高的上下近似，并提出了一种保持广义决策不变的属性约简方法。文献[11-13]给出了极大相容块的多种快速算法，这样使得极大相容块更容易获得。文献[14]在文献[7]的基础上，利用特征集和极大相容块对不完备数据集进行信息挖掘，分别考虑在有“丢失”值和“不关心”值、只有“丢失”值的两种不完备系统下的特征值和极大相容块生成的二元关系之间的性质。然而利用相似关系拓展的粗糙集模型与经典粗糙集模型具有相同的局限性，即所处理的分类必须是肯定的或者是完全确定的。文献[15]提出了基于变精度粗糙集模型的知识约简方法。文献[16-17]研究了不完备信息系统上的多粒度粗糙集模型。文献[18]研究了不完备信息系统上的三支决策模型。属性约简是粗糙集理论中最重要的研究内容之一，是为了简化原始的信息系统但不影响信息系统的分类能力，从而删除冗余属性的过程[19-21]。本文在文献[14]的基础上，结合变精度的思想，构造了基于极大相容块的变精度粗糙集模型。

2 基础知识

在不完备信息系统中，用U表示对象集，A表示属性集，a∈A。

在不完备信息系统中，对含有缺失值的对象解释是：如果a(x)=*，则有对象x属于每个[(a,v)]中。如果a(x)=?，则有对象x不属于任意[(a,v)]中。因此两种解释的缺失值在不完备信息系统中具有不同的含义。于是将不完备信息系统分成三种：第一种只含有“*”的缺失值的不完备信息系统（如表1）；第二种含有“*”和“?”的缺失值的不完备信息系统；第三种只含有“?”的缺失值的不完备信息系统[6]。

Table 1 Automobile information sheet DS1表1 汽车信息表DS1

定义1在不完备信息系统IS=(U,A,V)中，B⊆A，a,b∈B，Va表示属性a的值域。任取x∈U，定义：

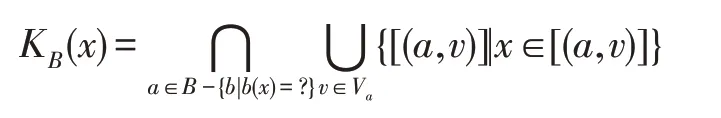
为对象x的特征集。特别地，当B={a}，且a(x)=?，则KB(x)={x}。

文献[14]是在三种不完备信息系统分别描述了特征集的构造，定义1 给出了特征集的一个统一的表达形式。

表1中，A={P,M,S,X}，对象2 的特征集为KA(2)=[(P,low)]⋂([(M,high)]⋃[(M,low)])⋂[(S,full)]⋂[(X,low)]={2,6}，其中当a=M时，有a(2)=*。

定义2[14]在不完备信息系统IS=(U,A,V)中，B⊆A，在对象集U上定义一个二元关系R(B) ：∀x,y∈U，(x,y)∈R(B)当且仅当y∈KB(x)。

当不完备信息系统只含有“*”时，二元关系R(B)满足自反和对称性，与文献[7]中定义的相似关系SIM(B)相同，其中SIM(B)={(x,y)∈U×U|∀a∈B，a(x)=a(y)或者a(x)=* 或者a(y)=*}。当不完备信息系统只含有“?”时，二元关系R(B)满足自反、对称和传递性，即等价关系。当不完备信息系统含有“*”和“?”时，二元关系R(B)只满足自反性，则R(B)称为非对称相似关系。

文献[7]引入了极大相容块的概念，描述了对象相似的最大的集合，即极大相容块中的对象是不可辨识的。

定义3[7]设IS=(U,A,V)是不完备信息系统，B⊆A，Y⊆U，若∀x,y∈Y，都有(x,y)∈R(B)，则称Y是由B确定的相容块。进一步，若不存在相容块X⊆U，使得Y⊂X，则称Y是由B确定的极大相容块。

用C(B)表示由属性集B确定的全体极大相容块的集合，记C(B)={Y1,Y2,…,Yh}，其中Yi⊆U。Cx(B)={Y|Y∈C(B),x∈Y}表示含有对象x的极大相容块的集合。

定义4[14]设IS=(U,A,V)是不完备信息系统，B⊆A，定义一个U上的二元关系S(B)⊆U×U：任意x,y∈Y，(x,y)∈S(B)当且仅当存在Y∈C(B)，使得x,y∈Y。

显然有二元关系S(B)满足自反性和对称性，且S(B)⊆R(B)。

性质1[14]在不完备信息系统IS=(U,A,V)中，B⊆A，x∈U，则对于∀Y∈Cx(B)，有Y⊆KB(x)。

3 基于极大相容块的广义变精度粗糙集模型及其属性约简

3.1 广义变精度粗糙集模型

本节将不完备信息系统中基于极大相容块的粗糙集模型[7]推广为变精度粗糙集模型。

首先给出子系统中的极大相容块与原系统中的极大相容块之间的关系。

性质2在不完备信息系统IS=(U,A,V)中，B⊆A，∀X∈C(A)，存在Y∈C(B)，使得X⊆Y。且C(B)中的极大相容块Y都是由C(A)中的一些极大相容块X的并构成的，即：

证明首先证明X⊆Y，若X∈C(A)，由定义3，∀x,y∈X，则有(x,y)∈R(A)，因为R(A)⊆R(B)，所以(x,y)∈R(B)，X是由属性集B确定的相容块，但不一定是极大的。肯定存在极大相容块Y∈C(B)，使得X⊆Y。

接下来证明Y={X|X∈Cx(A)}。易知Y⊆{X|X∈Cx(A)}，下证{∈Cx(A)} ⊆Y。对于∀y∈{X|X∈Cx(A)}，则 有x,y∈X,B⊆A，(x,y)∈R(A)，有(x,y)∈R(B)，又因为X⊆Y，所以{X|X∈Cx(A)}⊆Y。□

定义5在不完备信息系统IS=(U,A,V)中，对于任意B⊆A，任取X⊆U，β∈(0.5,1]，称

为X关于B基于C(B)的β-下近似，称

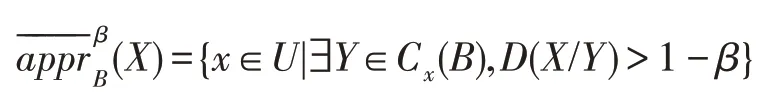
为X关于B基于C(B)的β-上近似。其中D是P(U)上的包含度，|Y|表示Y中元素的个数，即：

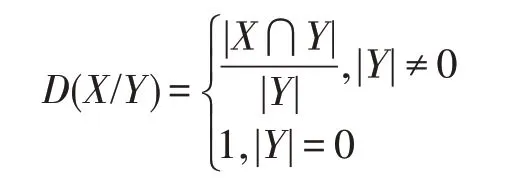
称此模型为基于极大相容块的悲观变精度粗糙集模型。

定义6在不完备信息系统IS=(U,A,V)中，对于任意B⊆A，任取X⊆U，β∈(0.5,1]，称

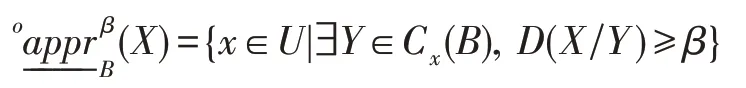
为X关于B基于C(B)的β-下近似，称

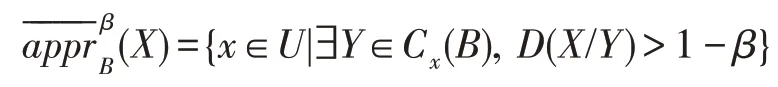
为X关于B基于C(B)的β-上近似。

称此模型为基于极大相容块的乐观变精度粗糙集模型。

定义7在不完备信息系统IS=(U,A,V)中，对于任意B⊆A，任取X⊆U，β∈(0.5,1]，令、分别表示X关于B的悲观精度和乐观精度，即：

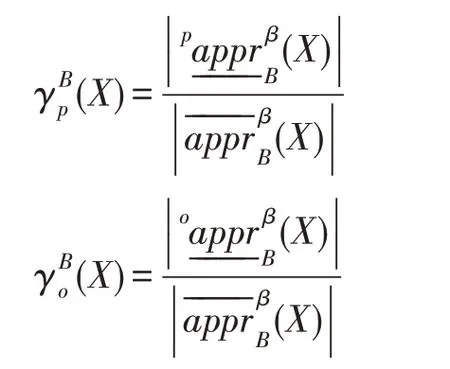
性质3

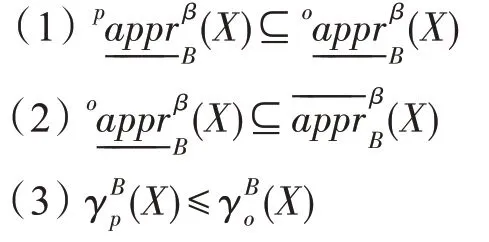
证明（1）∀x∈，则∀Y∈Cx(B)，满足D(X/Y)≥β，故x∈。

（2）因为β∈(0.5,1]，β＞1-β由（1）可知，D(X/Y)≥1-β，故。

（3）由（1）可证。 □

由性质3（3）可知，与基于极大相容块的悲观变精度粗糙集模型相比，乐观变精度粗糙集模型的精度更高。

定义8在不完备信息系统IS=(U,A,V)中，B⊆A，任取X⊆U，则和分别称为X关于B的β-上下近似，β∈(0.5,1]，即：

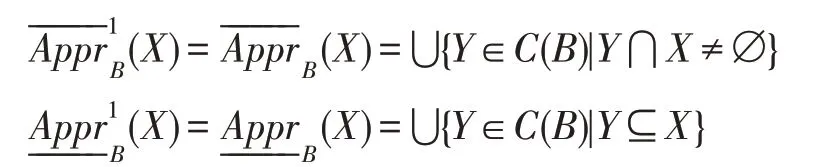
定理1在不完备信息系统IS=(U,A,V)中，B⊆A，任取X⊆U，则有：

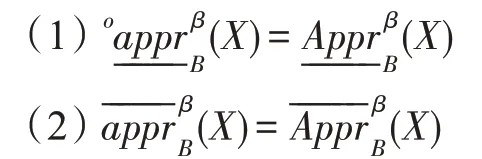
证明（1）显然有，接下来要证，∀y∈，y属于某一个极大相容块Y∈C(B)，即Y∈Cy(B)，并且D(X/Y)≥β，则y∈。

同理可以证得（2）成立。 □

定理1 表明在不完备信息系统中利用极大相容块定义的两种上下近似算子是相同的。下近似算子统一用表示，上近似算子用表示。

称DS=(U,A,V,D,G)为不完备决策信息系统，其中(U,A,V)是不完备信息系统，D是决策集，G是决策值域。

定理2设DS=(U,A,V,D,G)是不完备决策信息系统，B⊆A，0.5 ＜α,β≤1，RD是U上由D导出的等价关系，U/RD={D1,D2,…,Dr}，容易验证和满足以下性质：

（1）若X1⊆X2，则：

预警发布后加强大坝、溢洪道、输水洞、排水沟、滤水坝址等部位的巡视检查，库水位每上升2 m巡查一次，同时监测测压管水位，发现问题及时报告处理。当水位达到89.5 m即溢洪道底坎高程时，加强对溢洪道和闸门的检查，同时注意及时打捞闸门附近的大型漂浮物。

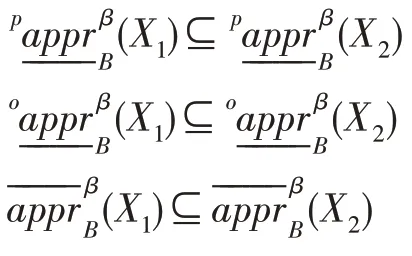
（2）若α≤β，则：

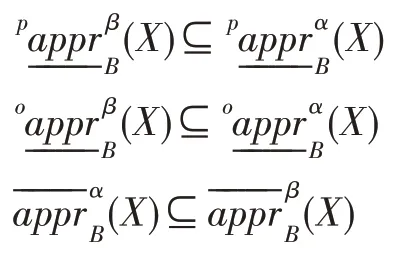
3.2 广义变精度粗糙集模型上的属性约简

基于上一节中提到的广义变精度粗糙集模型，本节定义几种属性约简的概念和该模型上的β-上(下)分布约简方法。

定义9设DS=(U,A,V,D,G)是不完备决策信息系统，对于B⊆A，若C(B)=C(A)，则称B是分块协调集。进一步，若∀B′⊂B，C(B′)≠C(A)，那么B是分块约简。

定义10设DS=(U,A,V,D,G)是不完备决策信息系统，B⊆A，U/RD={D1,D2,…,Dr}。对于β∈(0.5,1]，记：

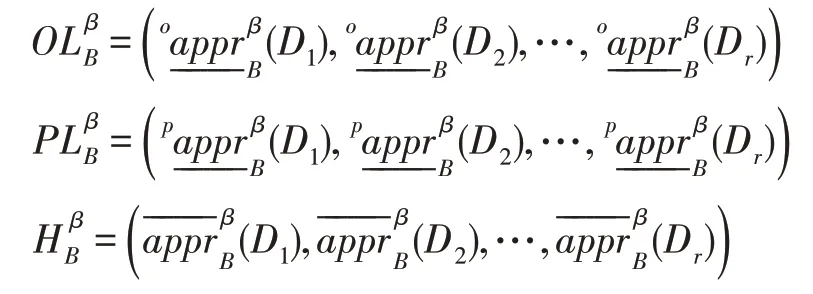
定理3设DS=(U,A,V,D,G)是不完备决策信息系统，分块协调集必是β-上（下）分布协调集。

证明由属性集A确定的极大相容块的集合为C(A)={X1,X2,…,Xm}，若B⊆A，B为该系统的一个分块约简，则有C(B)=C(A)，由定义6 可知，=，∀Dj∈U/RD，分块协调集必是乐观β-下分布协调集，同理可证分块协调集是悲观β-下分布协调集和β-上分布协调集。 □

定义11设DS=(U,A,V,D,G)是不完备决策信息系统，β∈(0.5,1],U/RD={D1,D2,…,Dr},C(A)={X1,X2,…,Xm}，记：

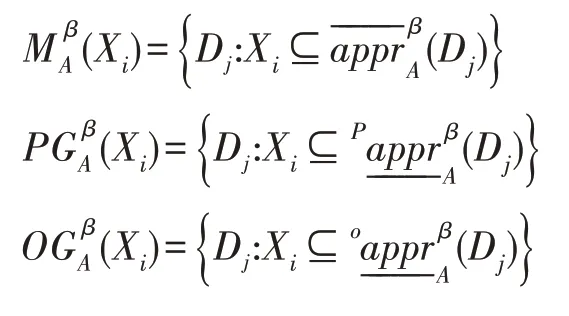
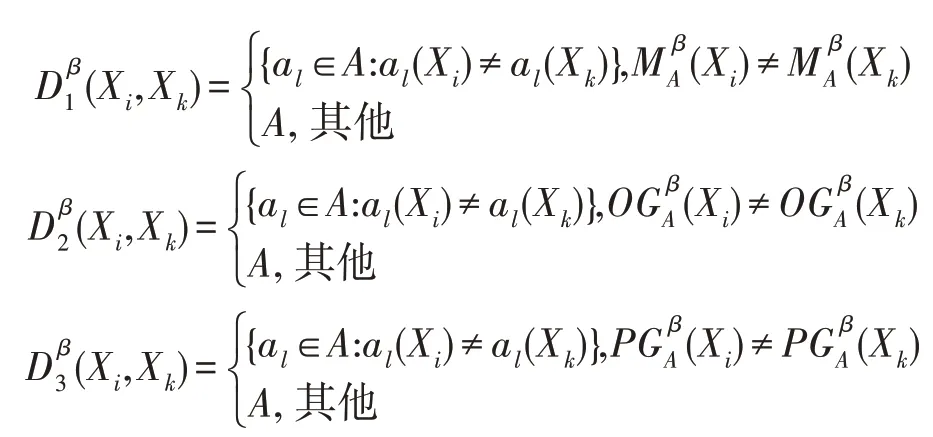
注1当信息系统中a(x)=?时，该对象x所在极大相容块与其他极大相容块的辨识属性集一定包含属性a。

定理4设DS=(U,A,V,D,G)是不完备决策信息系统，令C(A)={X1,X2,…,Xm}，β-上（下）分布可辨识属性集具有以下性质，其中i,k,s≤m：

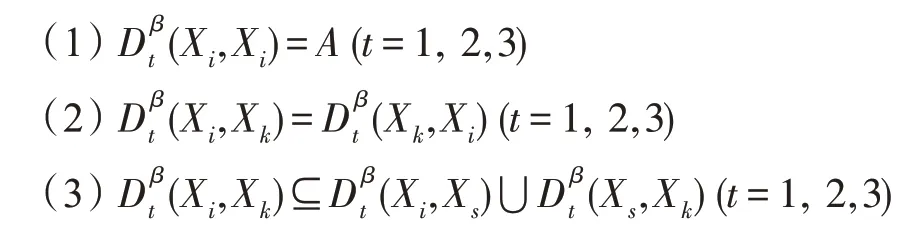
证明与文献[15]中定理3.3的证明过程类似。□

定理5设DS=(U,A,V,D,G)是不完备决策信息系统，B⊆A。

证明一方面，当时，{Dj:Xi⊆，设B是β-上分布协调集，由定义10 可知，即∀Dj∈U/RD=，因此有。由性质2 可知，Xi、Xk肯定也是由属性集B确定的相容块，但不一定是由属性集B确定的极大相容块。存在极大相容块Yi,Yk∈C(B)，Xi⊆Yi，Xk⊆Yk，则有，因此存在a∈B，使得a(Yi)≠a(Yk)，那么a(Xi)≠a(Xk)，即证得该式子B⋂(Xi,Xk)≠∅成立。另一方面，∀Xi,Xk∈C(A)，当时，假设B⋂(Xi,Xk)=∅，则∀a∈B，a(Xi)=a(Xk)，由性质2 知，Yi,Yk∈C(B)，Xi⊆Yi，Xk⊆Yk，a(Yi)=a(Yk)，一定存在al∈A，且al∉B，使得al(Xi)≠al(Xk)。故存在Dj∈U/RD，有，则B不是β-上分布协调集。

同理可以证得（2）和（3）成立。 □

在不完备决策信息系统DS=(U,A,V,D,G) 中，(Xi,Xk),i,k≤m)表示为不完备DS的β-上（下）分布可辨识矩阵，A={a1,a2,…,as}，记：

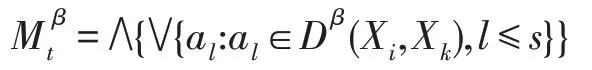
其中，i,k≤m，t=1,2,3，Mβ t称为β-上（下）分布可辨识公式。

4 实例分析

对于只含有“?”的缺失值的不完备决策信息系统[7]，R(A)满足自反、对称和传递性。S(A)⊆R(A),故极大相容块构成的集合C(A)不仅是U上的一个覆盖还是一个划分，因此在这类决策信息系统中与完备决策信息系统中利用第3 章中的方法求取属性约简的过程相同。

下面在另外两种不同的不完备决策信息系统中验证上一章给出的属性约简方法。

例1表1 是只含有“*”的不完备信息表DS1，条件属性集为A={P,M,S,X}，决策属性集为D={D1=good,D2=poor,D3=excellent}，计算0.7-上分布约简和0.7-下分布约简。

记μB(Y)=(D(D1/Y),D(D2/Y),…,D(Dr/Y))为极大相容块Y关于属性集B在不完备信息系统中的广义决策分布函数。

由决策属性D在U上产生划分为：

由定义1 可得对象的特征集：

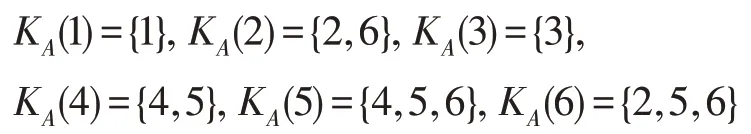
由条件属性集A确定的极大相容块的集合为：

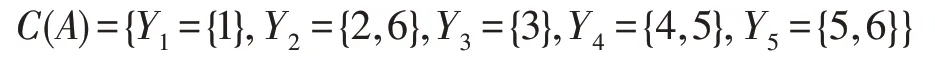
由定义2 可得对象的特征集生成的二元关系：

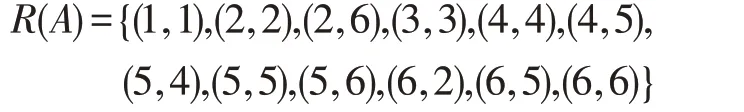
由定义4 可得极大相容块生成的二元关系：

得到极大相容块的广义决策分布为：

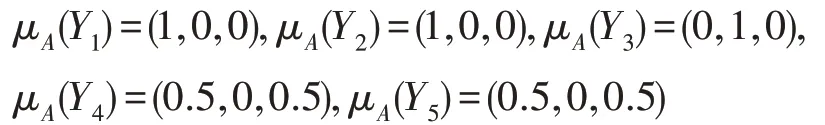
决策等价类U/RD的0.7-上近似：

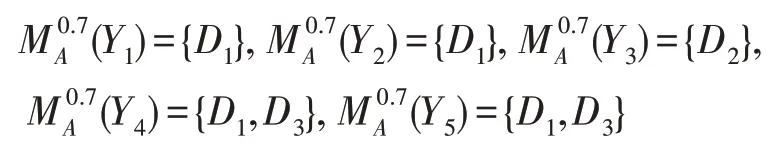
从而得到极大相容块之间的可辨识矩阵（表2），则不完备决策信息系统的0.7-上分布辨识公式：

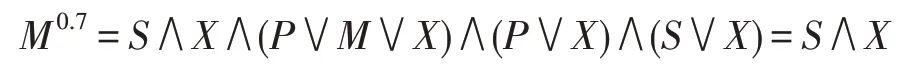
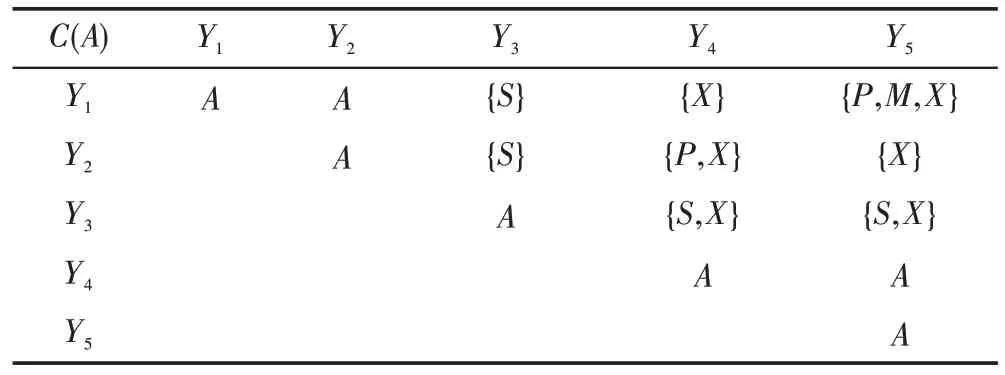
Table 2 Discernible attribute matrix of DS1表2 DS1 的可辨识属性矩阵

由此可知{S,X}是此不完备决策信息系统的0.7-上分布约简。同样计算乐观的0.7-下分布约简的结果也是{S,X}。

属性约简的结果与文献[5]和文献[22]相同，与文献[22]中基于对象间的可辨识矩阵比较，本文提出的基于极大相容块的方法压缩了可辨识矩阵规模，进一步简化了运算过程，节省了存储空间。

而DS1的悲观0.7-下分布约简的结果是{S,X,P}和{S,X,M}。

例2含有“ *”和“ ?”的不完备的决策信息表DS2（表3），决策属性的值域为d={d1,d2,d3}，对象集为U={x1,x2,x3,x4,x5,x6,x7,x8}，条件属性集为A={a1,a2,a3,a4}，决策属性d，计算0.7-上分布约简。

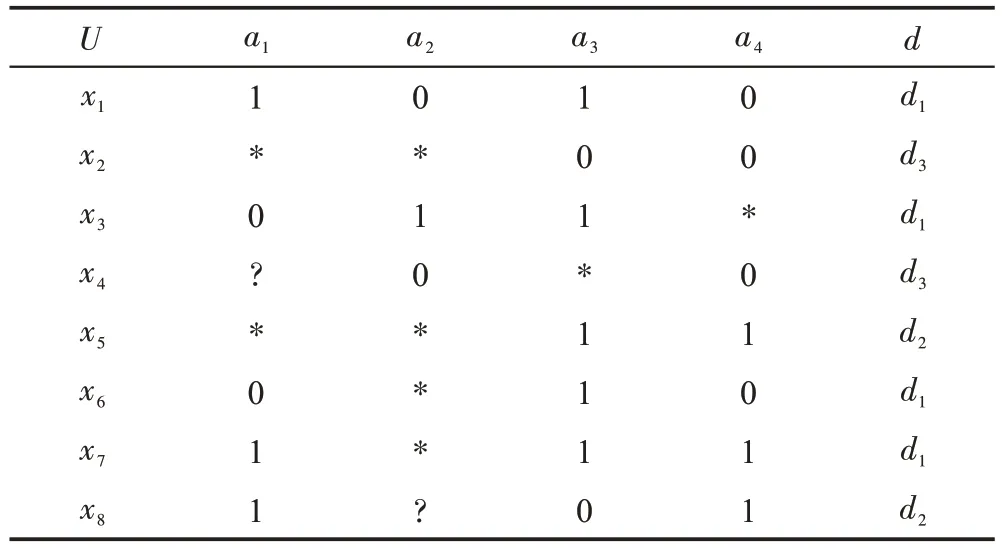
Table 3 Incomplete information DS2表3 不完备信息表DS2

其中由d产生的划分为：

由条件属性集A确定的极大相容块的集合为：

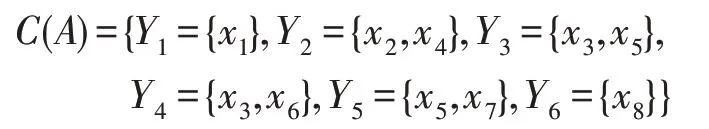
极大相容块的广义决策分布为：

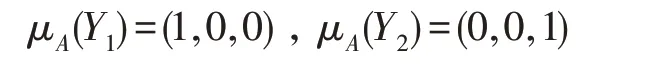
则有

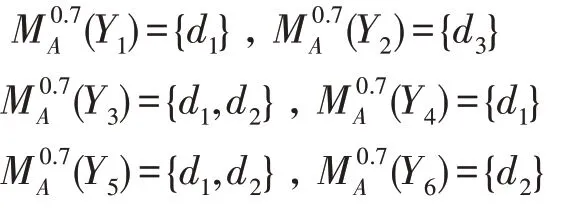
从而得到各个极大相容块之间的辨识属性集（表4），不完备决策信息系统的0.7-上分布辨识公式：

Table 4 Discernible attribute matrix of DS2表4 DS2 的可辨识属性矩阵

因此{a3,a4}和{a1,a2,a4}是此不完备决策信息系统DS2的0.7-上分布约简。这个结果与DS2的乐观和悲观的0.7-下分布约简相一致。

这个结果与DS2的乐观和悲观的0.7-下分布约简相一致。

基于3.1 节提出的广义变精度粗糙集模型，给出一种计算不完备信息系统的β-上分布约简的算法。

为了进一步验证该算法的有效性。本文在UCI数据集中选择了5 组含缺失值的数据，数据基本信息如表5 所示。根据上述算法，其中令β=0.7，得到0.7-上分布约简结果（表6）。

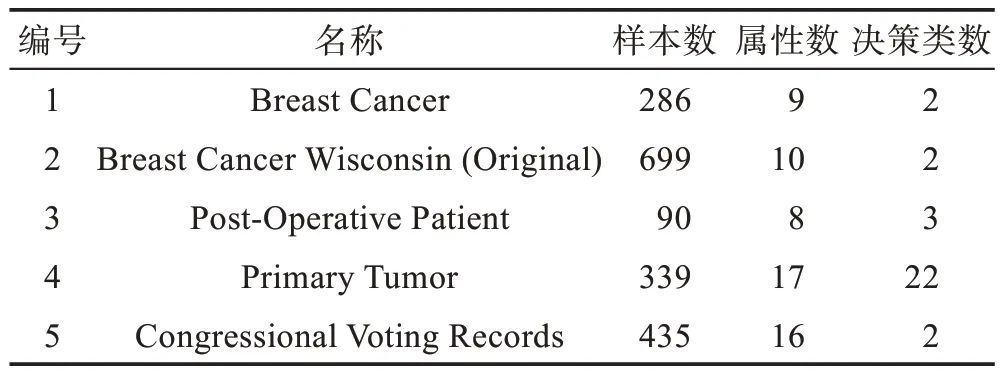
Table 5 Description of data sets表5 数据集的基本信息

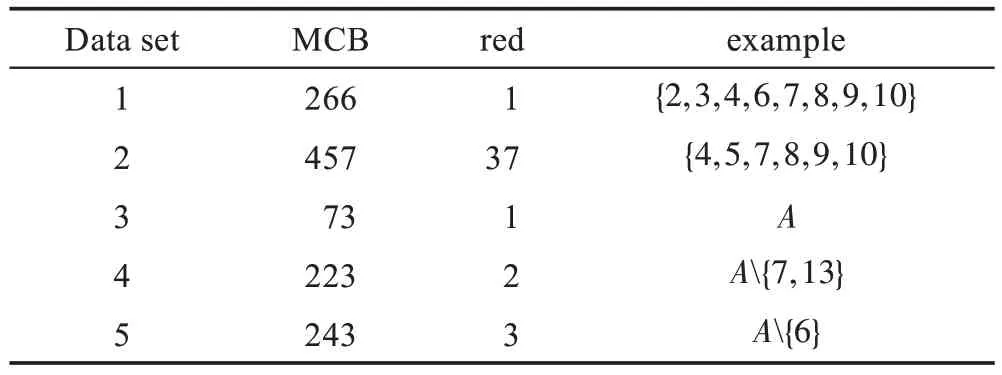
Table 6 Result of reduction表6 约简的结果

注2在约简结果中，数字k代表第k-1 个条件属性。A表示该数据集的条件属性的集合，MCB 表示极大相容块。

5 结束语

本文将变精度粗糙集模型和极大相容块相结合，在不完备信息系统中建立了基于极大相容块的广义变精度粗糙集模型，构造了极大相容块间的可辨识属性集，进而利用布尔计算方法获取属性约简。为区分两种缺失值，对含有“?”的极大相容块与其他极大相容块间的可辨识属性集做了特定的要求。此约简方法可有效地缩小可辨识矩阵的规模，进一步简化了计算属性约简的过程，在一定程度上能够有效地节省计算时间和存储空间。