学为中心,问题导向
2020-05-12金一民
金一民

摘要:学习要在学中问,于问中学。基于这样的理解,构建“学为中心,问题导向”的小学数学“学问”教学模式。该教学模式分为四个环节——“先学”:带着问题进课堂;“合学”:聚合智慧;“讲学”:暴露思维;“后学”:带着问题出课堂。各个环节中,学生围绕问题展开学习,教师充分发挥对学习的诊断和指导作用。
关键词:学中问问中学教学模式小学数学
“学习”是一个经典而又时尚的话题,人们对于“学习”的研究伴随和促进着人类文明的发展。什么是学习?不同的人群、不同的角度有不同的解释。如果要在严格的定义之外,给“学习”寻找一个通俗易懂的解释,我们认为,就是中国古人所说的“做学问”。这样的遣词蕴含着丰富的智慧,揭示了问题的本质:学习要在学中问,于问中学(或者说,以学求问,以问导学)。李政道先生说过:“要创新,需学问。只学答,非学问。问愈透,创更新。”“学”和“问”也正是回答“钱学森之问”的核心所在。
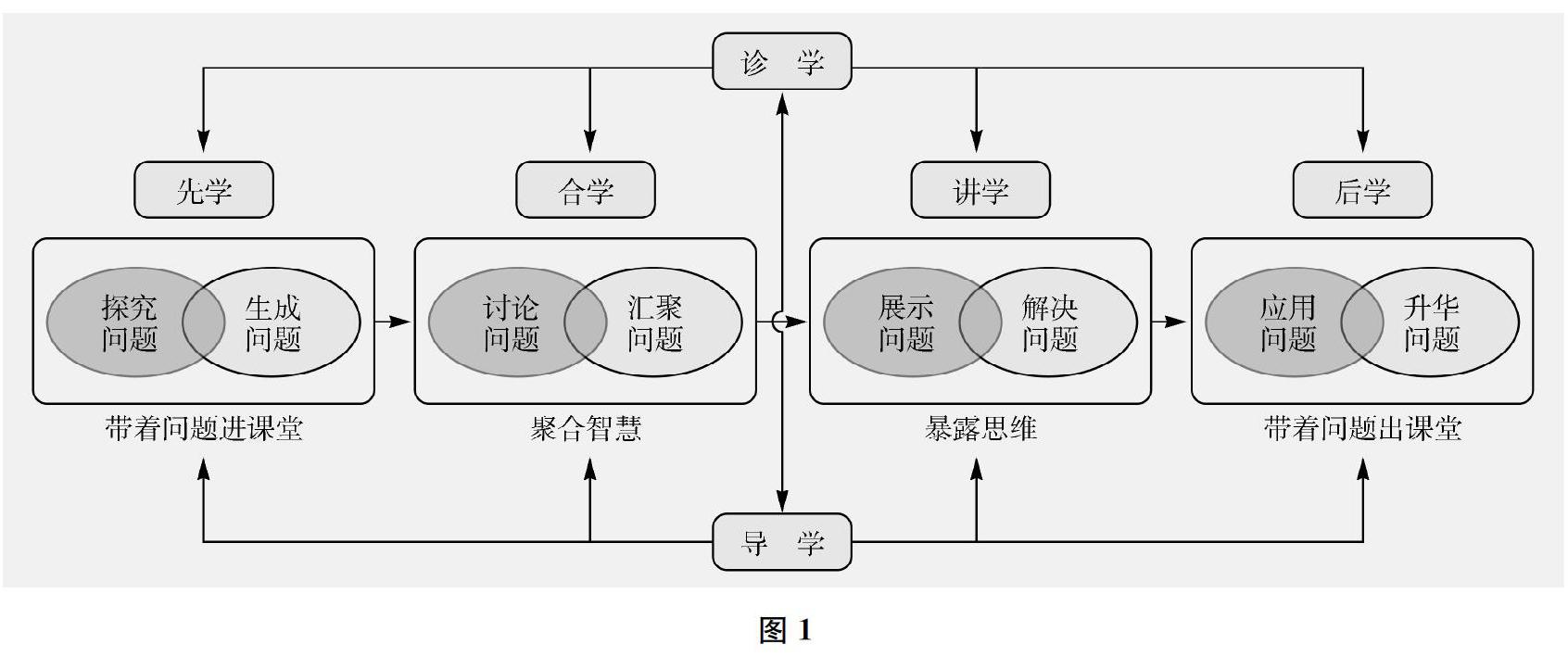
基于这样的理解,我校构建了“学为中心,问题导向”的小学数学“学问”教学模式(其结构图见下页图1)。该教学模式分为先学、合学、讲学、后学四个环节。各个环节中,学生围绕问题展开学习,教师充分发挥对学习的诊断和指导作用。具体介绍如下:
一、“先学”:带着问题进课堂
“先学”就是前置于课堂的学习。传统的课堂学习往往始于上课铃声。对于一些探究容量较大的内容,有限的课堂时间无法保证学生深度的学习参与。通过“先学”,可以引导学生利用课前充分的时间(和空间)积极探究,激活“前经验”,获得“前理解”,形成“前概念”,带着问题进入课堂学习,让学习更具有针对性。
(一)“先学”之“教”:分析和设计问题
倡导学生“先学”并不是弱化教师的作用,相反,对教师的设计和指导提出了更高的要求。教师通过学情诊断,分析、设计一些“大问题”,从而实施学习指导。“大问题”就是基于核心知识的、具有较大探索空间和思维容量的问题。学生对“大问题”的探究能够促进其对知识的理解,生成有助于深度学习的问题。
例如,苏教版小学数学六年级下册《认识圆柱》一课,传统的教学往往是让学生带着一些圆柱形的物体进入课堂,通过观察、测量等方式认识圆柱的特征。这样的教学,学生的思维停留在低阶的识记层次。本课中,认识“圆柱上下两个圆的周长就是侧面展开长方形的长”是教学的难点,又是后续圆柱表面积和体积计算的关键,应该让学生充分体验、深刻理解。为此,我们设计了几个“大问题”,编制出一份“先学单”(见图2),引导学生先行探究。
(二)“先学”之“学”:探究和生成问题
区别于一般的预习,“先学”之“学”是基于“大问题”的深度探究,需要观察、操作、抽象、推理、分析、综合、反思、创造等多种活动的参与,需要人际交往、人機互动等多种方式的融合。“先学”中,学生的发现和未能解决的问题都是后续学习重要的资源。
仍以《认识圆柱》一课为例,“做圆柱”是一项实践性、探究性很强的学习活动。要能做出一个圆柱,首先要基于对身边圆柱形物体的观察、测量,包括通过拆解的方式进行研究;其次要不断尝试、摸索、调整、修正,甚至重来。在这个“做数学”的过程中,学生得到了一些重要的发现。如一位学生总结圆柱的特征有:两边的口子上都是完全相同的圆;有无数条高,沿着一条高剪开,展开后是一个长方形;有3个面。学生也遇到了不少实际的困难,如不能封口、不知道(底)圆到底有多大。
这些来自学生实践探究的发现和问题反映了学生真实的思考。当然,其中还掺杂着一些非本质的特征,需要进一步的学习。学生带着自己的发现和疑惑进入课堂,不仅能聚焦学习的重点和难点,有利于知识的理解和掌握,而且能激发学习的需要,促进情感、态度和价值观的发展。
二、“合学”:聚合智慧
学习不仅仅是一种自我建构,还是一种人际交往。学习科学研究表明,不论从知识层面还是情感层面,交往都能有效促进学生的学习和发展。“合学”就是合作学习,主要方式是小组学习。当学生经过“先学”“自学”后,“合学”就成为学生学习的需要。
(一)“合学”之“学”:讨论和汇聚问题
“合学”之“学”主要有两大任务。第一是分享和交流。基于“先学”的成果,小组成员在小组中分享自己的观点,与其他成员进行交流,吸收他人的智慧,完善自己的成果。在这一过程中,每个人的观点都能得到表达和反馈,每个人的学习都在真正发生。第二是碰撞与整合。有效的学习应该是在吸收他人智慧基础上的提升。通过碰撞和整合,形成小组的观点和未能解决的问题。这些观点和问题相比于个人的,更具深刻性、综合性。
仍以《认识圆柱》一课为例,经过“合学”,不同的小组形成了不同的成果。有的小组解决了“做多大的圆形‘盖,才能和侧面完美拼接”的问题,如:用“两个端点都在圆上的线段中直径最长”来解决,用“圆的周长就是侧面长方形的长”来解决等。当然,也有小组未能解决这一问题,但在小组合作的过程中,他们经历了尝试、修正、完善等过程,那同样是有效的学习。
(二)“合学”之“教”:观察和筛选问题
“合学”中,教师的“诊学”主要体现在对学生“先学”情况的诊断。教师可以通过批阅学生的“先学单”或访谈、测试等方式,了解学情。同时,教师要注意收集和筛选学生小组学习中生成的观点和问题,作为后续学习的资源。
仍以《认识圆柱》一课为例,教师在巡视中发现,学生都能发现“圆柱有一个侧面和两个底面”“侧面展开是一个长方形”“底面是相同的两个圆”等结论,而在“底面圆到底要画多大”这个问题上争论不休。于是,教师把这一问题筛选出来,作为后续全班讨论的关键问题。
“合学”中,教师的“导学”主要体现在对学生“合学”过程的指导。通过对“合学”规则的引导,培养学生的合作意识和品质。比如,可以确定以下小组讨论规则:(1)组长负责讨论的组织工作,确定发言顺序,做好讨论记录;(2)组员汇报时要重点突出、条理清晰、简明扼要;(3)其他组员要认真倾听、思考,捕捉汇报中的关键点,在小组讨论时提出来,引发交流碰撞;(4)组员讨论时要基于前面的意见提出自己的观点,而不能重复前面的观点;(5)讨论结束后要总结小组学习的成果,提出最重要的发现或未解决的问题,提交全班交流;(6)开展小组评价,确保每一位组员的意见在组内都得到尊重,得到学习支持。事实上,核心素养所倡导的尊重、信任、包容、交往等必备品格并不只是通过德育来培养的,日常的学习活动才是其培养的主要途径。
三、“讲学”:暴露思维
传统教学强调“听讲”,即教师讲,学生听。这里说的“讲学”,是学生讲,师生听。美国贝瑟尔国家实验室研究提出的“学习金字塔”理论表明,学习效果最好的方式是“讲给别人听”。通过“讲学”,学生能暴露自己的思维过程,也能进一步组织自己的思维成果,有利于进一步的学习。
(一)“讲学”之“学”:展示和解决问题
“讲学”之“学”就是由小组代表进行全班展示交流。“讲学”的过程,对表达者来说是一个“再组织”的过程。要把学到的东西讲出来,必然基于对所学内容的深刻理解,有利于“知识和技能”目标的达成。“讲学”以语言为载体(语言是思维的工具),有利于思维的发展。“讲学”实际上是一种“元认知”,有利于“过程与方法”目标的实现。“讲学”又是人际交往的过程,有利于“情感态度和价值观”的发展。“讲学”的过程,对倾听者来说是一个反思提升的过程。讲学的内容来自学生共同研究的成果,是学生真实思维的展现,容易引起倾听者的关注。
例如,苏教版小学数学四年级上册《认识平行》一课,在“讲学”过程中,各小组展示出不同的画平行线的方法。比如在方格纸上画、利用直尺的两边画、利用平行线之间距离处处相等的知识画等。学生把每一种方法的相关背景和思考过程表达出来,成为学习的最佳资源。
(二)“讲学”之“教”:串联和提升问题
“讲学”中,教师退居到“听”的位置:通过“听”小组的展示,诊断观点或问题背后的思考和价值;然后,通过“串联”学生的回答,引发课堂的“交响”,让学习深度发生。教师可以通过“你是怎么想的呢?”“为什么这样想呢?”等问题启动学生的元认知,通过“谁有不同意见?”“谁有补充?”等问题发展学生的批判性思维。
仍以《认识平行》一课为例,有小组在展示画平行线的方法时,提出了“用三角板直角边靠住直尺边移动”的方法。这种方法对学生来说比较难,也很少有学生想到,而这种方法里隐含着丰富的思维价值。通过小组展示、全班互动、教师串联,我们充分地发掘了这样的价值——
生我们可以用一把直尺和一个三角板。将三角板的一条直角边靠住直尺的一条边,然后移动三角板,可以画出不同距离的平行线来。
師对于刚才这位同学的方法,谁有疑问?
生为什么这样画出的一定是一组平行线呢?
生因为三角板靠住直尺的一条边移动,这样的方式就是“平移”,我们就能得到一组平行线。
……
师还有什么想问的吗?
生你是怎么想到这种方法的呢?
生我们是从窗户的平移想到的。这把直尺相当于窗户的轨道,沿着轨道平移,我们就想到了这种方法。
……
四、“后学”:带着问题出课堂
“后学”就是后置于课堂的学习。传统的课堂学习往往止于下课铃声。事实上,课堂的结束并不代表学习的结束,而是新的学习的开始。相比于课堂学习,“后学”的时间更长、空间更大。学生带着问题出课堂,可以应用所学开展更加深入、广泛的探究。
(一)“后学”之“教”:启发和拓展问题
“后学”之“教”体现在教师对学生后续学习的“诊”和“导”上。一方面,教师要捕捉课堂中的信息,将一些课堂上无法解决的问题作为后续探究的主题。另一方面,要通过“我是怎样学的?”等问题,以及“课堂一得”“数学日记”等形式,引导学生进行课后反思和总结,从“学会”转向“会学”,并将所学应用到现实生活中。
例如,苏教版小学数学四年级下册《用数对确定位置》一课的课尾,教师提出拓展性问题:数对是谁发明的呢?数对在生活中有什么应用呢?你还想学习哪些有关数对的知识?这些问题进一步激发了学生学习数学的好奇心和想象力,让他们投入到富有创造性的学习中——数对来自生活中的数学表达(笛卡儿从蜘蛛结网中得到启发),我们经常见到的统计图、经常使用的导航系统都是数对知识的应用;我们今天学习的是用数对确定平面图形上的位置,那么在直线(一维)上和空间(三维)中如何确定位置呢?
(二)“后学”之“学”:应用和升华问题
“后学”之“学”与课堂学习相比,更多体现在课堂知识的应用和升华上。学习内容与现实生活更为贴合,具有一定的主题性、综合性,学生面临的往往是复杂、真实的情境:条件不确定、问题不明确、结果不唯一……需要经历更多元的学习和思维过程。学习方式上,以实践、体验、探究为主,要经历发现和提出问题、分析和解决问题的过程。
例如,苏教版小学数学五年级下册《折线统计图》一课的课后,学生开展了以常熟市社会经济生活发展为主题的研究。他们自由组成学习小组,选择研究主题。有的小组围绕家庭收入、汽车数量、住房变化等展开研究,反映社会经济的发展;有的小组研究城市空气质量、交通拥堵、水质污染等状况,反映片面追求经济发展带来的社会问题。他们实地考察、走访调查、搜集资料,利用数学方法统计分析,撰写报告,提出建议,制作PPT展示成果。这样的学习弥补了课堂学习的不足,体现了学生作为公民的社会责任感和良好品格,培养了学生的创新精神和实践能力,有利于学生核心素养的发展。
