基于行星际闪烁望远镜的数字波束合成技术研究*

杨 轩，陈林杰，荣 健，颜毅华,3

(1. 电子科技大学，四川 成都 610066； 2. 中国科学院国家天文台，北京 100101；3. 中国科学院大学，北京 100049)

国家重大科研装备研制项目子午工程二期列入了国家发改委十大优先支持项目，该工程连续监测地球表面20～30 km以上到几百千米的高层大气、电离层和磁层以及十几倍地球半径以外的行星际空间环境中的电磁场、电场、中高层大气的风场、密度和成分、电离层、磁层和行星际空间的有关参数。

行星际闪烁是指来自于遥远致密射电源的电磁波在穿过太阳系行星际空间时，被太阳风等离子散射形成的射电波强度和相位的一种随机起伏现象。通过研究这种闪烁现象，可以研究致密源的角结构，并测量太阳风速度和太阳风等离子不规则结构，观测数据对理论研究和实际应用有重要作用[1]。行星际闪烁的地基测量是监测行星际空间的一种经济、有效的遥感技术。以天然射电源或卫星下行通讯链为射电信标，以地基望远镜的单站或多站组网方式接收射电信号，行星际空间作为射电传播路径的介质能影响射电的传播特性。通过对透射的射电信号强度、传播时延、相位变化等参量的测量，必要时加以反演计算，可以遥测行星际空间的结构及其时空变化特征。

目前，国外多个国家已经利用现有望远镜开展了对行星际闪烁的研究，国内由中国科学院空间中心牵头建设的子午二期行星际闪烁观测设备目前正在进行技术储备，通过三站联合观测，并分析数据，有望在背景太阳风速的三维大尺度分布和太阳活动周演化、行星际日冕物质抛射的三维空间层析反演和时变追踪、太阳风的动力学湍流幅度等方面取得重要科学进展[2]。

对于行星际闪烁望远镜，其中的一项关键技术是数字多波束合成技术。数字多波束合成亦称空域滤波器，是阵列处理的一项主要技术。目前，它在射电天文、雷达、声呐、导航、无线电通信和地震监测等多方面得到了广泛应用。本文主要讨论数字多波束合成在射电望远镜上的应用。数字多波束合成实质是充分利用天线阵列在不同位置的阵元所获得的空间信号信息，通过对各阵元进行加权，达到增强期望信号、抑制干扰的目的。其优点有：可形成单个或多个独立可控的波束而不损失信噪比；波束特性由权矢量控制，灵活多变；天线具有较好的自校正和低旁瓣能力；方便后续进行阵列信号处理，以获得优良性能[2]。利用这一技术可形成多个主波束，实现对天空多个射电源的同时观测。

1 行星际闪烁望远镜

在子午二期行星际闪烁望远镜的设计中，分析比较日本名古屋(Nagoya)四站和印度乌蒂(Ooty)单站的行星际闪烁设计方案和观测经验，提出了一主站两辅站的设计方案。主站位于内蒙古正镶白旗明安图镇，采用大型可转动的抛物柱面天线；两辅站分别位于阿巴嘎和克什克腾，采用全可动的抛物面天线。三站的地理坐标近似构成等边三角形，任两站之间的基线长度近似200 km，如图1。行星际闪烁探测设备主要是测量射电源强度闪烁的时间序列，采用单站观测的功率谱拟合和三站联测的互相关时延，快速获得不同空间区域处太阳风的速度、电子密度扰动的非约化功率谱等物理参数，追踪太阳风和日冕物质抛射扰动在行星际空间的加速、传播和演变。

子午二期行星际闪烁望远镜的主站由3个抛物柱面天线并排放置，每个柱面天线在南北方向140 m，在东西方向40 m，如图2。为了快速扫描天空并寻找其他科学目标，柱面天线设计成可以在东西方向转动，但不跟踪天空中的源。通过转动，在不同的时间指向不同的天区，可以完成整个天区的快速扫描覆盖。另外，在主站还有一个20 m的抛物面天线，也可以用于行星际闪烁的观测。两个辅站各有一个约20 m的抛物面天线。在每个站点，天线不仅可以双频率、单站点、独立地观测射电源，而且也可以双频率、多站点联合工作。通过这种方式，一方面可以利用主站的天线获得很高的灵敏度，观测到天空中更多的射电源，另一方面可以利用对强射电源进行多站相关，获得更为精确的太阳风速度等信息，从而更好地重建三维太阳风结构。

图1 行星际闪烁望远镜的布局

Fig.1 Configuration of the IPS Telescope

图2 行星际闪烁望远镜主站阵列

Fig.2 Main site array of IPS Telescope

每个柱面天线有一个聚焦线，沿着聚焦线放置304个馈源接收射电信号，可以在327 MHz和654 MHz下同时或者单独工作。每个馈源连接一个低噪声放大器，信号经放大、带通滤波后经过一个模数转换器进行数字化。数字信号通过光纤传输到室内接收机，然后进行数字多波束合成，最后输出不同方向多个射电源的观测信号。本文主要对行星际闪烁望远镜主站柱面天线的数字多波束合成技术进行研究[3]。行星际闪烁望远镜的主要参数和技术指标如表1。

表1 行星际闪烁望远镜的主要参数和技术指标

*仅辅站抛物面天线在此频率观测。

2 阵列信号的建模

假设空间有一个射电源，且有N个阵元组成的均匀线阵阵列接收信号。将第1个阵元位于坐标原点，作为参考阵元。在信号是窄带的情况下，若参考阵元接收的信号用S(t)=s(t)ejwt表示，则第i个阵元接收的信号可以表示为Si(t)=s(t-ti)ejwte-jwti。均匀线阵接收信号模型如图3。

图3 均匀线阵接收信号模型

Fig.3 Received signal model of uniform linear array

设a(θ)为导向矢量，则a(θ)=[1,e-jwt1, ...,e-jwti, ...,e-jwtN-2,e-jwtN-1]T，其中第i个阵元相对于参考阵元的延时ti=idsinθ/c。干扰和期望信号为同频率的窄带信号，但入射角度不同，且与期望信号不相关。噪声信号为平稳的、零均值、方差为σ2的高斯白噪声，各阵元接收的噪声间互不相关，且与期望信号不相关。

3 阵列方向图定义

阵列天线的方向图是按一定方式排列的天线阵列的权矢量对来自空间不同方向的信号的阵列响应。阵列的方向函数F(θ)可以表示为

F(θ)=WHa(θ)，

(1)

其中，W为波束合成算法得出的权矢量。方向函数表征波束合成后，天线对各个方向的信号的增益。对(1)式取绝对值并归一化，然后取对数，阵列的方向图P(θ)可以表示为

(2)

由(1)式和(2)式可以得出，当阵列的权矢量改变时，对来自不同方向的空间信号来说，会有不同的响应，从而改变阵列方向图P(θ)的指向。

4 数字波束合成算法

数字波束合成算法是通过对阵列不同位置的阵元进行加权，使阵列方向图的主瓣对准期望信号入射方向，低旁瓣对准干扰方向，以此达到增强期望信号、抑制干扰的目的，包括常规数字波束合成算法以及自适应数字波束合成算法。

4.1 常规数字波束合成算法

常规数字波束合成算法的权值是固定的，与输入信号无关。权值等于期望信号的导向矢量。因此，在期望信号方向的响应为F(θ0)=a(θ0)Ha(θ0)=N；其中，θ0为期望信号入射角，N为阵元个数。这时，各通道的信号同相相加，阵列在期望信号θ0方向的信号增益最大。

4.2 自适应数字波束合成算法

自适应数字波束合成算法是根据信号的先验知识和一定准则，调节阵列的权矢量，使天线阵列方向图在期望方向形成主波束，在干扰方向形成零陷，从而对干扰形成抑制。自适应波束合成权值与输入信号有关，且随着电磁环境的变化自适应地调整，能够实现对期望信号的跟踪[4-5]。自适应波束合成系统框图如图4。

图4 自适应波束合成系统框图

Fig.4 Block diagram of adaptive beamforming system

线性约束最小方差(Linearly Constrained Minimum Variance, LCMV)算法是一种较优的自适应数字波束合成算法，原理是在控制期望信号方向的增益为1、干扰方向的增益为0的前提下，使阵列输出功率最小[6]。其约束表达式为

CHW=f，

(3)

其中，C=[a(θ0),a(θ1)]为N× 2维约束矩阵；θ0为期望信号方向；θ1为干扰信号方向；f=[1,0]T为2 × 1维响应矩阵。

线性约束最小方差算法的数学表达为

min(WHRxW)，

(4)

s.tCHW=f，

(5)

其中，Rx为接收信号(期望信号、干扰和噪声)的协方差矩阵。

利用拉格朗日乘子法解得最优权矢量Wopt为

Wopt=Rx-1C[CHRx-1C]-1f.

(6)

由于系统幅相误差的存在，使接收到的信号的协方差矩阵Rx和实际信号的协方差矩阵Rrx存在差异，算法的性能也因此下降。Rx的误差也就是期望信号的误差和干扰的误差，为了减少误差的影响，对Rx做一个预处理，线性约束最小方差算法是在期望信号响应为1的情况下，使期望信号、干扰、噪声的功率最小，也就是使干扰和噪声的功率最小。所以，在Rx中减去期望信号的成分：

Xi+n=Xx-Xs,

(7)

(8)

其中，Xx为接收到的信号(期望信号、干扰和噪声)；Xs为接收到的期望信号；Xi+n为接收到的干扰加噪声；Ri+n为仅含干扰加噪声的协方差矩阵。那么最优权矢量变为

Wopt0=Ri+n-1C[CHRi+n-1C]-1f.

(9)

这样，接收到的信号的协方差矩阵Rx和实际信号的协方差矩阵Rrx的误差就是接收到的干扰和实际的干扰之间的误差。

4.3 MATLAB实验仿真与结果分析

对于行星际闪烁望远镜主站的抛物柱面天线，单个柱面天线包含304个馈源，馈源间距为半波长。在行星际闪烁观测中，需要对所有馈源的信号进行波束合成处理，实现天线指向不同的射电源。这里可以将所有馈源视为一个馈源线阵，阵元个数N=304个，阵元间距d=0.5λ。为了评估数字波束合成算法的性能，进行了如下仿真：

(1)假定期望信号到达角为10°。常规数字波束合成算法的阵列方向图如图5。

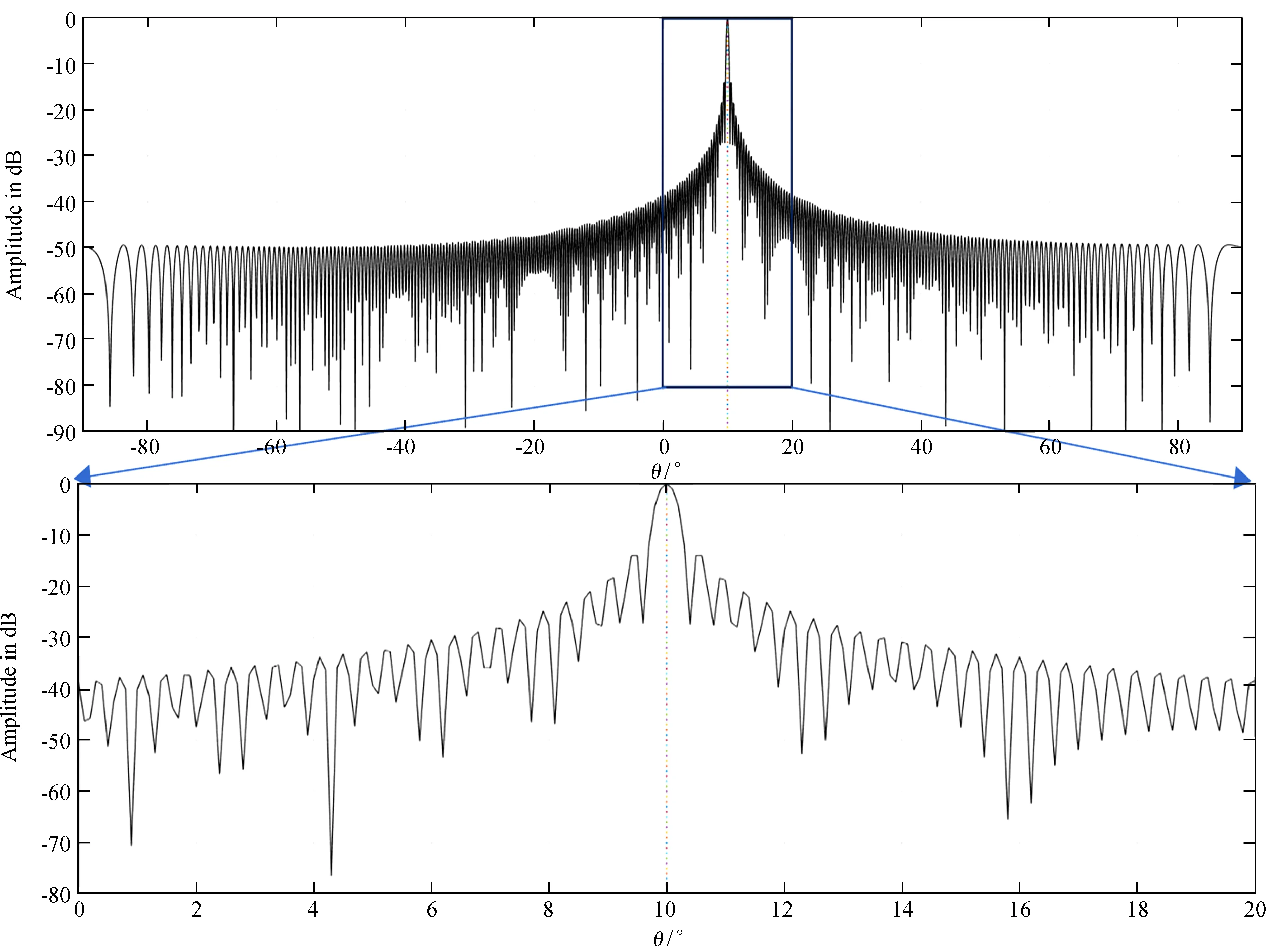
图5 常规波束合成算法形成的一个主波束

Fig.5 A main beam formed by conventional beamforming algorithms

(2)期望信号到达角为10°，干扰信号到达角为50°，快拍数为1 000，SNR=30 dB,INR=30 dB，干扰加上5%的幅相误差。基于线性约束最小方差算法的阵列方向图如图6。

仿真结果显示，线性约束最小方差算法可以抑制干扰，而常规波束合成算法不能抑制干扰。两种算法阵列方向图的第1旁瓣都较高，达到-13.4 dB左右，不满足行星际闪烁望远镜数字波束合成旁瓣-20 dB的技术指标要求(表1)。在观测中，干扰有可能从较高的旁瓣进入接收系统，影响观测结果。

5 改进的数字多波束合成算法

常规波束合成算法可以通过加窗的方法降低旁瓣以达到行星际闪烁望远镜技术指标[7]，但加窗的方法损失了天线的灵敏度。本文在线性约束最小方差算法的基础上提出了一种改进算法，在不损失天线灵敏度的情况下降低旁瓣，以满足行星际闪烁望远镜技术指标的要求。

5.1 改进的线性约束最小方差算法

线性约束最小方差算法在干扰信号方向形成深零陷，为此，采用设置虚拟干扰方法降低旁瓣。在线性约束最小方差算法结果中，寻找高于某个值(比如-25 dB)旁瓣峰值所在的角度，并将其设置为虚拟干扰信号方向。线性约束最小方差算法是让干扰信号的响应为0，即虚拟干扰方向深零陷，但这使得其他方向位置有较大升高。所以，改进算法让虚拟干扰响应不为0，而为一个很小的数，这样可以使虚拟干扰方向的旁瓣高度降低，但不会使虚拟干扰附近的部分旁瓣高度有较大升高。改进的线性约束最小方差算法的约束表达式可以表示为

C1HW1=f1，

(10)

其中，C1=[a(θ0),a(θ1),…,a(θm)]为N×(m+1)维约束矩阵；θ0位期望信号方向；θ1为干扰信号方向；θ2, …,θm为虚拟干扰方向；f1=[1,0,0.05,…,0.05]T为(m+1)×1维响应矩阵。改进的线性约束最小方差算法的数学表示为

min(W1HRxW1)，

(11)

s.tC1HW1=f1.

(12)

利用拉格朗日乘子法解得最优权矢量为

Wopt1=Rx-1C1[C1HRx-1C1]-1f1.

(13)

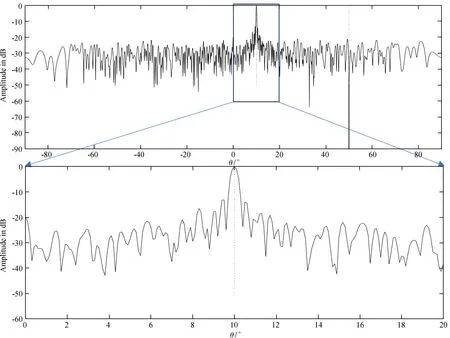
图6 线性约束最小方差算法形成的一个主波束

Fig.6 A main beam formed by LCMV algorithms

5.2 MATLAB实验仿真与结果分析

在同样的条件下，假定期望信号到达角为10°，干扰信号到达角为50°，快拍数为1 000，SNR=30 dB,INR=30 dB，干扰加上5%的幅相误差。将高于-25 db的角度设置为虚拟干扰方向。采用改进的线性约束最小方差算法，仿真结果如图7。

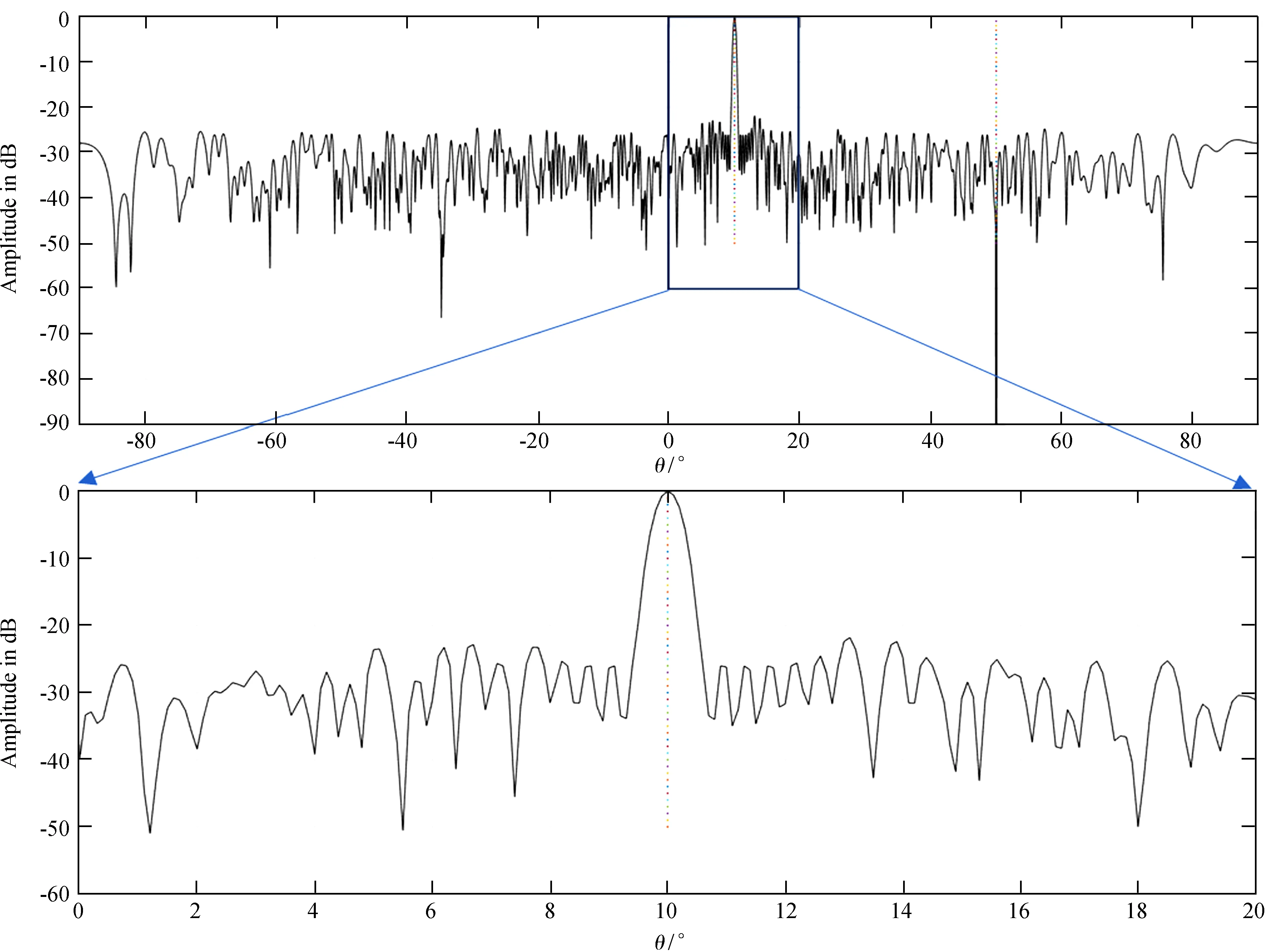
图7 改进的线性约束最小方差算法形成的一个主波束

Fig.7 A main beam formed by improved LCMV algorithms

仿真采用了改进的线性约束最小方差算法，将线性约束最小方差算法的阵列方向图中高于-25 dB的角度设置为虚拟干扰方向，并让其响应为0.05。仿真结果可以看出，阵列方向图主瓣附近高于-25 dB的旁瓣高度降低至-25 dB以下。由于增加了虚拟干扰方向响应的约束条件，虚拟干扰方向附近的部分旁瓣的幅度有小幅增加，超过-25 dB，但没有超过-20 dB。因此，改进后的线性约束最小方差算法达到了行星际闪烁望远镜的技术指标(-20 dB)要求。

6 基于子阵的改进数字波束合成算法

6.1 子阵化

如果对阵列的每个阵元都对应一个接收通道，这时阵列的响应最好，阵列控制波束指向的灵活度也最高。但是，对于本文这种大型阵列权矢量的维度很高，进而数字波束合成算法的复杂度很高，同时每个接收通道需要连接模数转换器、滤波器等硬件资源，系统非常复杂，硬件成本也很高。因此，在尽可能保持良好的阵列响应前提下，通过减少通道数的方式降低系统复杂度和硬件成本。采用子阵化方法减少通道数，每个子阵对应一个接收通道[8]。因此，提出基于子阵的数字波束合成算法，原理框图如图8。

表2是阵元级和子阵级的复杂度对比，可以看出，采用基于子阵的数字波束合成算法，除了子阵内阵元之间需要加多个模拟移相器外，在模数转换器个数、数据速率、权矢量维度都降低为原阵列的子阵内阵元的个数分之一。单个子阵内的阵元数目越多，模数转换器个数、数据速率、权矢量维度降低的越多，但是阵列控制波束的灵活度有所降低。所以，为了保持良好的阵列响应，不能一味地增加子阵内阵元的个数。

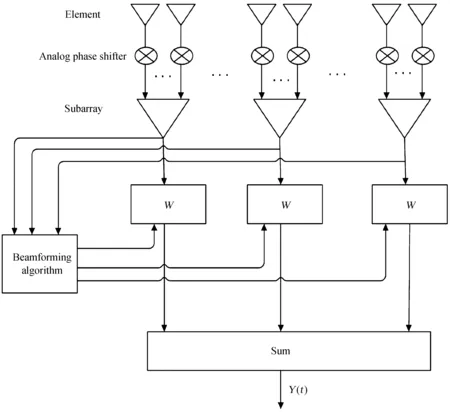
图8 基于子阵的数字多波束合成算法原理框图

Fig.8 Principle Block diagram of digital multi-beam beamforming algorithm based on subarray

表2 阵元级和子阵级复杂度对比

6.2 MATLAB实验仿真与结果分析

(1)对于由304个阵元构成的线阵，假定子阵阵元数分别为19、38，子阵间无重叠，期望信号到达角为10°，干扰到达角为50°，快拍数为1 000，SNR=30 dB,INR=30 dB，干扰加上5%的幅相误差。将高于-25 dB的角度设置为虚拟干扰方向。阵元之间采用移相器，使同一子阵内阵元相位为同相。子阵之间选用改进的线性约束最小方差算法。对子阵内不同阵元数分别进行仿真，仿真结果如图9、图10。

仿真结果显示，基于子阵(单个子阵内19阵元和38阵元)的改进线性约束最小方差算法满足了行星际闪烁望远镜的旁瓣指标要求，算法的复杂度相比阵元级数字波束合成算法大大降低。但是，以38个阵元为一个子阵的波束合成算法在干扰方向并没有形成深零陷，且第1旁瓣的幅度比较高，算法的性能明显降低。还对基于子阵(子阵阵元数分别为2、4、8、16)的改进线性约束最小方差算法进行了仿真，仿真结果满足行星际闪烁望远镜的旁瓣指标要求。而且，随着单个子阵阵元数的增加，算法性能会越来越低。因此，在可以整除304的数字中，19为最大的单个子阵阵元数。

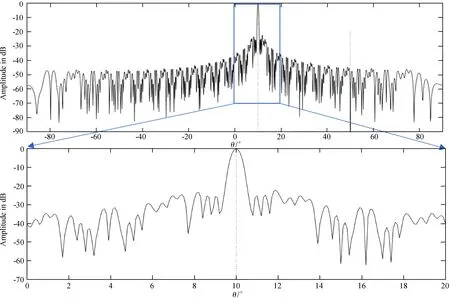
图9 基于子阵(19阵元)的改进线性约束最小方差算法形成的一个主波束

Fig.9 A main beam formed by improved LCMV algorithm based on subarray (19 elements)

图10 基于子阵(38阵元)的改进线性约束最小方差算法形成的一个主波束

Fig.10 A main beam formed by improved LCMV algorithm based on subarray (38 elements)

7 多波束合成

7.1 多波束合成原理

前面主要讨论了单个波束的合成，要同时对多个射电源进行观测，就需要形成多个主波束。要形成多个主波束，根据波束合成原理可知，阵列的权值决定了阵列方向图主波束的波束指向。因此，需要产生多组不同的权值。每组权值对应不同的相位补偿和幅度调整值，从而形成多个主波束[9-10]。合成多波束的原理框图如图11。

图11 多波束合成的原理框图

7.2 MATLAB实验仿真与结果分析

(1)仿真条件：阵元个数N=304个，阵元间距d=0.5λ，19个阵元为一个子阵无重叠，多个期望信号到达角为分别为-20°、0°、10°、30°，干扰信号到达角为50°，快拍数为1 000，SNR=30 dB,INR=30 dB，干扰加上5%的幅相误差。将高于-25 db的角度设置为虚拟干扰方向。阵元之间采用移相器，使同一子阵内阵元相位为同相，子阵之间选用改进的线性约束最小方差算法。仿真结果如图12。

图12 基于子阵(19阵元)的改进线性约束最小方差算法形成的4个主波束

Fig.12 Four main beams formed by improved LCMV algorithm based on sub-array (19elements)

由图12可知，在-20°、0°、10°、30°4个方向形成了主波束，且旁瓣基本达到了行星际闪烁望远镜技术指标。

8 总 结

本文对子午二期行星际闪烁望远镜的关键技术——数字波束合成技术进行了研究，提出了一种适应于行星际闪烁望远镜的柱面天线的数字波束合成算法。该算法在线性约束最小方差算法的基础上利用设置虚拟干扰的方法获得了满足行星际闪烁望远镜的合成波束。同时，采用子阵化的方法降低系统数字波束合成算法的复杂度，进而降低了工程实现难度。最后，在单个波束的基础上，提出了多波束合成算法，实现对天空多个射电源同时进行观测。