基于小批量K均值预分类的多波束反向散射强度角度影响改正

韩 冰，冯成凯，印 萍，梅 赛，张 凯，阳凡林,3

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266590；2.青岛海洋地质研究所，山东 青岛 266071；3.自然资源部海洋测绘重点实验室，山东 青岛 266590)

多波束声呐(multi-beam echosounder，MBES)作为海洋测量的重要手段，具有高效、稳定、准确等突出优点，广泛应用于海底地形地貌测量、海洋地质调查、海洋环境调查等诸多领域[1-2]。多波束声呐系统以条带测量方式实现海底全覆盖测量，在获得水下地形地貌的同时还可获得高分辨率海底声呐图像，为测区大范围海底底质分类、海底目标探测提供了可靠技术支撑。由于海洋环境以及声呐系统本身的复杂性，声信号在传播过程中受到海水吸收、声信号扩展、海底地形起伏、环境噪声和海底混响等影响。随着声学理论及散射理论的日趋完善，对于上述影响因素基本都可去除或削弱[3]。受声散射模型机理影响，不同入射角度下的回波强度不同，称为角度响应(angular response，AR)[2,4-5]。由于波束的实际入射角直接影响AR曲线形状，AR改正前需考虑换能器安装偏差、声线弯曲、地形起伏变化等因素的影响以建立严密的海底入射角计算模型[6-8]。

目前，国内外诸多学者已开展对AR模型及改进模型的研究。现有的AR模型建立方法主要有声学模型法和数学统计法，声学模型法主要是通过声散射公式推导反向散射强度与入射角的关系，进而建立散射理论模型，目前主要有Lambert模型[9-10]、Jackson模型[11]、Hellequin综合声学模型[12]等；数学统计法通过统计反向散射强度随不同入射角的变化规律而建立AR数学模型，主要有高斯拟合模型[13]、二次微分AR模型[3]等。前者虽考虑声散射机理，但只是近似模型，不能够准确描述不同仪器设备、复杂海洋环境下的角度响应，改正入射角效应时也引入了模型误差；后者通过数学统计来描述角度响应曲线，但在底质变化复杂的区域，角度响应曲线会发生突变，AR改正时会引起声呐图像局部异常。

为此，通过研究上述问题的成因，提出一种基于海底点预分类的反向散射强度AR改正方法，以期提高多波束声呐成图质量。

1 多波束声散射原理

多波束换能器能通过波束导向向海底发射并接收获得一系列波束，得到不同强度的波束回波信号。如图1所示，声波到达海底后，只有在特定方向发生声反射，剩余部分声能量将在海底发生散射和折射，其中只有少部分反向散射能量被换能器接收(通常为-10～-40 dB)[14]。经过系统改正后，回波强度除与海底入射角相关外，还与声波频率、海底底质类型等因素相关[3]。海底粗糙度影响海底声散射过程，当粗糙度大于波长时，海底回波强度与频率无关；当海底粗糙度中有部分小于波长时，海底回波强度随频率增加，声波频率效应对海底回波强度的影响需预先去除[1]。通过对实测数据统计发现，泥质海底的固有反向散射强度为-19.7 dB，砂质海底为-20.2 dB，沙砾海底为-11.7 dB，岩石海底为-5.6 dB[1]，其中岩石、沙砾等为高阻抗平滑底质，对声波有较强的散射性；细沙、泥质等为低阻抗粗糙底质会吸收较多的声能量，表现为较弱的散射回波[14]。

对于小入射角，回波信号主要为反射回波，且包含较多噪声干扰[15]，称为小入射角区(D1区)；随入射角的增加，回波信号主要来自海底底质的反向散射回波，称为漫发射区(D2区)；D2区之外的大入射角区域，回波强度随入射角表现为线性相关，称为高入射角区(D3区)[16]。

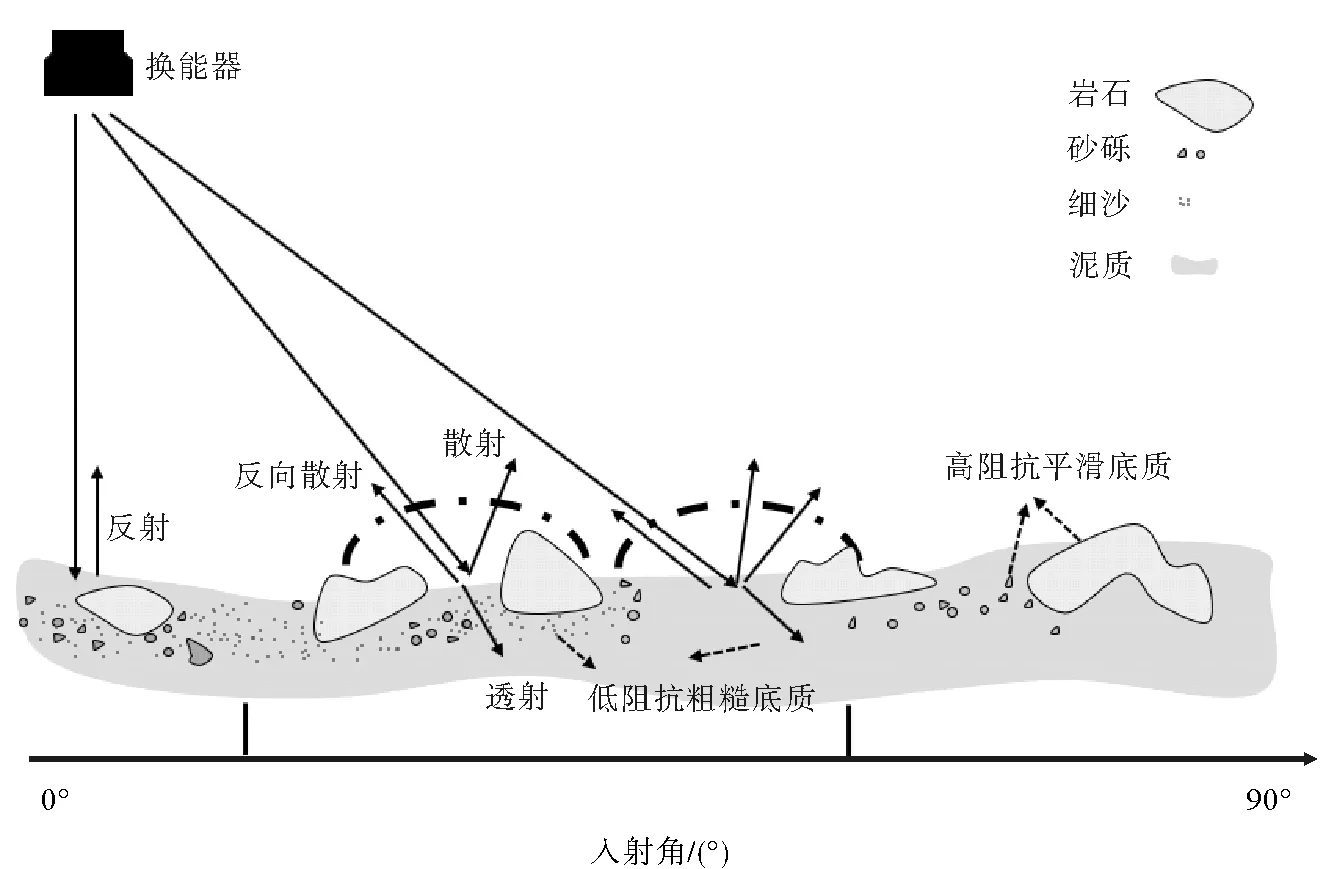
图1 海底声散射示意图

图2 本文方法流程图

2 基于预分类的多波束AR改正

准确获取反向散射强度图像是进行底质分类和声呐图像判读的基础。在进行AR改正时，发现声呐图像局部条纹和拼接异常通常发生在高阻抗平滑底质和低阻抗粗糙底质的交界处。这是由于高阻抗平滑底质和低阻抗粗糙底质反向散射强度相差在10 dB以上，在利用传统方法进行统计和AR建模时会因为角度响应曲线突变造成模型误差。因此，如何在AR改正前对高阻抗平滑底质和低阻抗粗糙底质进行区分成为关键问题。为方便描述，将高阻抗平滑底质称为硬底质，低阻抗粗糙底质称为软底质。首先，利用小批量K均值(mini batch K-means)聚类算法[17]对强度预处理后的海底点预分类为硬底质点和软底质点。在已知海底硬底质点和软底质点分布的前提下，考虑局部海底底质变化且避免偶然误差的影响，对连续多次声脉冲(Ping)回波强度数据取均值获取其局部平均角度响应曲线。然后，对角度响应曲线进行小波分析去噪、峰值探测区域边界等步骤构建自适应AR改正模型。最后，去除反向散射回波信号的AR效应，通过地理编码准确地获取测区海底声呐图像。本文方法流程如图2所示，其中i为当前所处理的测线，n为所处理测线总数。

2.1 Mini batch K-means海底点聚类

为保证测区条带间聚类标准一致，应对所有测线海底点进行整体聚类。就浅水多波束系统而言，单条测线的海底点云数量可达100多万，整个测区点云数量则更为庞大，对于计算效率和计算机性能也是极大的考验。K-means算法计算复杂度低、聚类效果好，非常适于大型数据集的探索性聚类分析，但直接采用K-means算法对原始点云进行聚类时计算效率并不高。Sculley等[17-18]提出的mini batch K-means算法通过每次选取小批量数据进行K-means聚类，利用学习稀疏簇中心的方法，减小了计算耗时和存储开销。为避免角度因素对强度聚类的影响，聚类应在同角度间隔下进行，本mini batch K-means海底点聚类算法如下：

1) 初始化：海底点强度样本按等角度间隔α划分为子样本Iu(u=1,2,3…)，聚类簇数g=2，最大迭代次数M，记每个类别的样本数量为：N1,N2,…,Nk，样本总数为N，mini batch个数b=1 000，中心计数v=0。

2) 从子样本Iu中随机选取g个样本点作为初始的强度聚类中心点:{μ1,μ2,…,μj}。

3) 从子样本中Iu中随机选取b个海底点。

4) 计算样本点bi到各聚类中心的距离

(1)

5) 利用梯度下降法，对每个样本点bi(i=1,2,…,b)对应的最近聚类中心μj(j=1,2,…,g)据式(2)～(4)进行更新：

v[μj]=v[μj]+1，

(2)

(3)

μj=(1-η)μj+ηbi。

(4)

6) 重复3)～5)步，直至达到最大迭代次数，则子样本Iu聚类结束。

7) 所有子样本Iu完成聚类，输出聚类结果。

2.2 反向散射强度AR改正

多波束反向散射强度同时受入射角和底质类型的影响。2.1节中算法可将海底点区分为硬底质点和软底质点，但岩石和沙砾等虽同属硬底质，其AR曲线也表现出细微差别，为更好地顾及海底局部底质变化，本研究分别针对硬底质点和软底质点前后连续100 Ping作为滑动窗口，对同角度下反向散射强度取均值获取平均AR曲线。

2.2.1 AR曲线小波去噪

平均AR曲线可以较好地表达反向散射强度随入射角的变化趋势，然而实际曲线中局部仍有较小的波动，特别表现在受反射影响较大的小入射角区(D1)[15]，为消除偶然误差及粗差的影响，需要对曲线进行去噪平滑处理。

离散小波变换(digital signal processing，DWT)可通过小波基的尺度变换和位移对原始信号进行多尺度和多分辨率的探测，进而通过时频域转换去除信号中的高频干扰。

(5)

其中，x(t)为待处理的平均强度序列，ψj,k表示母小波，j为缩放因子，k为平移参数。

Daubechies小波[19]为离散正交小波(简写为dbN，N是小波的阶数)，具有时域、频域局部处理能力，常用于信号去噪分析。dbN没有明确的表达式，但转换函数h的平方模是明确的。选取db4小波基对平均角度响应曲线进行n层分解得到信号低频系数和高频系数，然后通过逐层去除分解后的高频系数进行平滑处理。如果分解层数过多，则曲线过于平滑，不利于边界角的提取，如果分解层数较少，则会干扰边界的提取。图3为不同分解层数下的平均AR曲线小波去噪效果，通过对比分析发现，当n=3时曲线已经足够平滑，n>3时会过平滑，则n=3即为最优分解层数。最后通过分解系数波形重构，可得到准确的AR曲线。

图3 不同分解层数下的平均角度响应曲线小波去噪效果

2.2.2 AR曲线边界提取

对去噪后的平均AR曲线可采用峰值探测法快速获得分区边界[20]。经验数据表明D1～D2区的边界角在10°～35°之间，D2～D3区的边界角在40°～60°之间，两边界角位置对应的强度值均为局部极小值，因此可在上述两角度区间内对平滑后的平均强度序列提取局部极小值点。极小值点处对应的入射角为：

θ=A(find(diff(sign(diff(BS)))<0)+1)。

(6)

其中：BS为平均强度序列，A为对应的角度序列，diff为差分运算，sign为符号函数，find指查找满足条件的序列号。

由于随机误差及复杂底质的影响，在两角度区间内可能存在多个局部极小值点，因此须将极小值点进行筛选。如图4所示，Port表示左舷，Starboard表示右舷，在10°～35°区间，AR曲线在小入射角区呈大斜率变化，在漫反射区大致符合Lambert法则，通过计算两相邻局部极小值点的斜率k，其中k发生突变的点对应的角度θD1～D2即为D1～D2区边界角；在40°～60°区间，对获得的局部极小值进行排序，其中最小值对应的角度θD2～D3即为D2～D3区边界角。为平稳过渡D1、D2区，还应在θD1～D2左右一定范围内设立过渡区D1,2。

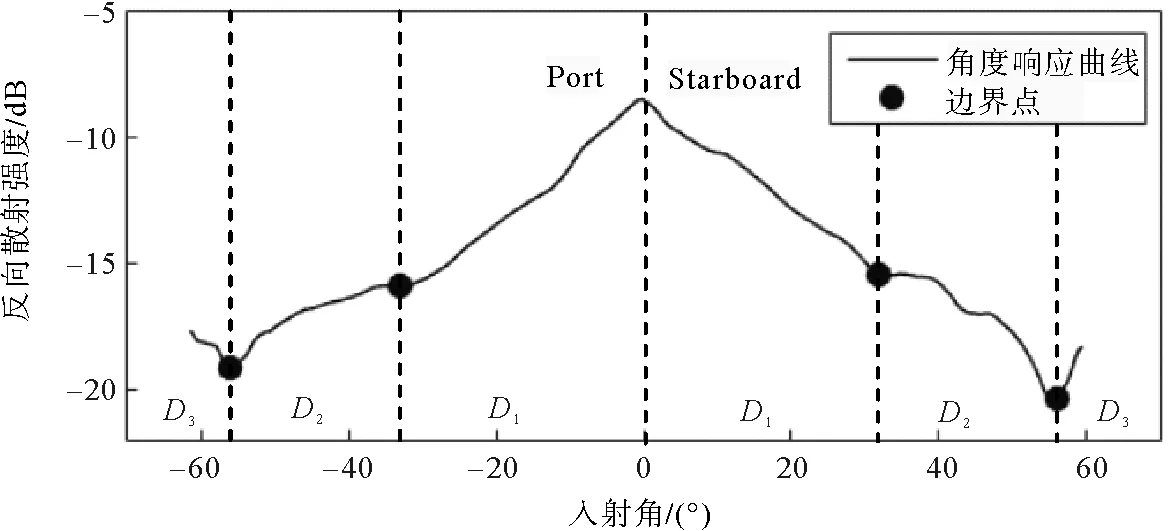
图4 峰值探测法多波束角度响应曲线边界角提取

2.2.3 AR自适应模型构建

从图4可以看出，真实的AR曲线并不完全服从传统Lambert法则模型，且在不同的区域表现为不同的曲线类型。为了克服Lambert法则模型存在的不足，针对三个主要分区及过渡区的特点，依据2.1节中提取的区域边界，并综合二次微分AR模型给出改进的自适应AR模型：

(7)

k=k2-[10lg(cos2θ2)-10lg(cos2θ1R)]/(θ2-θ1R) 。

(8)

式(7)～(8)中，θ为波束海底入射角；BSi(i=1,2,3)为Di区的起始强度值；θi为分区边界角，θ1L和θ1R为过渡区边界角；ki(i=1，2，3)为Di区的平均斜率，可由平均角度响应曲线离散点序列线性回归求取；k为D2区的补偿斜率，用于补偿自适应AR模型与Lambert法则之间的的差值；fit函数为过渡区拟合函数，本研究选取三次多项式拟合函数；BSm为自适应AR模型值。

2.2.4 AR影响去除

对于中国农民而言，“纠纷宝塔理论”所刻画的由下至上的纠纷解决层级结构并非是一个需要“攀爬”的实体[14]，而是一个可以灵活选择而跳跃达至的扁平结构。乡土正义系统是纠纷解决过程中以农民的法律资源选择为主的法律秩序公共品集合体。就本文的分析所及，乡土正义供给系统看似具有层级性，但在农民进行法律资源选择的过程中，正义系统中的部件结构却是扁平化的，农民既可以找村干部调解纠纷，也可以向派出所寻求帮助，也可以综合利用乡镇政府的熟人关系网络来促成纠纷的解决。

2.2.3节中给出自适应AR模型可以很好地表达不同入射角下反向散射强度的变化规律，因此要去除AR的影响，可针对单Ping的反向散射强度减去自适应AR模型值。为获得底质的真实反向散射强度，应再加上左右舷波束在漫反射区(D2区)的平均回波强度[13]，海底点真实强度值由式(9)～(10)计算。

BSn=BS-BSm+BSmean，

(9)

BSmean=(BSport+BSstarbord)/2。

(10)

其中，BSn为AR改正后反向散射强度值，BS为AR改正前反向散射强度，BSm为AR模型值，BSmean为底质在漫反射区的平均回波强度，BSport与BSstarboard分别为左、右舷波束漫发射区平均强度。

图5 海底预分类效果图

3 实验与分析

为验证本文算法，选取2016年4月于浙江舟山某海域实测多波束数据进行分析，选取4条相邻测线来说明。测量采用R2Sonic2024多波束测深系统，波束开角120°，声呐频率400 KHz，波束个数256个，测区位于长江入海口,水深20～30 m，海底底质较为复杂，原始数据已进行传播损失、声呐参数、声照区面积等改正，经上述步骤改正后的回波强度主要受AR效应的影响。

3.1 实验结果

3.1.1 预分类结果

将预处理后的海底点按照其强度属性进行mini batch K-means聚类，4条测线上共计海底点487万个，聚类簇数为2，为保证分类准确率，设置角度间隔α=1°，迭代次数为500次，聚类总耗时10.03 s。图5为海底点预分类效果图，其中图5(a)为经过地理编码的AR改正前海底声呐图像，图5(b)为经噪点剔除及地理编码的软、硬底质分布图，通过对两图分析可以发现，本文算法可以有效区分软、硬海底底质，且分界明显、自然，可见本mini batch K-means算法对于数据量庞大的海底点预分类具有可行性。

3.1.2 AR改正结果

从图5(a)可以看出，角度响应对回波强度有较大影响，很难直接对AR改正前的声呐图像进行海底目标判别和底质分类。在预分类完成后，针对每条测线逐类进行AR改正。为便于比较，选取Lambert模型法、二次微分法与本文方法改正结果进行分析。对改正后的4条测线进行地理编码，拼接后的测区海底声呐图如图6所示。利用Lambert模型法改正(图6(a))后，一定程度上去除了AR，但测线重叠区有明显拼接痕迹，图像整体较为模糊；二次微分法改正(图6(b))后测线整体散射强度较为均衡，而从图中仍可看到测线边缘痕迹；本文方法改正(图6(c))后，有效去除了AR，测区整体图像清晰，测线过渡自然。

图6 不同方法改正效果比对

3.2 讨论与分析

最大信息系数(maximal information coefficient，MIC)[20]可以很好地检测变量之间的非线性相关性，MIC值越接近0，说明反向散射强度与入射角的相关性越小，AR去除效果越好。通过与其他方法比较发现，本文方法MIC值最小，为0.123，说明本文方法AR去除效果最佳。为直观表达，选取底质均一的相同区域20 Ping数据绘制强度散点图，拟合其趋势线，结果如图8所示。

图7 不同方法改正局部(图6方框)效果比对

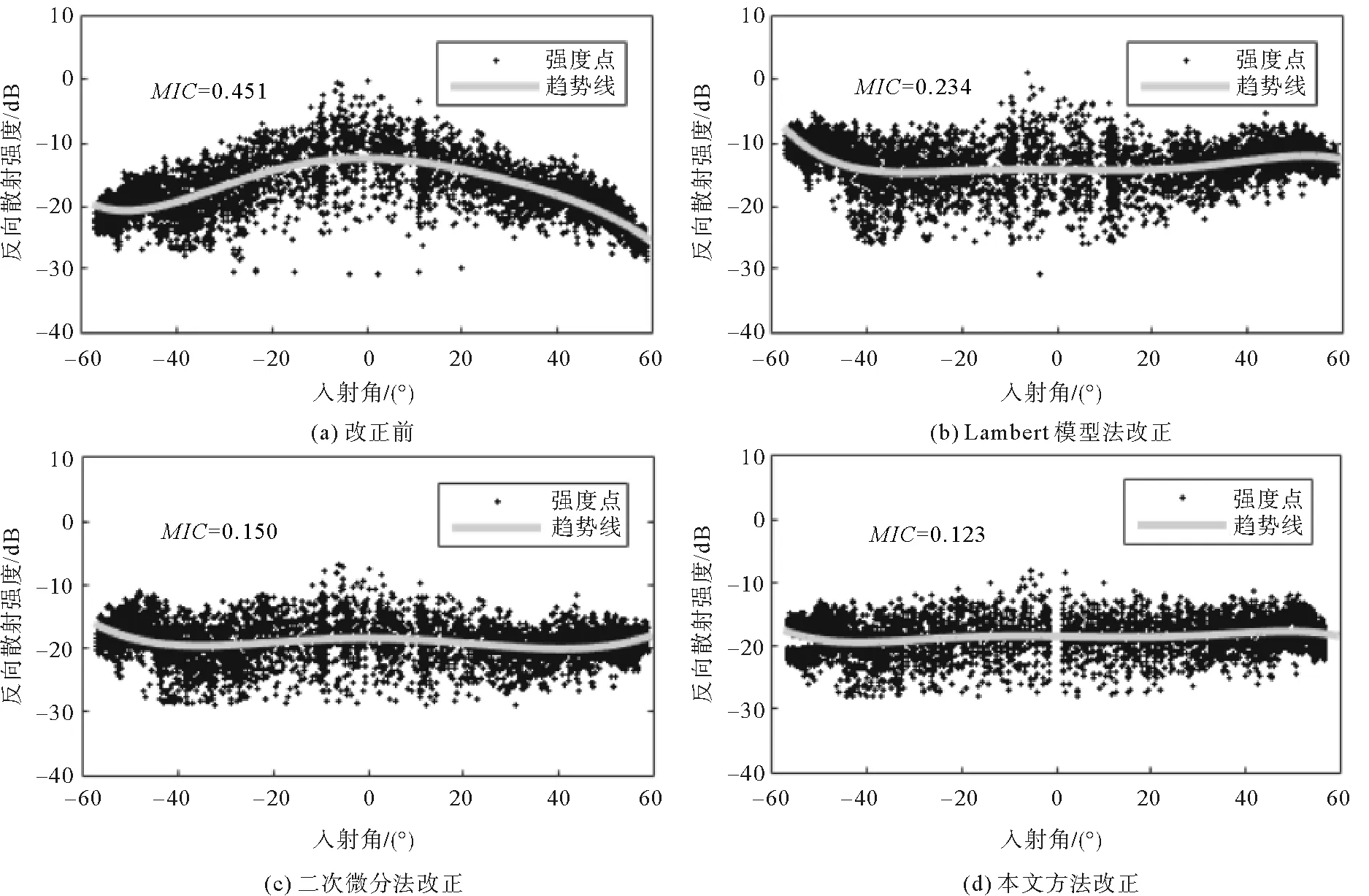
图8 不同方法的AR去除效果

从图8可以看出，三种方法均在一定程度上去除了角度响应的影响。由于Lambert模型边界角的固定性，改正时反而引入了一定的误差，其趋势线仍然呈一定弯曲；相较于Lambert模型法，二次微分法对于AR的去除较好；本文方法改正后趋势线基本呈直线，AR去除效果最好。

为进一步验证评估该算法条带拼接的一致性，选取4条测线的重叠区域进行分析。提取不同测线相同位置的回波强度差值，并统计其概率密度分布、均值和中误差如图9所示。

改正前测线重叠区回波强度值均值存在明显的系统偏差，均值为-0.63 dB，标准差为5.48 dB；经Lambert模型法改正后系统偏差得到了修正，均值为-0.22 dB，但其标准差仍然较大，为3.32 dB；二次微分法改正后均值为0.73 dB，标准差有进一步改善，为1.83 dB；本文方法改正后重叠区强度差值概率分布峰值出现在0附近，均值为0.22 dB，基本符合正态分布，标准差为1.46 dB，较其他方法最小，进一步证明了本文方法的有效性。

图9 测线重叠区强度差值概率密度分布

4 结论

基于声散射理论研究并分析现有多波束AR改正模型的不足，提出了基于预分类的反向散射强度AR改正方法。通过对回波强度固有属性差别较大的硬底质和软底质进行预分类，保证了复杂海底底质环境下多波束AR曲线的准确提取，同时提高了测线间回波强度水平的一致性；利用小波函数进行角度响应曲线去噪，削弱了偶然误差和粗差对角度响应曲线的影响；峰值探测法提取边界角以及自适应AR模型的构建，实现回波强度AR效应的去除。

选取浙江舟山海域实测4条相邻测线进行分析，并采用Lambert模型法、二次微分法与本文方法分别进行了反向散射强度角度响应去除。对比发现，本文方法处理后有效去除了多波束回波强度AR效应，角度因素与反向散射强度的相关性最小(MIC=0.123)，条带重叠区反向散射强度标准差为1.46 dB，较其他方法小。从海底声呐成像质量来看，本文方法处理后海底声呐图像清晰，不同底质分界明显，有效解决了复杂底质环境下声呐图像局部条纹和整体明暗不一的问题，为后续底质分类等工作奠定了基础。