基于岩性及结构特征的砂岩含水层富水性评价

2020-05-12魏久传赵智超谢道雷俞功一山

山东科技大学学报(自然科学版) 2020年3期

魏久传，赵智超，谢道雷，俞功一山，吴霞

(1.山东科技大学地球科学与工程学院，山东青岛 266590； 2.山东省煤田地质局物探测量队，山东济南 250104)

矿井水害是煤矿安全生产的重大威胁，其中煤层顶板砂岩水害是重要灾害类型之一。在我国各时代煤田中，可采煤层顶、底板往往广泛分布着砂岩含水层。在矿井建设和煤炭资源开采过程中，若井巷工程揭露或沟通砂岩含水层富水区域，可瞬间引发大量突水，轻者造成淹面淹头事故，重者可引发淹井甚至惨重的人员伤亡事故[1-2]。

在传统研究中，砂岩含水层富水性评价通常建立在大量物探、钻探、水文地质试验(抽水试验、放水试验等)基础之上。然而，在实际生产中，抽水钻孔数量一般较少，且控制范围有限，无法满足对含水层富水性分布规律的详细控制；物探方法如瞬变电磁法、直流电法等[3]存在工作量大、费用高等问题，且物探资料的多解性使得对富水区的解译成为难题，常出现谬误。因此，借助大量现有地质勘查钻孔资料，充分利用数据综合分析方法，提取煤层顶板岩性特征及分布规律等信息，分析含水层富水性，是一种简便有效的方法。我国相关领域专家学者对含水层富水性的研究，主要通过对多指标求得权重来构建富水性模型，如：武强等[4]选取含水层厚度、脆塑性岩厚度比、单位涌水量、岩石质量指标、渗透系数、冲洗液消耗量、断层、陷落柱、褶皱枢纽轴等9个指标，运用层次分析法确定权重构建富水性评价模型；武旭仁等[5]运用模糊聚类分析法构建含有砂岩厚度、砂泥比和断层维数3个指标的评价体系；李哲等[6]选取含水层厚度、岩芯采取率、脆性岩厚度、风化影响指数作为评价指标，应用人工神经网络得出富水性评价模型。数据综合分析法中关于权重的确定常选取单一方法，其中主观赋权法重视各指标本身的含义，可以体现决策者对不同指标的重视程度，但客观性较差；而客观赋权法具有较强的数学理论依据，但缺少决策者的参与和对实际情况的考虑。

本研究结合典型实例，遵循客观科学性、全面性、定量与定性分析相结合的原则，运用熵权系数法、主成分分析法和层次分析法，选取砂岩等效厚度等多个评价指标，确定综合权重并构建预测模型，对砂岩含水层的富水性进行预测分区，为防治顶板水害提供依据。

1 研究区概况

研究区位于内蒙古自治区鄂尔多斯市西南部的乌审旗境内(图1)，内部构造活动较为微弱，构造不发育，含煤地层为侏罗系中下统延安组，讨论的22采区2煤层可采厚度5.86～8.03 m，平均厚度6.88 m。2煤上覆直罗组砂岩含水层、安定组隔水层和志丹群砂岩含水层，含隔水层结构如图2所示。安定组发育多层泥岩、砂质泥岩、粉砂岩等，其岩性较致密，透水性能差，为相对隔水层。因此，2煤顶板直罗组砂岩含水层、志丹群砂岩含水层为影响2煤开采的主要含水层。

2 含水层富水性因素分析

2.1 富水因素的确定

研究区营盘壕煤矿处于鄂尔多斯盆地中部，内部构造活动较弱，构造不发育，沉积环境是控制该地区地层中含(隔)水层空间分布与含水层富水规律的主要因素，因此在指标的选取中主要考虑岩性对富水性的影响。选取砂岩等效厚度(M)、砂岩岩性系数(S)、岩芯采取率(P)、砂泥岩层比率(Q)4个因素作为研究区富水性分区评价指标，对煤层顶板砂岩含水层的富水性做出预测。

图1 研究区位置示意图

图2 含、隔水层结构示意图

1) 砂岩等效厚度(M)

砂岩厚度作为含水层富水性评价的主要指标之一[7-8]，其厚度越大富水性越强。然而在已有的富水性评价研究中，砂岩厚度往往仅将含水层内不同砂岩厚度简单相加，而忽略了粗、中、细砂岩的孔隙度及渗透性差异，结果往往与实际有较大出入。本研究引入砂岩的等效厚度(M)，将砂岩孔隙度比值作为不同砂岩厚度换算的比例系数，乘以各类砂岩的真实厚度得到砂岩等效厚度，具体公式为：

M=M粗+k1M中+k2M细，

(1)

其中：M粗、M中、M细分别为粗砂岩、中砂岩、细砂岩的真实厚度，m；k1为中砂岩厚度换算等效系数；k2为细砂岩厚度换算等效系数。

本研究按照覆压下岩石孔隙度和渗透率测定方法(SY/T 6385—1999)标准对研究区直罗组不同层段岩芯进行了测试(表1)，并以粗砂岩为基础(设定为1)，折算中、细砂岩对粗砂岩厚度换算的等效系数。结果显示k1=0.8，k2=0.7。

表1 2煤顶板直罗组岩层孔隙度统计分析表

2) 砂岩岩性系数(S)

砂岩岩性系数(S)是砂岩的实际厚度与研究范围直罗组厚度的比值，该比值越大，说明该段岩层中砂岩占比越高，富水性越强。

3) 岩芯采取率(P)

岩层的孔隙、裂隙为地下水的赋存提供了重要空间，选取岩芯采取率(P)能够直观地反映岩体完整程度，了解裂隙发育程度。岩芯采取率越高，说明岩层越完整，其中裂隙发育的就越少，富水性就越弱，故岩芯采取率和富水性成负相关。

4) 砂泥岩层比率(Q)

砂-泥岩的组合特征直接影响含水层的渗透性，砂泥互层越多，隔水性能越好，然而，单层砂岩或者泥岩厚度也对富水性有显著影响，为克服这一局限性，提出砂泥岩层比率这一评价指标，即一定岩层厚度范围内，砂质岩层和泥质岩层的总层数与该组地层厚度的比值，本文将每10 m岩层中的砂泥互层数定义为砂泥岩层比率，该值越大，表明隔水能力越强，富水性越弱。

2.2 数据标准化

文中确定的影响含水层富水性的指标具有不同的量纲，为了使数据之间具有可比性和客观性，对原始数据进行标准化处理，采用的极差标准化公式为：

(2)

其中：X为该指标原始数值；Xmax、Xmin分别为该指标原始数据中的最大、最小值，Xi为该指标标准化结果值。

原始数据经过标准化后的结果见表2。各指标标准化后单因素专题图如图3所示。

表2 直罗组含水层富水性各影响因素数据标准化值汇总表

图3 直罗组含水层富水性评价单因素评价专题图

3 评价指标权重确定

熵权系数法确定权系数具有客观性强、数学理论完善等优点，但评价指标之间可能存在一定的相关性；主成分分析能够有效消除样本中冗余的信息，但在变量降维的过程中不得不付出使变量带有模糊性的代价；层次分析法能够将对象视作一个系统，使定性与定量相结合，可以将专家针对不同开采地质条件下的分析经验应用到评价中。三种方法的结合，可以减少单一评价方法对某一指标权重的绝对影响，削弱或消除单一方法的弊端。经试算比较，将三种计算方法相结合能够提高计算结果的准确度。

3.1 熵权系数法确定权重

熵权系数法(entropy weight method，EWM)的基本思路是根据指标变异性的大小来确定客观权重，熵值越小，变异程度越大，权重也就越大[9]。具体步骤如下：

1) 求各指标的信息熵

根据信息论中信息熵的定义，一组数据的熵值为

(3)

其中

(4)

2) 确定各指标权重

根据信息熵的计算公式，计算出各个指标的信息熵为H1,H2,…,Hm。通过信息熵计算各指标的权重：

(5)

计算4个评价指标M、S、P、Q的权重并进行归一化处理，得到权重结果分别为0.353 4、0.258 3、0.022 1、0.366 2。

3.2 主成分分析法确定权重

主成分分析法(principal component analysis，PCA)是将原有变量重新组合生成少数几个彼此不相关的变量即主成分，使它们尽可能多地提取原有变量的信息[10-11]。通常做线性组合使原变量重新组合成主成分：

(6)

其中：a1i，a2i，…，api(i=1，2，…，m)为X的协方差阵特征值对应的特征向量；X1，X2，…，Xp是原始数据经过标准化的值。

评价因子的权重，数学表达式如式(7)所示。

(7)

其中，gq为第q主成分的方差贡献率，aqi(q=1,2,…,m;)为i因子在q主成分中的系数，所求的wi为第i个指标的权重值。

利用SPSS软件对数据进行分析，结果见表3和表4。

按照主成分特征值大于1选取成分1(F1)和成分2(F2)两个主成分，其累积贡献率分别是50.887%，83.770%(表3)。

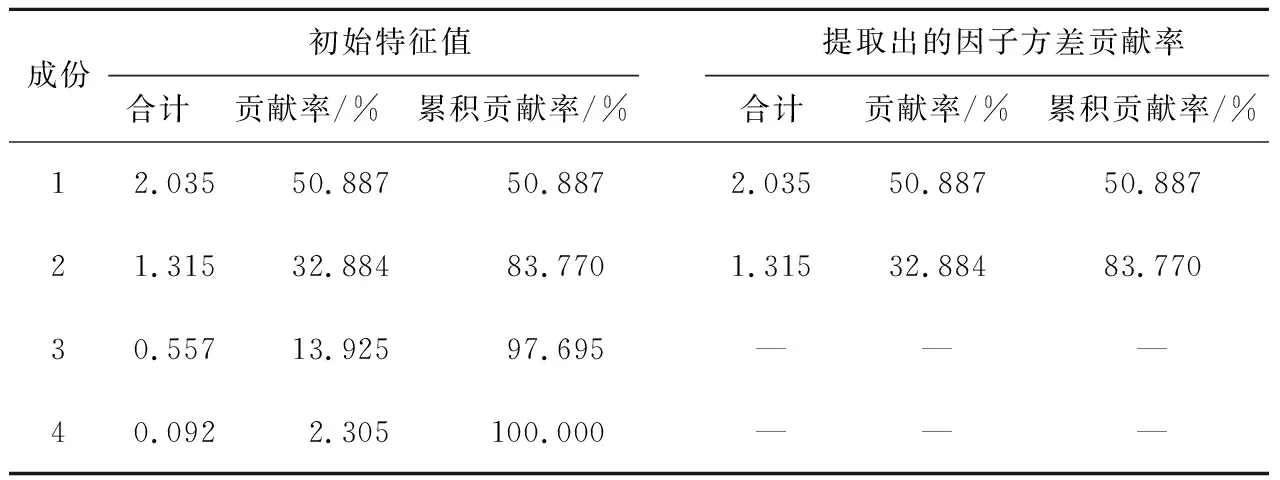
表3 主成分贡献率与累积贡献率 Tab. 3 Principal component contribution rate and cumulative contribution rate

表4 成份得分系数矩阵

根据表3和式(6)得到主成分表达式：

F1=0.470M+0.475S-0.151P+0.150Q，

(8)

F2=0.047M-0.059S+0.626P+0.601Q。

(9)

根据式(7)，主成分所求权重w1=|0.470×50.887%+0.047×32.884%|=0.254 6，同理可得w2=0.222 3,w3=0.129 0,w4=0.274 0。归一化后得4个评价指标M、S、P、Q的权重分别为0.289 4、0.252 7、0.146 6、0.311 4。

3.3 层次分析法确定权重

层次分析法(analytic hierarchy process，AHP)，是一种定量和定性相结合将决策问题分解为多准则、多目标、多指标的实用决策方法[12-14]。本研究借助专业层次分析软件yaahp确定各个影响指标的权重。

1) 建立层次结构模型

将决策目标、中间层要素、备选方案绘制层次结构图如图4。

图4 直罗组含水层富水性分析层次结构模型

2) 构造判别矩阵

依据Seaty等[15]提出的1～9标度法，根据各个评价指标对决策目标所起作用的大小进行两两比较，按重要程度评定等级，建立判别矩阵。例如：以研究对象A为目标，bi、bj(i，j=1，2，…，n)为第二层指标因素，bij代表了bi对bj的相对重要性，由此建立判别矩阵如式(10)、式(11)所示。

(10)

(11)

计算得4个评价指标M、S、P、Q的权重分别为0.221 7、0.351 8、0.093 1、0.333 4。

3) 确定各评价指标权重

将熵权系数法求得的权重w1、主成分分析法所得权重w2和层次分析法所得权重w3相结合确立综合权重w，在保证结果客观准确的前提下，结合实践经验，对各权重进行约束求得组合权重(见表5)。

(12)

其中：w为综合权重；n为影响因子个数。

表5 组合权重的计算

根据式(12)求得：

w=(0.288 1,0.287 6,0.087 3,0.337 0)。

(13)

4 富水性预测模型的建立及验证

4.1 富水性预测模型的建立

依据式(12)计算的组合权重得出直罗组砂岩含水层富水性预测模型为：

D直罗=0.288 1M+0.287 6S-0.087 3P-0.337 0Q。

(14)

其中，D代表组合权重所计算的富水性指数，M、S、P、Q代表每个指标标准化值。指标P、Q与富水性呈负相关关系，因此P、Q指标前取负号。

根据式(14)得到研究区各个钻孔的富水性指数，将富水性指数归一化处理，再利用surfer软件进行插值，统计得到富水性指数频数直方图(图5)，确定分区阈值(0.2，0.5，0.6)。

同样方法求得志丹群砂岩含水层富水性预测公式(15)，富水性指数频数直方图(图6)。

D志丹=0.334 6M+0.254 6S-0.092 9P-0.317 9Q。

(15)

图5 直罗组砂岩含水层富水性指数频数直方图

图6 志丹群砂岩含水层富水性指数频数直方图

4.2 结果及验证

钻孔抽水层位于直罗组的钻孔有K4-7、K4-9、X202、K8-4，单位涌水量q分别为：0.050 6、0.043 4、0.306 8、1.140 2 L/s·m。

根据《煤矿防治水细则》，含水层富水性依据钻孔单位涌水量q值进行等级划分，分为弱、中等、强和极强4个等级[16]。K4-7、K4-9钻孔单位涌水量小于0.1 L/s·m，为富水性弱区；X202钻孔单位涌水量区间为(0.1，1] L/s·m，为富水性中等区；K8-4钻孔单位涌水量大于区间为(1，5] L/s·m，为富水性强区。因此，将富水性评价指数(0，0.2]定为弱富水性区，将(0.2,0.5]定为中等富水性区，(0.5，0.6]和(0.6,1]区间合并定为富水性强区，即研究区内不存在富水性极强等级。绘制22采区2煤顶板直罗组砂岩含水层富水性分区图，如图7所示。

抽水层位位于志丹群的检3钻孔、ZD-1钻孔，单位涌水量分别是0.348、0.418 L/s·m。这两个钻孔均位于富水性中等区域，根据抽水试验结果对富水性进行分区，绘制22采区志丹群砂岩含水层富水性分区图如图8所示。

富水性评价结果表明，直罗组砂岩含水层在22采区西北部大部分地段、东北部部分地段的富水性弱，东部和中部大部分地段富水性中等，有小范围为富水性强区(图7)。志丹群砂岩含水层大部分属于富水性中等区域，西部、东南部富水性较强，东部和中部部分地段为弱富水性区(图8)。

图7 直罗组砂岩含水层富水性分区图

图8 志丹群砂岩含水层富水性分区图

4.3 分区结果差异对比与分析

基于传统单一主成分分析法得到的直罗组富水性分区图如图9所示，由图可知，两种方法所得结果总体相似，但由于赋值方法侧重不同，在局部区域分区结果方面存在一定差异，如：①研究区西南部，EWM-PCA-AHP三种方法结合分区结果表现为较大面积的中等富水区，而单一主成分分析法表现为弱富水区；②K4-6钻孔附近区域，EWM-PCA-AHP三种方法结合分区结果表现为中等富水区，而单一主成分分析法表现为弱富水区。以上差异反映了两种方法在衡量富水性强弱上存在不同，主要因为，EWM-PCA-AHP三种方法综合考量了各方法各指标在富水性上的全面表现，而主成分分析法一般只能提取解释80%以上的成分，忽略了部分特殊因子，导致在相同级别下的富水性区间面积较三种方法结合得到的结果更大。