质子交换膜燃料电池冷启动时阴极催化层内多场耦合的介孔尺度模型*
2020-05-12廖梓豪索振邦石伟玉蒋方明
廖梓豪,魏 琳,索振邦,石伟玉,蒋方明
质子交换膜燃料电池冷启动时阴极催化层内多场耦合的介孔尺度模型*
廖梓豪1,2,3,4,魏 琳1,2,3,索振邦5,石伟玉5,蒋方明1,2,3†
(1. 中国科学院广州能源研究所,广州 510640;2. 中国科学院可再生能源重点实验室,广州 510640; 3. 广东省新能源和可再生能源研究开发与应用重点实验室,广州 510640;4. 中国科学院大学,北京 100049; 5. 上海捷氢科技有限公司,上海 201800)
为详细解析质子交换膜燃料电池(PEMFC)零下温度启动过程,建立了电池冷启动时多场耦合过程的介孔尺度数值模型。几何模型基于随机网格法(SGM)重建的催化层介孔结构,数学模型描述了物质传输、电荷传输、电化学反应和汽−冰相变过程。数值分析了电池冷启动过程中催化层内冰的生成和演化,重点探讨了冰的生成及形貌对电池性能的影响,推导出电化学活性反应面积与结冰量的关系式。
燃料电池;数值模拟;介尺度;催化层;冷启动
0 引 言
质子交换膜燃料电池(proton exchange membranefuel cell, PEMFC)具有能量转化效率高、启动快、零排放等优点,应用前景广阔[1]。然而,PEMFC的规模化使用仍然面临诸多挑战。例如,电池自零下温度环境启动时,可能会因结冰导致反应位点被覆盖或者反应(产)物传输通道被堵塞而无法启动。
数值模型是研究PEMFC内多场耦合过程的重要手段和工具。MAO等[2]首先建立了PEMFC的三维冷启动模型,研究了冷启动时电流密度、含水量和冰的三维分布特征;JIANG等[3]为了解PEMFC冷启动时非等温特性,研究了因温度升高导致电−热−气(水)传输物性的改变及其对电池冷启动性能的影响。尽管宏观尺度冷启动模型[3-5]已经实现PEMFC冷启动过程的仿真,但是尚不能够对结冰形貌等进行动态可视化,宏观模型中催化层(catalyst layer, CL)内含冰量对物质输运以及电化学有效反应面积的影响关系式都是基于纯粹的经验关系式,缺乏必要的微观基础。相对于宏观均质模型,介孔模型基于电极的介孔微结构建模[6-7],模型结果可揭示电极的构效关系,可用于设计或优化电极微孔结构,还可获得更准确的有效传输物性等宏观参数(或关系式)[8]。WANG等[9]首次利用理想规则结构的催化层建立了PEMFC过程介孔尺度数值模型,并研究了催化层形貌(孔径、厚度和孔隙率)对电池性能的影响,随后模型进一步发展为基于随机催化层微结构[10]。
微孔结构乃孔尺度模型的基础。微结构重建方法主要分为实验重建法[11]和数值重建法[6,12]。与实验重建法相比,数值重建法具有节省时间和降低成本等优点。随机网格法[13]是数值重建法的一种,作为Monte Carlo模拟在Ising模型的一种扩展,能利用电极的统计学数据对电极结构进行重建,计算速度较快,重建结构能较好地重现原结构的统计特征。
本文基于随机网格法重建催化层介孔结构,针对PEMFC冷启动时催化层内发生的电−热−气(水)传输、电化学反应和结冰的多场耦合过程,建立了介孔尺度模型。研究了冷启动过程中,冰的形成和分布以及冰的形成对传质及电化学反应的影响,详细分析了PEMFC冷启动行为特性。
1 阴极催化层微结构重建
拟重建的催化层厚度为15 μm,由固体混合相(mixed solid, MS)(包括炭黑、Pt和离子聚合物)和孔相(pore, P)组成,各相体积分数见表1。采用随机网格法[14](stochastic grid method, SGM)重构微结构,重建结构的两点自相关函数由实际催化层的SEM图(图1)提取,SEM图的像素位点尺寸为31.716 nm,因此在厚度方向()上设置473个数值单元来代表厚度为15 μm的催化层;在另外两个方向(、)上各设置20个数值单元。重建结构如图2,其中红色代表固体混合相、淡蓝色为孔相。

表1 催化层的各相组成
由随机行走模型[15]计算得到重建结构的扭曲率为1.505,与实际测试结果大致吻合[16]。采用Hoshen-Kopelman聚类分析算法对重构微结构进行连通性分析,连通的孔相和MS相分别占各自总量的97.26%和99.39%。

图1 阴极催化层的SEM图

图 2 重建结果(红色为固体混合相,淡蓝色为孔相)
图3所示为重构微结构的各相体积分数(截面平均)沿电极厚度方向的变化曲线,各相体积分数在平均体积份额附近波动,波动幅度小于10%。图4将重构微结构的孔径分布与压汞实验(mercury injection experiment, MIP)结果进行了对比。实验曲线中的两个峰分别代表燃料电池催化层内的微孔和大孔,重建结构中的孔径分布接近目标电极的大孔区域;本文重建结构的解析度小于实际的微孔尺寸,故重建结构无法呈现微孔。

图3 各相体积分数沿电极厚度方向的变化

图4 重建催化层的孔径分布与实验结果的对比
2 数值模型
2.1 模型假设
阴极催化层位于质子交换膜(proton exchange membrane, PEM)和气体扩散层(gas diffusion layer, GDL)之间(如图5示),= 0处为催化层与气体扩散层交界面,=L(L= 15 μm)处为催化层与PEM交界面;GDL为氧气、水蒸气和电子传输提供通道,PEM为质子和膜态水传输提供输运路径。从GDL侧进入的氧气与阳极反应产生的电子(经外电路后由GDL侧进入)和质子(通过PEM侧进入)在催化层内相遇,在催化剂作用下在活性位点(相界面)发生电化学反应。产物水一部分以水蒸气形式向GDL侧扩散;另一部分以膜态水的形式向PEM侧扩散(回扩散)。此外,电渗作用会使阳极及PEM内部分膜态水迁移到阴极催化层内。当催化层内的水(水蒸气)出现局部过饱和时,将发生相变而形成冰。
模型主要假设如下:①结冰为汽−固凝华过程,且结冰只发生在孔隙之中;②电化学反应发生在孔相和固体混合相之间的交界面;③为专注于研究水的输运对冷启动的影响,模型仅考虑等温冷启动过程[16-17];④忽略催化层内超低速流动对流传质;⑤忽略催化层中微孔对传质与电化学反应的贡献。

图5 阴极催化层模型的电荷及物质输运示意图
2.2 控制方程
模型求解5个控制方程,分别是氧气浓度、水蒸气浓度、膜含水量方程及质子、电子负荷传输方程。
孔相中的氧气和水蒸气传输方程为:





针对离子聚合物内的水传输,膜含水量方程为:
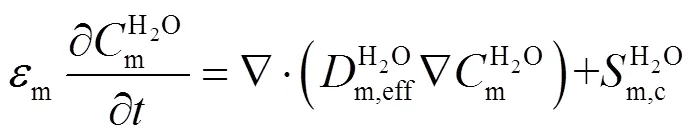

离子聚合物内与孔隙中的水浓度可用Springer关系式[18]描述:
= 0.043 + 17.18− 39.852+ 36.030﹤≤ 1 (7)

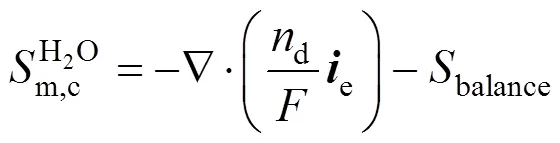
其中:d为电渗系数;e为质子电流;balance为水蒸气和含水量方程在相界面处因热力学平衡过程所导致的源项。




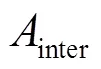

电荷方程分为质子势e方程(13)与电子势s方程(14):

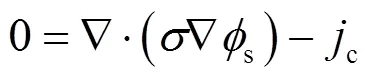

模型的主控方程与源项归纳总结于表2中。
在阴极的电化学反应动力学可用Tafel动力学表示:


模型参数大都来源于MAO等的报道[2],部分参数来源于CRC手册[19]或合作企业提供的实测结果,材料的物性及部分主要的模型参数列于表3。
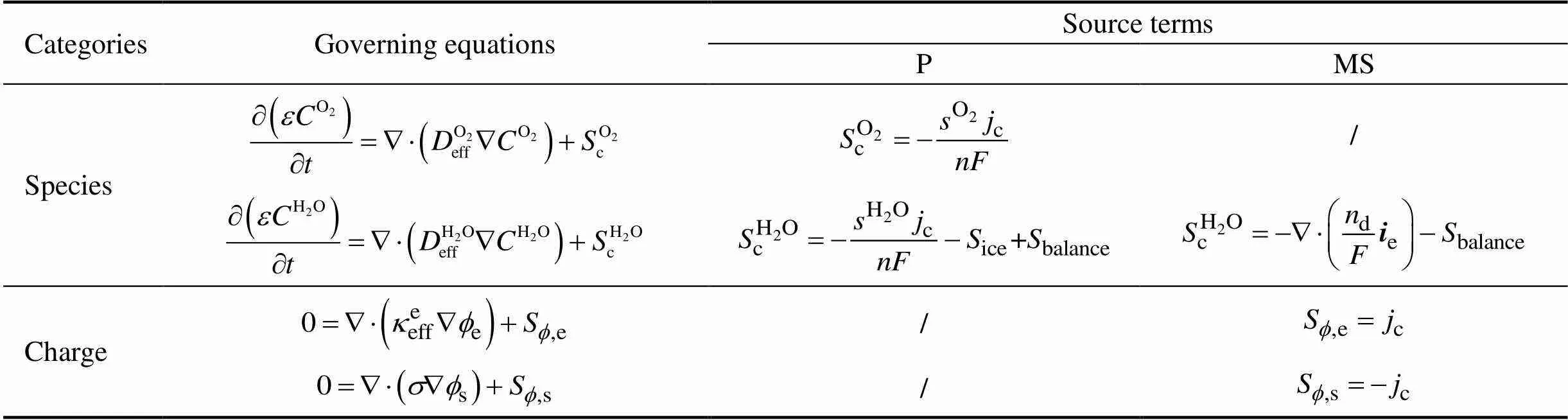
表2 模型主控方程及源项

表3 材料的物性及部分计算参数
Notes: * data from collaborators; **results from the reconstructed structure.
2.3 初边界条件和求解方法
当= 0 s时,电极内氧气浓度为10 mol/m3,孔相及固相中水浓度依据环境条件(0.1 MPa,启动温度)下相对湿度RH = 38%给定。
氧气由气流通道向CL扩散,水蒸气由CL向气流通道扩散;在PEM/CL边界考虑零流条件,则有:


在PEM/CL的边界上,引入净水传输系数[20]来衡量催化层与质子交换膜之间水的传输量;在CL/GDL界面,膜中水含量传输流为0,则有:

其中,/2代表电化学反应产生水的速率。
在= 0和=L处加载电流,=L处的电子电势固定为0 V,故电荷方程的边界条件为:


利用商业计算流体软件Fluent求解,通过用户自定义函数(user-defined functions, UDFs)定义方程的各种源项和物性参数等;基于有限体积法离散求解,瞬态项离散采用完全隐式格式,空间导数项采用中心差分格式差分,采用代数多重网格(algebraic multi-grid, AMG)迭代法加速收敛。模型中数值单元为重建结构(图2)的微元。
3 结果与分析
所求解的算例及其条件如表4所示,电池在恒电流下启动,首先以基础算例分析和讨论模型结果,然后分析讨论变参数(算例1 ~ 算例4)结果。

表4 算例汇总
3.1 结冰形貌(基础算例)
模型能预测PEMFC冷启动过程中冰在催化层内的形貌和分布状态。在5 s时开始在孔隙中有冰生成,图6选择绘制了不同时刻孔隙中含冰量的三维分布。9.5 s时冰在催化层内已经初步形成,随着时间的推移,冰的份额增加、逐渐覆盖催化层内孔隙,而且冰占据的区域向PEM侧扩展。
图7中截面上的含冰量分布显示出了冰在孔隙内的局部非均匀生成状态。较多冰在孔隙中靠近MS相处生成,孔隙中部位置冰的份额明显较少,这与结晶过程中晶体会优先在固体表面形成的成核理论描述一致。

图6 催化层内含冰量分布及其随时间演化

图7 t =18.5 s时催化层中部x截面的含冰量分布
图8显示了不同时刻沿着轴方向的平均含冰量分布,由于重构催化层局部孔隙分布不均匀(图3)及孔隙内冰的不均匀产生(图7),冰在占据孔隙时呈现出不均匀态势,而且不均匀程度随着含冰量的增加愈发明显。另外,从图中可以看出,当含冰量增加时,整体冰含量上升,而冰集中在0.75(=/L,= 1为CL/PEM界面)区域,并在= 0.5附近出现最大值,而在> 0.75区间基本没有冰的生成。冰在催化层内的分布与在= 0和= 1的水传输边界条件及电池的启动参数等有关。

图8 沿x轴方向的含冰量分布及其随时间演化
3.2 结冰对传质和电化学反应的影响(基础算例)
图9a所示为不同时刻催化层内氧气平均浓度沿着轴方向的变化情况。从GDL传输进来的氧气由于反应的消耗而沿方向有明显的下降趋势,在结冰之前(< 5 s),氧气在催化层内部的分布趋于稳定;当冰开始形成时,由于冰会改变催化层形貌且增加传质阻力,随着内部含冰量的增加,氧气浓度沿方向的下降越来越显著。尽管如此,可能是由于局部含冰量不均匀分布(参见图7和图8),氧气在催化层内部的传输通道并没有完全被阻断,在靠近PEM处(= 1)的氧气浓度没有因为大量结冰(= 18.5 s)而下降至零。
图9b所示为离子聚合物内的水含量沿着轴方向的分布。在冷启动初期(0.5 s与3.5 s),水在催化层内积累,整体含水量上升,当局部达到饱和(= 14)时,水平衡作用使得更多的水析出并于孔隙中发生相变,而离子聚合物内的水含量保持在饱和值;随着时间的推移,形成的冰覆盖界面表面并阻碍了离子聚合物内的水向孔隙内传输,导致水含量达饱和值的区域向PEM侧扩展,形成如图6所示冰的生成区域向靠近PEM侧扩展的现象。

为比较不同时刻催化层内电化学反应的强度以及含冰量对反应的影响,图10a显示了6.5 s与18.5 s时的输运电流密度(c)分布。6.5 s与18.5 s时电化学反应均集中在靠近PEM侧(= 1)的区域,而在阴极CL和阴极GDL的交界面处(= 0),c接近于0;与6.5 s相比,18.5 s时含冰量更高,伴随着冰覆盖活性反应面积,电化学反应区域有向= 0端转移的趋势。
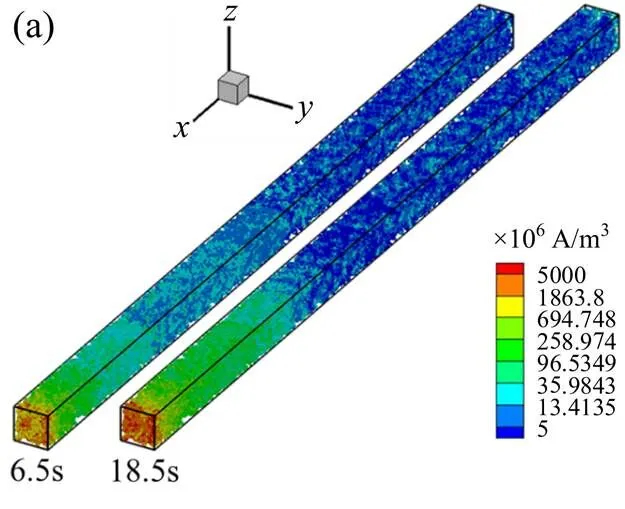
结合图9b与图10a可以看出,水的分布与电化学反应的主要场所不一致。图10b给出了6.5 s与18.5 s时的质子电流密度(e)的分布,质子电流密度在= 1附近较大,并且随着含冰量的增加,质子电流更集中在= 1端附近区域,可以推断阴极催化层内电渗作用对水分布的影响不明显,而图9b显示离子聚合物内在= 1附近水含量较低,图8显示= 1附近区域没有冰生成,可能是由于PEM/CL界面处设置的负的净水传输系数(见表4)导致的。

图11 平均过电势随含冰量的演化

3.3 电化学有效反应面积与结冰量的关系式
当冰在催化层内形成时,部分活性反应面积将会被覆盖,影响电化学反应的进行。为了研究电化学有效反应面积与含冰量的关系,定义电化学有效反应面积比eff为催化层内没有被冰覆盖的活性反应面积与总活性面积的比值:

图12示出了各算例下仿真得到的Seff与总含冰量s的关系,并与宏观冷启动模型中常采取的线性关系式Seff = 1− s对比,图中算例1 ~算例4对应表4中算例。
从图12中可知,仿真结果中的eff均随着含冰量的增加而减少,各eff曲线的重合度很高(不同算例之间的偏差小于10%),但与常用的线性关系式有明显偏离;仿真结果的有效反应面积的减少速率更快,覆盖所有的活性反应面积不需要完全堵塞孔隙。根据仿真结果拟合得到:

式(24)具有一定的介观尺度基础,预期可改进宏观冷启动模型的计算精度。
4 结 论
基于PEMFC催化层重建结构建立了电池冷启动时多场耦合过程的介孔尺度数值模型。模型考虑了冷启动时电池内的反应物/产物和电荷传输、电化学反应过程,能够用以深入研究电池冷启动时阴极催化层内的电−气−汽(水)传输、电化学反应和结冰等。
数值仿真结果揭示了冷启动时冰的生成对催化层内电化学反应、水的生成和传输、氧气的传输等的影响,再现了冷启动过程中电极内生成冰的形貌和分布,分析并推演得到电化学活性面积与冰含量的宏观关系式。该关系式与常用的线性关系式有较大差异,如果用于宏观模型,预期可以提高模型计算精度。
符号表:
水活度
面积,m2
Bruggeman指数
摩尔浓度,mol/m3
扩散系数,m2/s
EW 离子聚合物的当量质量,kg/mol
法拉第常数,96 485 C/mol
电流负载,A/m2
0交换电流密度,A/m2
e质子电流密度,A/m2
输运电流密度,A/m3
摩尔质量,kg/mol
反应电子迁移数
d电渗系数
速率,s−1
通用气体常数,8.314 J/(mol·K)
源项,反应面积比
整体含冰量
温度,K
0阴极电化学反应热力学平衡电势,V
传输系数,净水传输系数
体积分数
过电势,V
离子传导率,S/m
离子聚合物内含水量
密度,kg/m3
电势,V
电子传导率,S/m
角标:
a 环境
c 阴极
e 电解质
eff 有效的
freeze 结冰
g 气体
组分
inter 界面
ice 冰
L 总长度
m 模型,离子聚合物
r 反应
ref 参考值
s 固体
sat 饱和值
[1] WEE J H. Applications of proton exchange membrane fuel cell systems[J]. Renewable and sustainable energy reviews,2007, 11(8): 1720-1738. DOI: 10.1016/j.rser.2006.01.005.
[2] MAO L, WANG C Y, TABUCHI Y. A multiphase model for cold start of polymer electrolyte fuel cells[J]. Journal of the electrochemical society, 2007, 154(3): B341-B351. DOI: 10.1149/1.2430651.
[3] JIANG F M, FANG W F, WANG C Y. Non-isothermal cold start of polymer electrolyte fuel cells[J]. Electrochimica acta, 2007, 53(2): 610-621. DOI: 10.1016/j.electacta.2007.07.032.
[4] JIAO K, LI X G. Cold start analysis of polymer electrolyte membrane fuel cells[J]. International journal of hydrogen energy, 2010, 35(10): 5077-5094. DOI: 10.1016/j.ijhydene.2009.09.004.
[5] YAO L, PENG J, ZHANG J B, et al. Numerical investigation of cold-start behavior of polymer electrolyte fuel cells in the presence of super-cooled water[J]. International journal of hydrogen energy, 2018, 43(32): 15505-15520. DOI: 10.1016/j.ijhydene.2018.06.112.
[6] KIM S H, PITSCH H. Reconstruction and effective transport properties of the catalyst layer in PEM fuel cells[J]. Journal of the electrochemical society, 2009, 156(6): B673-B681. DOI: 10.1149/1.3106136.
[7] LANGE K J, SUI P C, DJILALI N. Pore scale modeling of a proton exchange membrane fuel cell catalyst layer: effects of water vapor and temperature[J]. Journal of powersources, 2011, 196(6): 3195-3203. DOI: 10.1016/j.jpowsour.2010.11.118.
[8] WU W, JIANG F M. Microstructure reconstruction and characterization of PEMFC electrodes[J]. International journal of hydrogen energy, 2014, 39(28): 15894-15906. DOI: 10.1016/j.ijhydene.2014.03.074.
[9] WANG G Q, MUKHERJEE P P, WANG C Y. Direct Numerical Simulation (DNS) modeling of PEFC electrodes:part I. Regular microstructure[J]. Electrochimica acta, 2006,51(15): 3139-3150. DOI: 10.1016/j.electacta.2005.09.002.
[10] WANG G Q, MUKHERJEE P P, WANG C Y. Direct Numerical Simulation (DNS) modeling of PEFC electrodes: part II. Random microstructure[J]. Electrochimica acta, 2006, 51(15): 3151-3160. DOI: 10.1016/j.electacta.2005.09.003.
[11] SHEARING P R, BRADLEY R S, GELB J, et al. Using synchrotron X-ray nano-CT to characterize SOFC electrode microstructures in three-dimensions at operating temperature[J]. Electrochemical and solid-state letters, 2011, 14(10): B117-B120. DOI: 10.1149/1.3615824.
[12] SIDDIQUE N A, LIU F Q. Process based reconstruction and simulation of a three-dimensional fuel cell catalyst layer[J]. Electrochimica acta, 2010, 55(19): 5357-5366. DOI: 10.1016/j.electacta.2010.04.059.
[13] 吴伟, 蒋方明, 曾建邦. LiCoO2电池正极微结构重构及有效传输系数预测[J]. 物理化学学报, 2013, 29(11): 2361-2370. DOI: 10.3866/PKU.WHXB201309032.
[14] PROMENTILLA M A B, SUGIYAMA T, HITOMI T, et al. Quantification of tortuosity in hardened cement pastes using synchrotron-based X-ray computed micro- tomography[J]. Cement and concrete research, 2009, 39(6): 548-557. DOI: 10.1016/j.cemconres.2009.03.005.
[15] PATEL K K, PAULSEN J M, DESILVESTRO J. Numerical simulation of porous networks in relation to battery electrodes and separators[J]. Journal of power sources, 2003, 122(2): 144-152. DOI: 10.1016/S0378-7753(03)00399-9.
[16] GE S H, WANG C Y. In situ imaging of liquid water and ice formation in an operating PEFC during cold start[J]. Electrochemical and solid-state letters, 2006, 9(11): A499-A503. DOI: 10.1149/1.2337860.
[17] TAJIRI K, TABUCHI Y, WANG C Y. Isothermal cold start of polymer electrolyte fuel cells[J]. Journal of the electrochemical society, 2007, 154(2): B147-B152. DOI: 10.1149/1.2402124.
[18] SPRINGER T E, ZAWODZINSKI T A, GOTTESFELD S. Polymer electrolyte fuel cell model[J]. Journal of the electrochemical society, 1991, 138(8): 2334-2342. DOI: 10.1149/1.2085971.
[19] HAYNES W M. CRC handbook of chemistry and physics[M]. Raton: CRC Press, 2015.
[20] ZAWODZINSKI T A, DAVEY J, VALERIO J, et al. The water content dependence of electro-osmotic drag in proton-conducting polymer electrolytes[J]. Electrochimica acta, 1995, 40(3): 297-302. DOI: 10.1016/0013-4686(94)00277-8.
[21] WANG C Y. Fundamental models for fuel cell engineering[J]. Chemical reviews, 2004, 104(10): 4727-4766. DOI: 10.1021/cr020718s.
A Mesoscopic Pore-Scale Model of Multi-Disciplinary Coupling in PEMFC Cathode Catalyst Layer during Cold Start
LIAO Zi-hao1,2,3,4, WEI Lin1,2,3, SUO Zhen-bang5, SHI Wei-yu5, JIANG Fang-ming1,2,3
(1. Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China; 2. CAS Key Laboratory of Renewable Energy, Guangzhou 510640, China; 3. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development, Guangzhou 510640, China; 4. University of Chinese Academy of Sciences, Beijing 100049, China; 5. Shanghai Hydrogen Propulsion Technology Co., Ltd., Shanghai 201800, China)
In order to have a deep understanding of the cold start of proton exchange membrane fuel cell (PEMFC) from sub-zero temperature, a mesoscopic pore-scale model of multi-disciplinary coupling in cathode catalyst layer (CL) was established. The geometry model is a 3-dimensional pore-structure of CL reconstructed by the random grid method (SGM), and the species transport, charge transport, electrochemical reactions and phase change of water were described by mathematical model. The formation and evolution of ice in CL during cold start were simulated and analyzed, the effects of ice formation and morphology on battery performance were discussed, and a correlation of the electrochemical active reaction area (ECA) to the amount of ice formation in CL was derived from the simulation results.
fuel cells; numerical simulation; mesoscale; catalyst layer; cold start
TK91;TM911.48
A
10.3969/j.issn.2095-560X.2020.02.001
2095-560X(2020)02-0081-10
2019-11-11
2019-12-26
上海汽车工业科技发展基金会项目(1706);广东省科技发展专项资金(前沿与关键技术创新方向—重大科技专项)项目(2017B01012003);广东省自然科学基金项目(2016A030313172);广东省自然科学基金−重大基础研究培育项目(2015A030308019)
蒋方明,E-mail:jiangfm@ms.giec.ac.cn
廖梓豪(1994-),男,博士研究生,主要从事质子交换膜燃料电池数值模拟及相关实验研究。
蒋方明(1973-),男,博士,研究员,博士生导师,2001年博士毕业后曾先后就职于德国的IMM公司、葡萄牙的阿维诺大学、美国的宾州州立大学,2010年底开始回国工作。主要从事绿色能源/动力相关热物理工程的前沿科学技术问题的研究。
猜你喜欢
——“有序介孔高分子和碳材料的创制和应用”获2020年度国家自然科学奖一等奖
