无线传感器网络数据的个性化加权在线集成学习算法

刘 伟,王 琦,于化龙

(江苏科技大学 计算机学院,江苏 镇江 212003)

E-mail:weiliu@stu.just.edu.cn

1 相关工作

近年来,无线传感器网络已广泛应用于生产生活的各个领域,在环境监测[1]、现代农业[2]、自然灾害预警[3]等领域发挥着重要的作用.为了获取全面、准确的信息,通常在监控区域内部署大量传感器节点.为了完成数据采集任务,通常采用基于分簇的无线传感器网络路由协议[4-7],即把网络在逻辑上划分为若干簇,每个簇由一个簇首和若干个簇内成员节点构成.簇内成员节点负责采集感知数据并发送给簇首,簇首负责簇内通信调度、数据融合以及发送数据至基站,基站以互联网的方式最终将数据发送给用户.

无线传感器网络作为一种数据采集型网络,其数据是以数据流的形式传递给用户[8,9],该数据流具有时间顺序性、分布变化快速、潜在无限、数据间关联性强等特点[10].针对无线传感器网络的数据特点,如何准确地对传感器数据进行精确的在线预测,便成为一个急需解决的问题.

传统的基于机器学习方法的预测模型归根结底是对某一静态数据分布的学习,即通过先验数据训练出一个误差最小的预测模型,无需考虑因为数据的变化而更新模型的问题.但是,在无线传感器数据流环境中,一些数据分布是随着环境变化和时间推移而发生改变,且这种改变是不可预测的,即产生概念漂移现象[11],如在一个测量温度的传感器网络中,某年可能出现极寒或极热情况,则该年的数据分布将不同于历史数据.如果还是依靠旧数据训练的模型用于对新数据进行预测,则表现出较差的泛化性能.因此,在设计无线传感器网络数据的预测模型时,需要考虑因数据变化而带来的概念漂移问题.

针对无线传感器网络数据流的特点,文献[10]介绍了包括决策树、分类关联规则等集成分类模型.文献[12]提出了自适应集成方法,对概念漂移的数据流进行分类.文献[13]给出了一种基于数据块的在线处理概念漂移数据流的集成分类方法.文献[14]则采用了在线权重集成方法和在线随机森林方法,来设计集成分类方法.众多学者已将集成学习应用于处理概念漂移数据流,即把多个不同的弱预测模型组合成一个强预测模型[15],利用不同预测模型之间的差异,来提高模型的泛化性能.集成学习预测模型具有更高的预测准确度,可以很好地适应概念的变化,将概念漂移的影响削弱在共同决策中.集成学习预测模型有两个主要的问题需要解决,一是如何得到若干个弱预测模型,二是如何选择一种组合策略,将这些弱预测模型组合成一个强预测模型.

在本文,我们提出并分析了一种新颖的个性化加权在线集成算法.使用先验数据对模型进行训练学习,采用加权投票的组合策略,将多个弱预测模型组合成一个强预测模型.为了适应概念漂移现象,按照顺序一批接一批地处理实例,每次处理一批实例后更新集成学习预测模型.我们的贡献如下:

1)基于无线传感器网络数据流的时间顺序性,将先验数据划分为若干数据块,训练出若干弱预测模型.

2)考虑前后数据块概率分布的差异性,通过计算各数据块之间的K-L散度值,确定各弱预测模型的权重,进行动态加权集成.

2 所提方法

为了对无线传感器网络的数据流进行预测,本文提出了个性化的加权在线集成学习模型.如图1所示,对于无线传感数据流,该方法首先按照时间顺序将先验数据划分为若干数据块,对于最新接收到的数据块Bm,保留距离新数据块最近的n个数据块Bm-n,…,Bm-1,并通过这n个数据块,分别训练出n个预测模型,同时假设每个数据块均符合多维高斯分布,并分别计算及记录每数据块的均值和方差.通过分别计算新数据块到最近的n个数据块之间的K-L散度值,确定其相似度,进而据此计算每个模型对应的投票权重,最终生成一个加权集成预测模型.每次处理一批实例后,采用新模型替换集成学习预测模型集中距离新数据块最远的一个预测模型.

图1 个性化集成在线学习预测模型示意图

2.1 K-L散度计算

高斯分布是自然科学和行为科学中最常见的一种概率分布形式.因此,可以近似地认为无线传感器网络中各数据块在每一特征维度上均服从高斯分布[16,17].

对于单变量高斯分布,其概率密度函数可表示如下:

(1)

其中,μ为数学期望值,σ为方差.

对于多变量高斯分布,其概率密度函数则可表示如下:

(2)

其中,μ为期望值,Σ为协方差矩阵.

K-L散度,是一种度量两种概率分布P1和P2之间差异的度量测度.假设概率分布P1表示真实分布,概率分布P2表示拟合的真实分布,那么则可以通过计算它们之间的K-L散度值来度量使用概率分布P2拟合真实分布P1所产生的信息损耗[18].多变量高斯分布的K-L散度值可以按照公式(3)来进行计算得到:

DKL(P1‖P2)

=EP1(logP1-logP2)

(3)

其中,Σ1和Σ2分别代表两个数据集的协方差矩阵,而μ1和μ2则表示它们的期望值.显然,当两个分布完全相同时,则它们的K-L散度值为零.当两个分布的差别较大时,则它们的K-L散度值也会较大,且会随着分布差异的增大,K-L散度值越变越大.

2.2 基于K-L散度的权重分配策略

由于无线数据传感器网络数据流具有时间顺序性这一特点,因此可以按照时间分布规律将数据划分为若干个数据块.如图1所示,假设在集成预测模型中,我们只保留与最新接收的数据块Bm最邻近的n个数据块Bm-n,…,Bm-1以及预测模型Cm-n,…,Cm-1,并计算各个数据块的期望值μm-n,…,μm-1与协方差矩阵Σm-n,…,Σm-1,同时计算Bm的期望值μm和协方差矩阵Σm.

按照公式(3),分别计算Bm到Bm-n,…,Bm-1之间的K-L散度值Dm-nm,…,Dm-1m.假设Dim最小,则表明第i块数据与第m块数据的概率分布最为相似,则显然采用对应的预测模型Ci对新数据块Bm进行预测也要最为准确,故理应为其分配最大的权重.本文引入公式(4)所示的衰减函数,来计算得到权重所有的wm-nm,…,wm-1m.

w=e-kx

(4)

其中,k为一个常数,用于调控权重的衰减速度,x表示对应的K-L散度值,w则为计算得到的权重值.显然,利用该式,可以建立K-L散度值与权重之间的负相关关系,即K-L散度值越大,二者差异也越大,对应的投票权重也越小.

计算Bm被n个预测模型预测的结果Rn,Rn-1,…,R1,将具有相同结果的预测模型聚类,假设有s类,并对每类的w进行求和得{W1,W2,…,Ws},取其中最大值所对应的类别作为最终的预测结果.

2.3 在线加权集成预测模型

本文所提出的个性化加权在线集成算法,其详细的算法流程如表1所示.

表1 算法流程

Table 1 Flowchart of the proposed algorithm

3 实验与结果

3.1 度量标准

本文主要采用预测精度作为衡量算法性能优劣的度量指标[19],对于精度,其计算公式如下:

(5)

其中,total_num为新数据块中的样本总数,correct_num为预测正确的样本数,Accuracy值越大,则表明预测精度越高.

3.2 数据集描述

本文采用Sensor Stream数据集(1)http://www.cse.fau.edu/～xqzhu/stream.html.对所提算法的性能进行测试,下面将对该数据集进行简单介绍.

Sensor Stream数据集来源于英特尔-伯克利实验室.无线传感器网络由54个传感器节点组成,每隔1～3分钟采集网络内各个传感器节点的温度值、湿度值、光线亮度值和自身电压值等,共计执行2个月的数据采集任务.该数据集使用传感器节点ID作为类标,令温度值、湿度值、光线亮度值和自身电压值作为特征值.因此,对于该数据集,学习任务就是要完全根据传感器数据和相应的记录时间来正确预测传感器的ID(54个传感器中的1个).

由于该数据集中的样本数量过多且相互独立,为了简化实验的过程,本文截取了原始数据集中传感器节点ID为1,2,3,4的所有样本,并通过异常值处理、冗余数据处理后得到简化后数据集.继而,按照时间顺序将简化后的数据集划分为若干数据块B1,B2,…,Bn,平均每个数据块中包含3500个样本,本文选择前50个数据块来运行实验并验证所提算法的性能.

3.3 实验设置

为了表明本文算法与具体采用何种分类器是无关的,本文分别采用了决策树、K近邻和支持向量机等三种不同的分类算法对其进行验证.

决策树采用的是CART算法;K近邻算法中的参数K预设为7;支持向量机选择高斯核函数,惩罚因子统一设置为1,核函数系数则设置为样本特征数的倒数.

3.4 实验和结果

本文共设计了两组实验,第一组用来确定本文算法的最佳参数设置,第二组实验则用来验证本文算法的优越性.为了证明本文算法的优越性,也将其与基线的算法进行了对比,即不考虑分布差异的无加权集成预测模型.

3.4.1 网格搜索方法确定最优参数

如图2所示,当将衰减常数k固定为5时,通过调控集成规模n的值可以观察到这一参数对算法总体性能的影响规律.从该图中可以看出,若集成规模n=5,无论决策树、K近邻,还是支持向量机分类器均可以得到最高的分类精度.

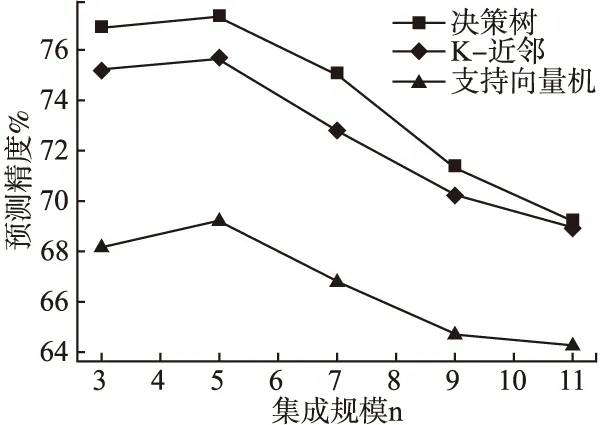
图2 n值变化对算法性能的影响

如图3所示,当将集成规模n固定为5时,我们也可以通过调控公式(4)中的衰减常数k的值来观察其影响规律.从该图中可以观察到:若k=10时,基于决策树、K近邻、支持向量机算法的分类器分别对49个数据块进行预测,且平均预测准确率最高.

图3 k值变化对算法性能的影响

3.4.2 算法比较与结果分析

当n=5,k=10,即保留距离本次数据块最近的5个数据块和其所对应的分类器,并分别计算本次数据块与前5个数据块之间的K-L散度值,并根据衰减常数k值,确定投票权重值.根据投票机制,确定投票值最大的类别,作为该数据块中某个样本的分类值.

如图4所示,以决策树为集成中的个体分类模型,本文所提出的基于K-L散度加权的集成预测模型在49个数据块上的平均预测精度为78.9%,相比于无加权集成预测模型提高了近5.7%.其中,在31个数据块上的预测精度均优于无加权集成预测模型,在10个数据块上的预测精度达到了100%.

如图5所示,以K近邻为集成中的个体分类模型,本文所提出的基于K-L散度加权的集成预测模型在49个数据块上的平均预测精度达到了78.3%,相比于无加权的集成学习预测模型提高了近5.6%.其中,在30个数据块上的预测精度均优于无加权集成预测模型,在10个数据块上的预测精度达到了100%.

如图6所示,以支持向量机为集成中的个体分类模型,本文所提出的基于K-L散度加权的集成预测模型在49个数据块上的平均预测精度达到了71.3%,相比于无加权的集成学习预测模型提高了近4.3%.其中,在32个数据块上的预测精度均优于无加权集成预测模型,但仅在1个数据块上的预测精度达到了100%.

图4 基于决策树的集成学习预测模型的预测准确度

图5 基于K-近邻的集成学习预测模型的预测准确度

图6 基于支持向量机的集成学习预测模型的预测准确度

通过上述的实验结果可以看出:本文算法无论采用何种基分类器,其性能均要优于无加权的集成预测模型.一方面证明了本文算法并不依赖于某种具体的基分类算法,另一方面也证明了考虑分布差异,进而进行个性化加权的必要性.至于在三种不同分类器上,最终的分类精度有很大不同,则完全是由基分类器自身特性及参数设置而导致的,并不影响验证本文算法的优越性.

4 结 语

针对无线传感器网络数据流易于产生分布漂移这一特点,本文设计了一种个性化的加权在线集成分类算法.该算法充分考虑了分布间的差异性,并通过K-L散度对其进行量化,可以有效评估已建立的各个分类器对新数据块准确预测的贡献程度,并将其转化为集成投票权重,有效地提升了对传感器数据流的预测精度.特别地,在集成预测模型中,本文采用了动态的基分类器更新策略,可以有效地降低决策的时间复杂度,能够满足无线传感数据实时性的需求.通过大量实验验证了本文算法的有效性、可行性及优越性.