基于重构邻域策略的分解多目标进化算法
2020-05-12郭海东王丽萍徐梦娜
曹 鸽,郭海东,王丽萍,徐梦娜
1(浙江工业大学 经贸管理学院,杭州 310023)
2(浙江工业大学 信息智能与决策优化研究所,杭州 310023)
3(浙江工业大学 计算机科学与技术学院,杭州 310023)
E-mail:gimmg@zjut.edu.cn
1 引 言
多目标优化问题各个目标之间相互冲突,通常情况下,无法使各个目标同时达到最优[1],只能获得一组近似Pareto最优解.在生物工程[2,3],经济学[4],工程学[5]等领域存在大量的多目标问题,因此研究并解决多目标优化问题具有十分重要的现实意义.
近几十年以来,大量的多目标进化算法(Multi-Objective Evolutionary Algorithms,MOEAs)被相继提出,MOEAs可以分成三类:
1)基于支配的方法,例如Deb[6]等提出基于Pareto支配关系的快速非支配排序算法(Fast and Elitist Multiobjective Genetic Algorithm,NSGA-II),Zitzler[7]等提出强化Pareto算法(Improving the Performance of the Strength Pareto Evolutionary Algorithm,SPEA2),但该类算法会随目标维度上升非支配解的数量呈指数增长,导致基于Pareto关系对优秀解的选择压力严重衰减,算法容易陷入局部最优;
2)基于指标的方法,Zitzler[8]提出基于超体积的多目标进化算法SMS-EMOA(Improving hypervolume-based multiobjective evolutionary algorithms by using objective reduction methods),但是HV指标的计算代价会随目标维度增加呈指数增长;且在目标维度高于5维的情况下很难实现实际应用;
3)基于分解的方法,Zhang[9]等提出了一种基于分解的多目标进化算法(MOEA/D),将复杂的MOP(Multi-objective Optimization Problem)分解成多个简单的优化子问题,再同时对这些子问题进行求解.这些子问题之间的邻域关系是基于聚合函数来定义的,每个子问题通过来自其相邻子问题的信息进行优化.
邻域结构在MOEA/D中起到重要的作用,原始MOEA/D和其大部分的变体算法,在算法迭代初始,将所有子问题邻域大小都设置成固定数值,这使得每代中所有子问题分配到相同计算资源.然而由于子问题计算复杂度均不相同,对所有子问题都设置同样大小的邻域资源进行优化时,会造成边界子问题搜索资源浪费的问题,而较密集的子问题将面临搜索资源不足的困境.针对以上问题,有学者提出了以下改进算法.Zhao[10]提出了一种自适应改变邻域大小的方式来改善固定邻域存在的缺陷.Zhang[11]提出动态资源分配策略,有效改善了解集的分布性.Qi[12]提出自适应权重调整策略,Wang[13]提出基于全局替换策略的多目标进化算法(MOEA/D Based on Global Replacement,MOEA/D-GR). Jiang[14]提出了一个小生境引导下的交配选择范围设定方案,在优化的MOP的POF(Pareto-optimal front)不连续时仍能有效保持种群多样性.Chiang[15]提出了基于MOEA/D-DE[16]的自适应父代选择机制,根据决策空间上个体之间的欧几里德距离来选择父代解进行基因重组,而不是目标空间中子问题的权重向量之间的距离.选择决策空间中距离最近的T个个体作为交配池,并每隔一定代数自适应调整交配池.Zhang[17]在算法运行每一代中都应用自组织映射来确定种群在决策空间中的分布结构,并为每个解构建交配池,仅允许相同交配池内的解进行基因重组操作.此外,根据过去一定代数内产生新解的表现自适应调整邻域大小.
初始MOEA/D和大部分变体算法基因重组操作父代的选择仅仅基于邻域关系,这种方式不利于算法的优化.因此,适当的调整选择父代的方式,可以大大提升算法性能.本文提出一种重构邻域策略,从邻域和精英解集合中选择父代来进行交叉变异操作产生新解,其中,精英解集合分两步筛选确定,利用垂直距离更新策略筛选出预备精英解集,再通过计算每个预备精英的“潜力值”,并根据“潜力值”排名来筛选精英解集.这种方式突破了以往的MOEA/D选择父代来进行基因重组模式,在不改变邻域规模的前提下(通过邻域关系确定的邻域和精英解集组成的新邻域规模保持一定),本文提出的重构邻域策略在一定程度上可以避免父代中的精英解在迭代过程中丢失,从而有效改善了新一代解的质量,提升了算法收敛速度.
2 研究背景及MOEA/D-DU缺陷分析
2.1 多目标优化问题
多目标优化问题在数学上的定义如下:
Minimize F(x)=(f1(x),f2(x),f3(x),…,fm(x))T
Subjecttox∈Ω
(1)
其中,x=(x1,x2,…,xn)T是决策变量向量,Ω是决策空间内的可行区域,F:Ω→Rm,包含m个目标fi(x)(i=1,2,3,…,m).
2.2 MOEA/D-DU
在MOEA/D-DU(Balancing convergence and diversity in decomposition-based many-objective optimizers)[18]中,采用改进版本的切比雪夫聚合法将问题(1)分解成若干个子问题:
(2)
其中:
ⅰ.Z*为参考点,通常算法使用搜索过程中Fj的最小值来表示;
ⅱ.λ=(λ1,λ2,…,λN)T为在空间中生成均匀分布的权重向量,λj,p≥0,p∈({1,2,…,m}).
初始化种群x1,x2,…,xN(xi∈Ω),其中xi为第i个子问题的当前解.
在MOEA/D-DU中,计算任意两个权重向量之间的欧几里德距离,然后选择距离每个权重向量最近的T个权重向量,对于每一个权重向量λi(i∈[1,N]),其邻域设为B(i)={i1,…,iT}.每个子问题互相独立的依靠于邻域信息进行优化,在邻域中选择父代解并进行基因重组操作产生新解,以此来保持解集的多样性.
2.3 MOEA/D-DU缺陷分析
在MOEA/D更新策略中,交叉变异产生的新解可以替换邻域内的解,不限制替换解个数,这在一定程度上加快种群收敛速度,但是一个新解替换邻域内多个解的更新替换方式可能会导致算法陷入局部最优,同时降低解集多样性.
MOEA/D-DU算法提出垂直距离更新策略,每一代通过计算新解到每个权重向量λj(j=1,2,…,N)的垂直距离,dj,2(y)(j=1,2,…,N),然后从这N个距离中选择K个最小的距离,然后将这K个距离以递增的顺序排序,假设顺序为:dj1,2(y),dj2,2(y),…,djK,2(y),解y逐个与解xj1,xj2,…,xjk进行比较,直到解xjk(k∈{1,2,…,K})的聚合函数值比解y的大,则解xjk被解y替代,并且更新过程终止.由于在当前种群中新解只替换一个解,这在一定程度上提高了解集的质量,保持了解集的多样性,但是大大降低了种群收敛到Pareto前沿面的速度,相比于新解替换多解的算法,算法的收敛速度较为缓慢.
以测试函数DTLZ3为例,从图1可以看出,在二维目标优化问题上,在350代之前,MOEA/D-DU的GD指标值随代数变化曲线在MOEA/D的上方,说明MOEA/D-DU在算法收敛前期的收敛速度与MEOA/D相比较缓慢,在450代之后,MOEA/D-DU的GD值随代数变化曲线在MOEA/D的下方,并逐渐趋于稳定,即MOEA/D-DU的GD值更优,说明MOEA/D-DU求得的近似Pareto前沿能较好地逼近真实的Pareto前沿面,但是从曲线总体走向而言,算法收敛到Pareto前沿面的速度相比MOEA/D较为缓慢.
综上所述,MOEA/D-DU提高了解集的多样性,但是在一定程度上牺牲了种群收敛到近似Pareto前沿面的速度,因此,本文提出重构邻域策略,在一定程度上提高算法的收敛速度,同时通过改变解集的邻域结构平衡算法的多样性和收敛性.
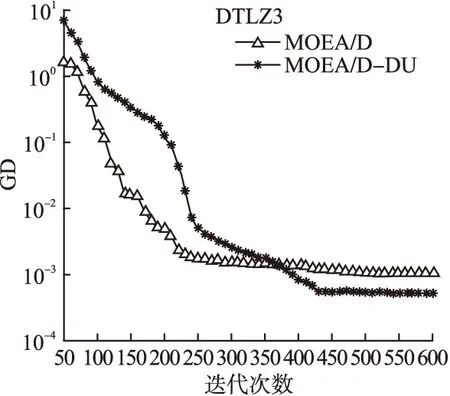
图1 测试函数DTLZ3在3维目标问题上收敛性对比
3 基于重构邻域策略的多目标进化算法(MOEA/D-RNS)
本文提出一种重构邻域策略算法MOEA/D-RNS,算法从子问题邻域和精英解组成的新邻域集合中选择父代进行交叉变异产生新解.其中,精英解分两步筛选确定,利用更新策略筛选出预备精英解集,再通过计算每个预备精英的“潜力值”,并根据“潜力值”排序来选择精英解.
3.1 潜力值定义
潜力值定义:比较解j与邻域内每个解的聚合函数值,将解j优于或等于该邻域解的数量定义为解j在其邻域内的潜力值.
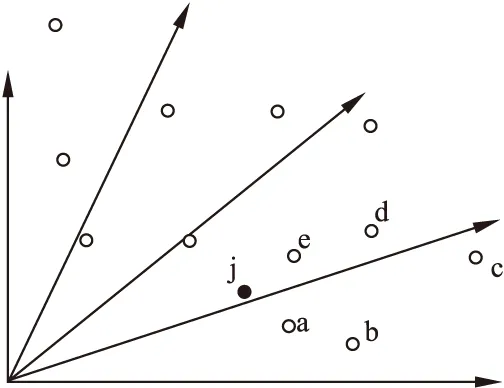
图2 潜力值定义
如图2所示,j的邻域为a、b、c、d、e,比较j与a、b、c、d、e的聚合函数值,图中j的聚合函数值均优于邻域内的a、b、c、d、e这5个解,故j的潜力值为5.潜力值可以反映在某个特定子问题上解质量的好坏.
3.2 算法介绍
算法1为MOEA/D-RNS的整体框架,算法2和算法3分别为预备精英的潜力值计算和重构邻域策略.
算法1为MOEA/D-RNS算法整体框架,加入了重构邻域策略(RNS),预备精英初始化设置为全体个体,设置精英的评判下限T_num,潜力值大于T_num的预备精英被判定为精英.步骤2为计算每个预备精英潜力值num,具体步骤见算法2.
算法1.MOEA/D-RNS算法
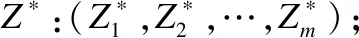
输出:B(i){i1,i2,…,iT1}
1.Fori=1 toN
2.通过算法2计算预备精英的潜力值
3.QL(1)≥QL(2)≥…≥QL(T2) //对每个预备精英根据潜力值的大小进行非减排序,并选取前T2个
4.Best←{best1,best2,…,bestT2} //将步骤2选出的T2个个体(best1,best2,…,bestT2)视为精英点
5.重构邻域策略(算法3)
6.Mating Selection
7.y←GeneticOperators(xi;xk)
8.UpdateIdealPoint(y;z*)
9.(P1)←UpdatePopulation(y;z*;Λ;P;K)
10.a1//找到新解可替换的第一个解a1
11.nn=nn∪P1(1:a1) ∥更新预备精英
12.End for
从预备精英中选择精英:每代迭代开始,对上一代选出的所有预备精英解进行如下操作:计算并比较预备精英解j与其邻域B(j)解的聚合函数值,将预备精英优于邻域解的数量定义为潜力值QL,具体过程见算法2.再将潜力值按照非升序排名,取潜力值排名前T2个预备精英为精英,将这T2个精英作为精英集sindex.
步骤3-步骤4:对所有预备精英按照潜力值大小进行非减排序,选取前T2个预备精英作为精英,在此之后清空预备精英集,以便后续预备精英选取操作.步骤5为重构邻域策略,具体操作见算法3.步骤5为算法3重构邻域策略下的父代选择操作.
步骤9-步骤11为选择预备精英的操作,其中步骤9为MOEA/D-DU的更新过程,选择预备精英:在每代的算法迭代过程中,为下一代算法迭代挑选预备精英,对每个个体i均做如下操作:将离新解y最近的K个邻域解(更新策略选出的离新解最近的K个权重向量对应的K个邻域解),保存在集合P1中,计算新解y和这K个邻域解的聚合函数值.考虑到不可被新解替换的解可能是邻域内较好的解,在一定程度上认为这样的解可以为算法带来性能上的提升,所以将不可替换的解也设置成预备精英,首先找到新解可替换的第一个解a1,将1,…,a1对应的个体视为预备精英,并被纳入集合nn,即nn=nn∪P1(1:a1),∪表示集合合并操作,预备精英保存在nn中.
算法2.计算预备精英的潜力值
初始化:潜力值QL
1.L=length(nn)
∥L为预备精英的数量
2.Fork=1 to length(nn)
3.P2=B(nn(k),:)
∥P2为当前预备精英的邻域
4.Form=1 toT
5.IfF(nn(k))>=F(P2(m))∥预备精英和邻域解聚合函数值比较
6.QL=QL+1 ∥若预备精英k的聚合函数值优于其邻域解m,则潜力值加1
7.End
8.End for
9.num(nn(k))=QL
∥更新潜力值num
10.End for
算法3重构邻域策略,算法迭代过程中,每个子问题i将D(i)={i1,…,iT1}(邻域B(i)中取前T1个个体组成的集合)和精英集sindex(T2个精英构成)组成的集合作为重构后的邻域,这里用D(i)和sindex组成的集合替换邻域B(i).T1和T2满足:T=T1+T2,保证算法的邻域大小与其他对比算法相同.
算法3.重构邻域策略
1.Fori=1 toN
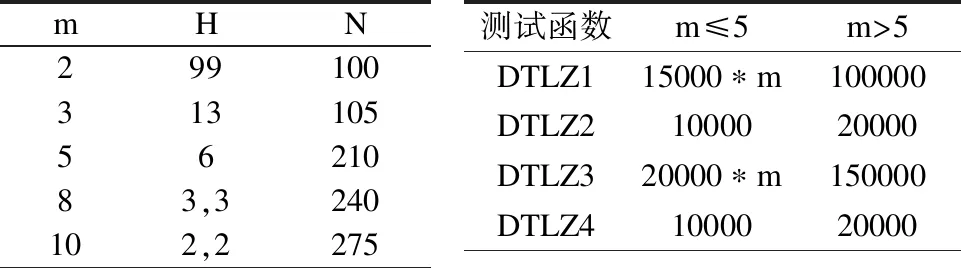
2. If Rand 3.BB=[B(i,1:T1) sindex(1:T2)] 4.P=BB(Rand(Size(B,2))) 5. Else 6.EE=[E(i,1:N-T2)sindex(1:T2)] 7.P=EE(Rand(Size(E,2)) 8.End 9.IfP(1)==P(2) 10.P(2)=P(3); 11.End 为了验证本文所提出的算法性能,我们对ZDT1-4系列测试函数和DTLZ1-4系列测试函数进行测试,分析改进算法MOEA/D-RNS与对比算法MOEA/D[9]、MOEA/D-DE[16]、MOEA/D-DU[18]和NSGA-Ⅲ[19]在IGD和GD指标上的性能表现,测试均在PlatEMO平台[20]上进行,对每个测试函数独立运行30次取平均值和标准差. 根据决策变量的公式n=m+k-1,测试函数DTLZ1对应的k设置为5,DTLZ2-4对应的k设置为10,ZDT1-4系列测试函数的决策变量设置为30.此外,所有算法的其它参数均保持一致.采用模拟二进制交叉和多项式变异,交叉概率Pc=1.0,变异概率Pm=1/n,交叉分布指数(ηc)=20,变异分布指数(ηm)=20.本文中设置,0≤T1,T2≤T/2,所有的对比算法T均设置为20.随着目标维度增加,逼近Pareto前沿面所需的解数量会呈现指数上升,所以需要相应的调整种群规模大小,对比算法的种群规模N设定如表1所示.ZDT1-4系列测试函数评价次数设定为30000,DTLZ1-4系列测试函数在不同维度(m)上的评价次数设定如表2所示. 仿真实验中,为了衡量算法性能,使用如下指标: 1) 反向世代距离(IGD) IGD指标反映解集的收敛性和多样性的组合信息,计算公式如下,其中,P*表示理想Pareto前沿面PFture,P表示算法迭代得到的近似Pareto前沿面PFknow,另外d(v,P)表示v到P的最小欧几里得距离.IGD指标值越小,表示算法得到的解集质量越高. (3) 2) 世代距离(GD) GD指标反映算法的收敛性,计算公式如下,其中,n为种群个数,di为算法计算得到的第i个解与PFtrue中最近解之间的欧几里得距离,GD指标值越小,表示算法迭代得到的近似Pareto前沿越逼近已知的Pareto前沿,算法的收敛性越好. (4) mHN2991003131055621083,3240102,2275测试函数m≤5m>5DTLZ115000∗m100000DTLZ21000020000DTLZ320000∗m150000DTLZ41000020000 T_num是重构邻域策略中一个重要的参数,影响精英解集的选择,为了研究潜力值评价下限T_num对算法性能的影响,重构邻域策略对T_num的敏感性,分析T_num=2,4,6,8,10,12,14,16,18,20时,在2,5,8,10维目标上对DTLZ1-4系列测试问题进行了测试,除T_num之外的所有其他参数保持一致,图3为T_num对算法收敛性分析. 从图3可以看出,对于5,8和10维目标优化问题,MOEA/D-RNS算法在DTLZ1-4系列测试问题上,T_num设置不同的值对算法收敛性影响很小;对于2维目标优化问题,MOEA/D-RNS算法在测试问题DTLZ1和DTLZ3上,T_num设置不同的值对算法收敛性影响较为明显,T_num取16时,算法在测试函数DTLZ1上收敛性较好,而在测试函数DTLZ3上的收敛性却相对要差. 综上所述,在5维和10维目标测试问题上,T_num取值不同对MOEA/D-RNS算法性能几乎没有影响;在2维目标测试问题上,T_num取值对MOEA/D-RNS算法性能影响较大;在8维目标测试问题上,T_num取值对测试问题DTLZ1影响较大,但对测试问题DTLZ2-4几乎没有影响.在我们后续的实验中,T_num设置成10. 为了验证使用重构邻域策略改变父代选择方式的MOEA/D-RNS算法性能,测试算法在ZDT1-4系列测试函数上的GD指标以及IGD指标,衡量改进算法MOEA/D-RNS收敛性和综合性能,对比结果如表3和表4所示,其中黑色加粗的数据表示对比结果中的最优值,表格中STD(Standard deviation)为30次数据的标准差. 对MOEA/D-RNS及其对比算法在 ZDT系列测试函数上的 GD 指标30次数据,每10代取平均之后绘图,GD指标随算法迭代代数变化(50-600代)的曲线如图4所示,仿真结果显示,在测试函数ZDT1(单模态的连续凸函数)上,MOEA/D-RNS在种群搜索前期,收敛速度较快,并在350代之后趋于稳定,算法优于MOEA/D、MOEA/D-DE、MOEA/D-DU;在测试函数ZDT2(单模态的连续凹函数)上,在算法收敛前期,相比于MOEA/D-DU、MOEA/D-DE和NSGA-Ⅲ,MOEA/D-RNS收敛速度较快,略差于MOEA/D;在测试函数ZDT3(多模态的不连续函数)上,MOEA/D-RNS收敛速度优于MOEA/D和MOEA/D-DU,但劣于NSGA-Ⅲ和MOEA/D-DE;在ZDT4(多模态的连续凸函数)上,由于MOEA/D-RNS加入重构邻域策略,加快种群收敛速度,使种群快速收敛到前沿面,算法显著优于MOEA/D-DU、MOEA/D-DE,略优于NSGA-Ⅲ. 图3 T_num对算法收敛性影响分析 图4 ZDT1-4 GD指标值随代数变化图 另外一方面,从图4(a)中可以看到,在ZDT1测试问题上,MOEA/D-DU算法在搜索后期出现了严重的种群退化现象,另外MOEA/D和NSGA-Ⅲ也在算法搜索过程中出现了不同程度种群退化的问题;从图4(b)中可以看到MOEA/D在种群进化过程中出现较为严重的种群退化问题.本文提出的MOEA/D-RNS有效改善了种群退化的问题,提升了算法收敛速度,从而使得算法在搜索后期将更多的计算资源用于种群多样性提升. 从表3的IGD指标对比可知,MOEA/D-RNS在测试函数ZDT1和ZDT2上综合性能显著优于其他对比算法;在测试函数ZDT3上,MOEA/D-RNS显著优于MOEA/D-DE、NSGA-Ⅲ和MOEA/D,略优于MOEA/D-DU;在测试函数ZDT4上,MOEA/D-RNS显著优于MOEA/D-DU、MOEA/D-DE和MOEA/D,略优于NSGA-Ⅲ.说明加入了重构邻域策略的MOEA/D-RNS能有效改善解集的分布性和算法收敛性,因此相比于对比算法,MOEA/D-RNS算法求得的IGD指标值更优. 表3 ZDT1-4系列测试函数在IGD指标上的测试结果对比 Table 3 Test results Comparison of IGD indicator on ZDT1-4 test Functions fMOEA/D-RNSMOEA/D-DUNSGA-IIIMOEA/D-DEMOEA/DMean(STD)Mean(STD)Mean(STD)Mean(STD)Mean(STD)ZDT14.3423e-3(8.17e-4)9.2061e-3(8.29e-3)6.8310e-3(9.52e-3)1.1428e-2(5.13e-3)1.1316e-2(7.85e-3)ZDT24.3423e-3(8.17e-4)5.9653e-2(9.41e-2)5.6148e-3(4.73e-3)9.6273e-3(3.32e-3)5.9777e-2(8.52e-2)ZDT31.0901e-2(5.14e-5)1.6811e-2(1.16e-2)4.3523e-2(5.72e-2)3.2702e-2(1.97e-2)2.9379e-2(2.18e-2)ZDT46.0437e-3(1.26e-3)2.4126e-2(1.62e-2)8.9931e-3(7.75e-3)2.1496e-2(1.20e-2)2.1707e-2(1.17e-2) 表4 ZDT1-4系列测试函数在GD指标上的测试结果对比 Table 4 Test results comparison of GD indicator on ZDT1-4 test functions fMOEA/D-RNSMOEA/D-DUNSGA-IIIMOEA/D-DEMOEA/DMean(STD)Mean(STD)Mean(STD)Mean(STD)Mean(STD)ZDT12.8703e-5(7.47e-6)1.8626e-4(5.40e-5)9.3503e-5(3.25e-5)1.0476e-3(5.25e-4)4.8025e-4(2.57e-4)ZDT23.8861e-5(4.97e-5)6.8304e-4(3.97e-4)7.4041e-5(3.03e-5)9.5857e-4(5.85e-4)8.0239e-4(5.73e-4)ZDT36.5362e-5(8.82e-5)2.7251e-4(8.99e-5)6.5537e-5(2.39e-5)1.5133e-3(9.70e-4)1.0193e-3(1.75e-3)ZDT42.7852e-4(1.71e-4)2.1187e-3(2.15e-3)2.8415e-4(2.01e-4)2.8782e-2(2.70e-2)2.9316e-3(3.12e-3) 为了进一步验证重构邻域策略在高维目标优化问题上的算法性能,采用GD、IGD指标衡量MOEA/D-RNS及四种对比算法在2-10维目标上的整体性能,对DTLZ1-4系列测试函数均运行30次并取平均值作为最终的测试值,测试结果如表5、表6所示. 表5 DTLZ1-4系列测试函数在IGD指标上测试结果对比 Table 5 Test results comparison of IGD indicator on DTLZ1-4 test functions fMMOEA/D-RNSMOEA/D-DUNSGA-ⅢMOEA/D-DEMOEA/DMean(STD)Mean(STD)Mean(STD)Mean(STD)Mean(STD)DTLZ121.9512e-3(2.26e-4)1.9295e-3(2.20e-4)2.1353e-3(4.26e-4)2.3197e-3(1.92e-3)2.8352e-3(8.26e-4)31.9188e-2(1.57e-4)1.9197e-2(1.47e-4)1.9084e-2(1.22e-4)8.8421e-2(1.40e-1)1.9610e-2(5.20e-4)55.2793e-2(1.16e-4)5.3840e-2(6.01e-4)5.3074e-2(3.83e-4)7.1506e-1(5.94e-1)1.1173e-1(2.63e-4)89.0471e-2(2.56e-4)9.0463e-2(3.63e-4)1.0803e-1(3.53e-2)1.4081e-1(3.61e-3)1.5170e-1(2.75e-3)101.2216e-1(1.85e-3)1.2312e-1(1.87e-3)1.3706e-1(3.69e-2)3.4944e-1(2.32e-1)1.8269e-1(2.08e-2)DTLZ224.0691e-3(5.25e-5)4.1392e-3(7.48e-5)4.1707e-3(9.41e-5)4.1274e-3(4.73e-5)4.3403e-3(1.36e-4)35.3848e-2(8.33e-4)5.4779e-2(1.20e-3)5.1141e-2(1.93e-4)7.1479e-2(1.05e-3)6.7963e-2(6.39e-4)52.0134e-1(4.72e-3)2.0712e-1(4.95e-3)1.8589e-1(5.13e-3)4.3386e-1(3.22e-2)3.1804e-1(1.94e-3)83.1974e-1(1.16e-3)3.2095e-1(1.64e-3)3.3053e-1(4.19e-2)5.6291e-1(1.95e-2)5.4157e-1(1.31e-3)104.7920e-1(4.17e-3)4.9317e-1(4.01e-3)5.3919e-1(1.15e-1)7.1579e-1(4.67e-2)6.8061e-1(2.32e-2)DTLZ327.9587e-3(3.17e-3)6.4780e-2(2.13e-1)1.5401e-2(1.20e-2)2.4912e+0(4.14e+0)2.4025e-2(1.28e-2)35.2807e-2(1.25e-3)6.5839e-2(1.89e-2)5.3366e-2(3.87e-3)3.7475e+0(8.18e+0)3.5268e-1(6.75e-1)51.9411e-1(1.28e-2)4.0842e-1(3.87e-1)5.6281e+1(1.27e+1)1.4031e+1(1.38e+1)7.5186e-1(1.75e+0)83.1698e-1(1.10e-3)3.1851e-1(2.93e-3)5.0716e-1(6.02e-1)2.2590e+0(4.10e+0)5.5711e-1(8.13e-2)104.5369e-1(3.72e-3)4.7742e-1(1.21e-2)2.3889e+0(2.81e+0)7.8227e+0(1.23e+1)7.3956e-1(6.28e-2)DTLZ424.0866e-3(4.92e-5)4.1426e-3(6.87e-5)1.2722e-1(2.80e-1)6.0954e-3(1.66e-3)1.7760e-1(3.17e-1)35.4751e-2(1.14e-3)5.6133e-2(1.35e-3)1.4646e-1(2.27e-1)1.9102e-1(6.57e-2)5.2151e-1(3.12e-1)51.9359e-1(3.27e-3)2.0830e-1(2.88e-3)2.1819e-1(7.83e-2)4.3733e-1(2.92e-2)5.1677e-1(2.26e-1)83.3278e-1(2.50e-3)3.3783e-1(2.31e-3)3.6237e-1(6.37e-2)6.5478e-1(4.03e-2)6.4785e-1(1.66e-1)104.5202e-1(6.49e-4)4.5473e-1(1.21e-3)5.0502e-1(5.26e-2)7.6172e-1(3.20e-2)7.3044e-1(1.01e-1) 4.5.1 算法综合性能(IGD)分析 从表5所示的IGD指标测试结果来看,在测试函数DTLZ2、DTLZ3和DTLZ4上,MOEA/D-RNS在表中所给的所有目标维度优化问题上严格优于所有对比算法;在测试函数DTLZ1上,对于3、5和10维目标优化问题,MOEA/D-RNS优于所有对比算法,但对于2、8维这两个目标优化问题,MOEA/D-RNS综合性能(IGD)优于MOEA/D-DE、MOEA/D和NSGA-Ⅲ,但劣于MOEA/D-DU. 说明在高维目标优化问题上,重构邻域策略能得到更高质量的解集,使种群更快收敛到近似Pareto前沿面,能更好平衡算法收敛性和解集分布性,改善算法整体性能. 4.5.2 解集收敛性分析 表6 DTLZ1-4系列测试函数在GD指标上测试结果对比 Table 6 Test results comparison of GD indicator on DTLZ1-4 test functions fMMOEA/D-RNSMOEA/D-DUNSGA-ⅢMOEA/D-DEMOEA/DMean(STD)Mean(STD)Mean(STD)Mean(STD)Mean(STD)DTLZ125.3127e-5(4.70e-5)4.9548e-5(4.45e-5)8.6408e-5(7.32e-5)8.9595e-5(2.19e-4)1.7180e-4(1.22e-4)32.1613e-4(5.16e-5)2.1456e-4(4.07e-5)2.0437e-4(3.91e-5)1.4580e-2(3.61e-2)5.7574e-4(1.61e-4)59.6515e-4(1.96e-5)9.8608e-4(1.73e-4)1.0471e-3(1.84e-5)1.2707e+0(5.03e-1)1.0903e-3(2.35e-5)81.5151e-2(4.58e-2)5.9758e-2(1.20e-1)3.5133e-2(8.87e-2)8.9715e-2(8.93e-2)3.1293e-2(5.94e-2)102.1892e-3(1.20e-4)2.2725e-3(9.80e-5)1.7131e-1(2.68e-1)4.0333e-1(2.82e-1)2.8703e-3(1.13e-4)DTLZ221.7153e-5(4.33e-6)2.6257e-5(5.49e-6)5.0440e-5(1.38e-5)7.0171e-5(9.58e-6)2.6100e-5(1.97e-5)34.6578e-4(1.94e-5)4.6858e-4(1.78e-5)6.5389e-4(4.68e-5)1.6326e-3(1.95e-4)6.8120e-4(6.21e-5)52.8013e-3(6.27e-5)3.2696e-3(2.20e-4)5.9351e-3(6.42e-4)1.6477e-2(2.80e-3)3.8768e-3(2.48e-4)89.4810e-3(6.26e-4)1.0507e-2(2.93e-4)1.3150e-2(7.67e-4)1.7856e-2(1.41e-3)1.6602e-2(1.68e-4)105.3196e-3(4.35e-4)5.7067e-3(5.00e-4)1.1947e-2(1.52e-3)1.8114e-2(1.58e-3)9.6151e-3(3.91e-4)DTLZ325.9767e-4(3.83e-4)1.0681e-2(3.46e-2)2.8292e-3(9.29e-3)5.4706e-1(9.74e-1)8.0034e-4(1.58e-3)37.6258e-4(2.37e-4)4.3217e-3(9.76e-3)1.2808e-3(7.52e-4)5.5718e-1(1.24e+0)4.2392e-2(9.00e-2)53.6635e-3(2.63e-3)3.9711e-2(4.86e-2)1.2597e+1(1.81e+0)7.1299e+0(1.90e+0)8.4046e-2(2.38e-1)81.2013e-2(1.06e-4)9.0417e-2(1.87e-1)2.8297e-1(6.33e-1)6.0520e-1(1.19e+0)1.8357e-2(1.37e-3)106.2853e-3(2.59e-4)1.0985e-2(1.25e-2)1.9017e+0(2.20e+0)2.8382e+0(2.27e+0)1.4387e-2(1.88e-3)DTLZ421.8463e-5(4.12e-6)2.9708e-5(5.77e-6)5.0329e-5(2.23e-5)1.8521e-4(1.27e-4)5.4556e-5(1.50e-4)34.5385e-4(1.92e-5)4.6494e-4(1.86e-5)6.0539e-4(1.56e-4)1.2740e-3(6.62e-4)3.1899e-4(2.13e-4)52.8130e-3(4.99e-5)2.9555e-3(8.82e-5)6.2451e-3(8.39e-4)5.3922e-3(1.28e-3)2.9445e-3(7.68e-4)89.0966e-3(2.20e-4)8.6040e-3(2.08e-4)1.2813e-2(1.04e-3)7.9923e-3(6.97e-4)8.8173e-3(2.89e-3)104.0594e-3(3.01e-4)4.1642e-3(3.17e-4)1.2839e-2(3.27e-3)6.5094e-3(1.82e-3)4.9143e-3(8.13e-4) 从表6的GD指标测试结果来看,在测试函数DTLZ1上,对于5、8、10维目标优化问题,MOEA/D-RNS均优于其他四种对比算法,对于2、3维目标优化问题,MOEA/D-RNS优于NSGA-Ⅲ、MOEA/D-DE和MOEA/D,略差于MOEA/D-DU.在测试函数DTLZ2和DTLZ3上,MOEA/D-RNS对于2-10维目标优化问题均优于所有对比算法.在测试函数DTLZ4上,对于2、5、10维目标优化问题,MOEA/D-RNS严格优于其他对比算法;对于3维目标优化问题,MOEA/D-RNS优于MOEA/D-DU、NSGA-Ⅲ和MOEA/D-DE,但劣于MOEA/D;对于8维目标优化问题,MOEA/D-RNS优于NSGA-Ⅲ,劣于其他对比算法. 这是由于测试函数DTLZ1及DTLZ3属于复杂多模态测试函数,并且在目标空间中,初始种群离真实Pareto前沿面较远,算法收敛到近似Pareto前沿所需迭代代数较多,在这类测试函数上,MOEA/D-RNS算法重构邻域策略算法搜索过程中加快种群收敛的效果较为明显,MOEA/D-RNS算法重构邻域策略在整个种群中挑选精英解集,在精英解集和邻域子集组成的新邻域中挑选父代,使整个种群都尽可能地与优秀的个体进行交叉变异,进而改善后代解集的质量,从而加速种群收敛.特别是在测试函数DTLZ3上,对于2、3、5、10维目标优化问题,MOEA/D-RNS算法GD指标值远远优于其他对比算法,说明在此测试函数上,改进算法MOEA/D-RNS加快种群收敛速度和改善种群退化状况效果较为显著. 通过ZDT1-4和DTLZ1-4系列测试问题分析说明:加入了垂直距离更新策略的MOEA/D-DU与MOEA/D-RNS相比于MOEA/D-DE、MOEA/D和NSGA-Ⅲ这三种对比算法,能够有效改善算法在高维目标优化问题中解偏离搜索方向的问题,有效平衡算法的收敛性与多样性.MOEA/D-DU在搜索过程中存在种群退化的问题,加入了重构邻域策略的MOEA/D-RNS有效解决此问题,使得种群更快逼近Pareto前沿面,提升了算法收敛速度,从而也使得在算法搜索过程中有更多的计算资源用于提升种群多样性. 本文结合垂直距离更新策略,提出了一种分两步筛选精英解集的方式,在不改变邻域规模的前提下改变了交叉变异操作中的父代选择方式,改善了父代解集质量,加快了种群收敛到Pareto前沿的速度,保持种群多样性,提高了算法整体性能.测试结果表明使用了重构邻域策略的MOEA/D-RNS,在初始种群距离已知的Pareto前沿面较远时收敛效果显著,同时保证了解集的多样性,并且在高维目标优化问题上重构邻域策略仍能较好的提升算法整体性能.重构邻域策略不仅在MOEA/D-DU上适用,在其他分解算法上仍能对算法有较好的性能提升效果.4 仿真实验及分析
4.1 参数设置
4.2 算法性能评价指标

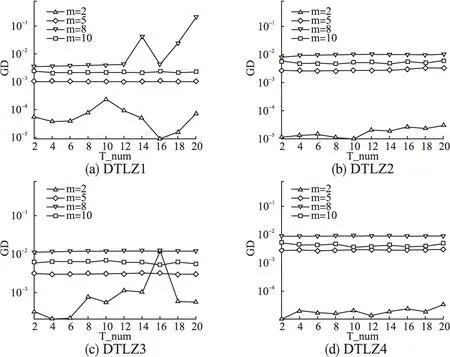
4.3 参数T_num影响分析
4.4 ZDT1-4系列测试问题性能分析
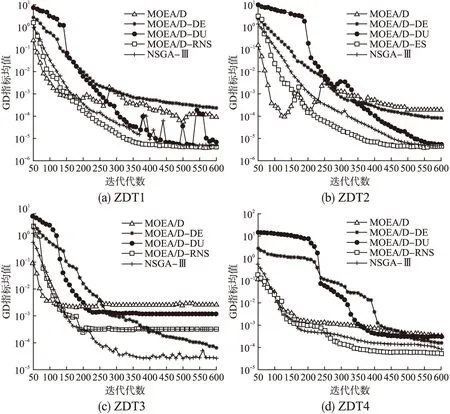


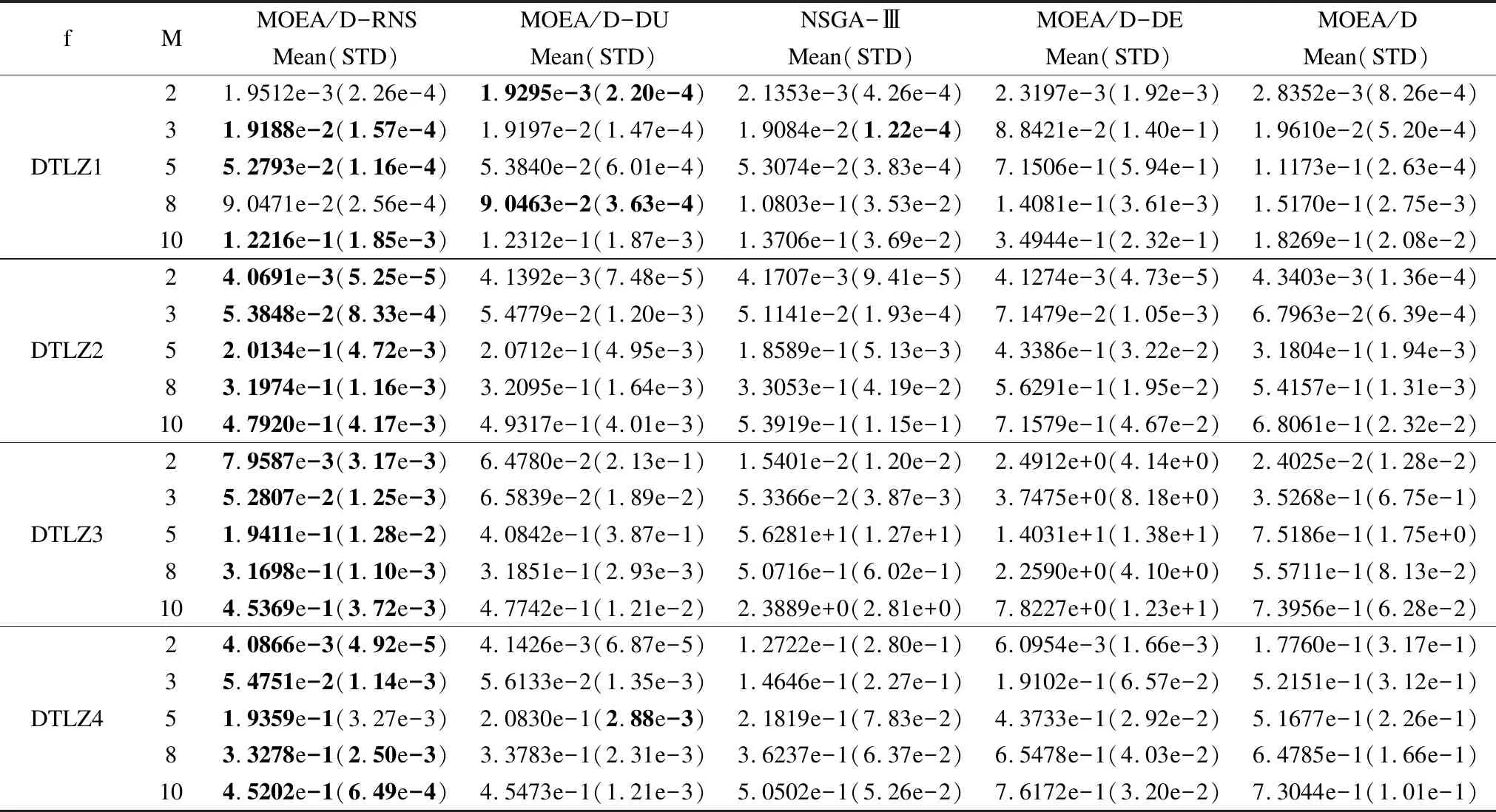
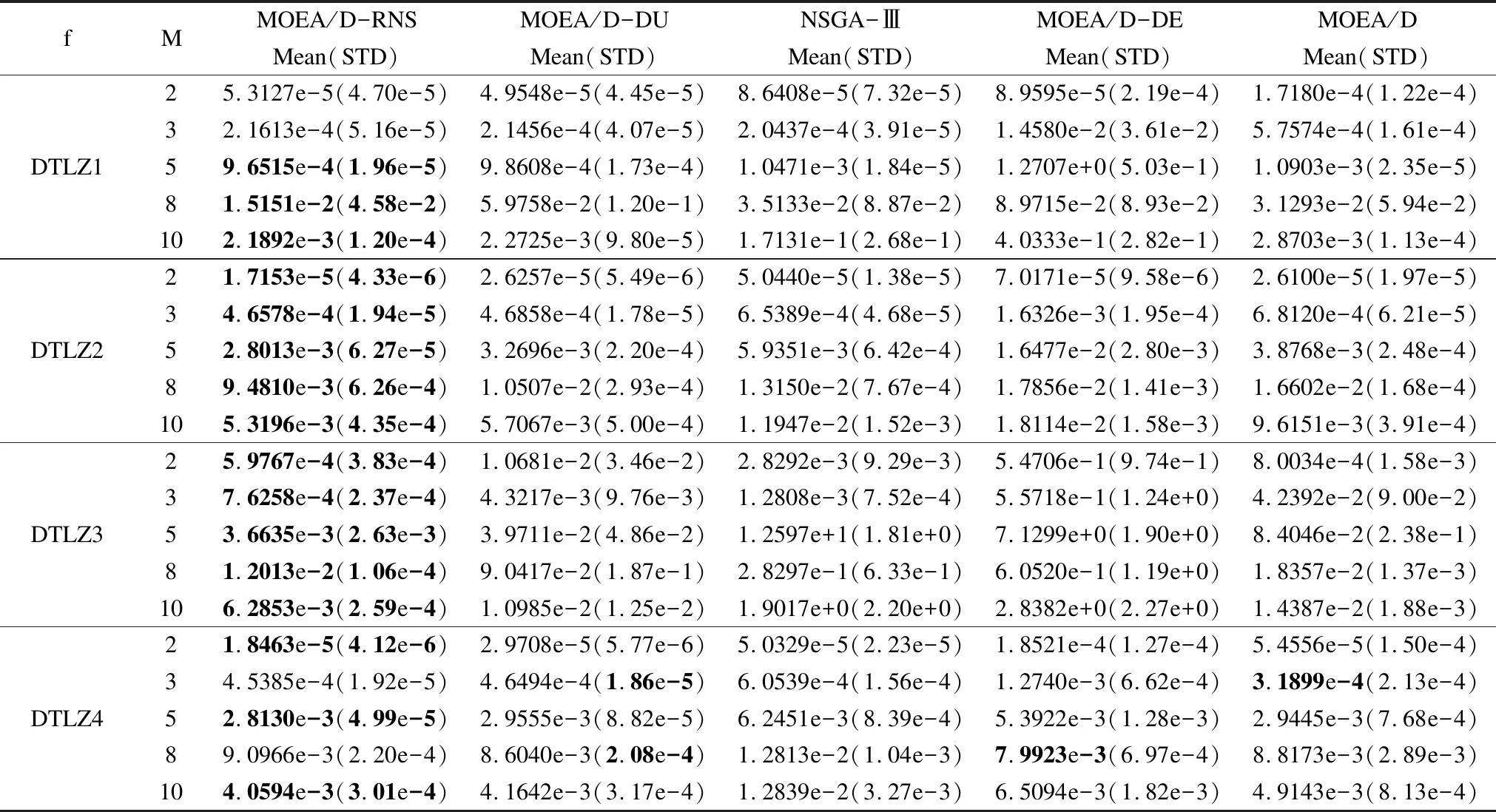
4.5 DTLZ1-4系列测试问题性能分析
4.6 策略有效性分析
5 总 结
