基于区块链的公钥可搜索加密方案

杜瑞忠，谭艾伦，田俊峰

（1.河北大学网络空间安全与计算机学院，河北 保定 071002；2.河北省高可信信息系统重点实验室，河北 保定 071002）

1 引言

云存储是当下一种主流的在线存储方式，在免去用户本地存储的硬件与管理开销的同时，使数据脱离了用户的物理控制，因此数据的安全受到了巨大威胁。为了解决云存储的数据安全问题，一般采用数据加密的方式，但是加密后的数据在云服务器中会面临检索困难的问题。

安全搜索通常指对加密数据的有效搜索，为了解决加密数据存储在云端时，服务器在不完全可信的前提条件下如何利用服务器来完成安全的关键字搜索问题，学者们提出了将可搜索加密作为安全搜索的核心技术。

可搜索加密是一种支持用户在密文中进行关键字检索的新技术，主要解决云存储环境下如何利用不可信服务器实现基于关键字的安全搜索，使用户能够将加密的数据存储到云中，并通过密文域来执行关键字搜索，有选择地从云中检索感兴趣的文档。

2 相关工作

2000 年，Dawn 等[1]为了增强数据在服务器上的安全性，提出一对一模式的可搜索加密方案，从此引发人们对可搜索加密的研究。由于一对一的模式不能满足人们的需求，Boneh 等[2]于2004 年提出多对一的模式可搜索加密模型，给出了基于公钥的可搜索加密（PEKS,public key encryption with keyword search）的概念，并定义了公钥加密下可搜索加密的安全性。但在某些特性的环境下，多对一模式并不实用。2011 年，Curtmola 等[3]基于Naor 广播加密技术构造出一对多的可搜索加密模型，但是该模型中用户密钥更换时需要极大的开销。在大型网络环境中，数据的传输是复杂的，Wang 等[4]基于Shamir 的秘密共享技术和文献[2]中基于身份的加密技术构造了多对多模式的加密方案，实现了多用户在服务器中的交互式检索。Yuan 等[5]为了有效地解决多接收者时变密文的检索问题，提出了一种一对多公钥密文时间释放可搜索加密（PKTRSE_(OM)）的密码模型，在PKTRSE_(OM)模型中，发送方将加密消息发送给云服务器，只有预定的授权用户组成员才能搜索到包含指定关键字的目标密文，但是直到将来发布时才能解密。Zhong 等[6]提出一种多对一的同态加密方案，克服了传统同态加密一对一的局限性。

在可搜索加密方案的安全性方面，Boneh 等[2]证明了公钥可搜索加密是基于语义安全的，但却不能抵御关键字猜测攻击（KGA,keyword guess attack）。2009 年，Tang 等[7]提出了一种基于公钥加密的注册关键字搜索方案，该方案可以抵御KGA，但是必须预先注册关键字，这使方案性能并不高。2013 年，Fang 等[8]提出一种可以抵御关键字攻击的公钥加密方案，该方案定义了一个公钥可搜索加密模型和2 个重要的安全概念。这2 个安全概念中，一个针对内部攻击，另一个针对外部攻击，但是大量的双线性配对计算导致Fang 等[8]方案的效率较低。

近年来，在内部攻击方面，学者们进行了很多研究。2013 年，Xu 等[9]提出了带有2 个陷门（模糊陷门和精确陷门）的方案，并称该方案可以抵抗内部KGA。在该方案中，敌手只能获得模糊陷门，因此无法提取关于陷门对应关键字的确切信息，受到了安全性和效率方面的限制。2015 年，Chen 等[10]引入了一种新的框架以防止内部KGA，该框架使用2 个服务器，并要求2 个服务器不能相互“勾结”。但是，任何人都可以生成关键字的合法陷门，这将影响数据的隐私安全。Shao 等[11]提出并解决了服务器进行离线 KGA 的问题，重新定义了 dPEKS（designated tester public key encryption with keyword search）对KGA 的安全性并提出了IND-KGASERVER 安全性，根据公钥基础设施证书颁发机构和确定性数字签名的存在情况，演示当KGA 攻击者是服务器时如何构造安全的dPEKS。2016 年，Chen 等[12]提出一种使用2 个云服务器的方案来抵御内部KGA，并且方案具有较高的效率，但是由于假设条件中要求2 个云服务器不能串联，这在实践中很难实现。2017 年，Huang 等[13]基于关键字搜索提出了一个公钥认证加密方案，该方案的密文生成过程中需要数据所有者的密钥，虽然方案可以抵抗内部KGA，但无法实现所选关键字密文的不可区分性。Kang 等[14]提出一种利用双线性对和TF/IDF（term frequency/inverse document frequency）算法构成的完全安全的公钥加密方案，该方案在静态假设条件下达到了安全，与传统的可搜索加密方案相比，该方案在可搜索效率、密文完整性和安全性方面有较好的性能。2018 年，Wu 等[15]提出了一种高效安全的、具有隐私保护的可搜索公钥加密方案，该方案使用了Diffie-Hellman 共享密钥，并被证明能够抵抗KGA。

在最新的研究成果中，公钥可搜索加密被运用于各种环境，Wu 等[16]在物联网环境中，提出了一种无证书的可搜索公钥认证加密方案，在能抵御KGA 的同时，也具有较高的效率。Ma 等[17]设计了一种新的基于多关键字的无证书公钥加密方案，用于IoT（Internet of things）部署。Lu 等[18]针对电子病历系统，提出了2 种安全的无信道PEKS 方案，后来经过证明，2 种方案都存在由KGA 引起的安全漏洞。针对这一问题，Lu 等[18]又提出了一种新的PEKS 方案，该方案不仅能抵抗现有的3 种类型的关键字猜测攻击，还改善了指定服务器的缺点。

随着区块链的发展，可搜索加密与区块链技术相结合，解决了传统方案中可信第三方的问题，极大地提高了可搜索加密的可实现性。Li 等[19]提出了一种基于区块链的对称可搜索加密方案，该方案不仅提出了基于区块链的可搜索加密模型，还针对不同大小的数据提出了2种方案。2019年，Li 等[20]对文献[19]的方案进行了改进，提高了可实现性。Chen 等[21]基于区块链机制提出了一个用于电子医疗记录分享的可搜索加密方案，该方案同样通过对称加密的方法，使用智能合约作为方案中的权威可信方，保证方案中服务器的可信度。

针对现有方案中第三方的可信问题，本文引入区块链，构建区块链环境下的公钥可搜索加密方案，旨在解决私有云环境中一对多的数据分享问题。本文的主要贡献如下。

1)在密文检索方案中引入区块链机制，利用区块链解决传统方案中第三方的可信问题；将检索工作放到区块链中进行计算，保证检索结果的正确性；利用区块链的不可篡改性，对文件进行编号，防止在云服务器错误时发送数据，或恶意发送错误的数据。

2)针对私有云环境，构造一对多的公钥可搜索加密方案。该方案中使用DBDH（decisional bilinear Diffie-Hellman）困难问题的构建方式，使同一个关键字多次加密结果不同，可以有效抵御KGA，保证索引及陷门不会泄露关键字信息。

3)对所提方案进行安全性证明，验证了方案可抵御KGA，同时分析区块链的安全性在方案中的作用。本文基于PBC（pairing based cryptography）库环境，在数据集上进行实验，得出方案的索引与陷门构造以及查询时间，证明了所提方案具有较高的效率。

3 预备知识

3.1 双线性映射

假设群G与群GT是阶为素数p的循环群，g是群G的生成元，存在双线性映射并满足以下性质。

1)双线性。对任意的x,y∈G，a,b∈GT，存在。

2)非退化性。存在g∈G，使。

3)可计算性。对所有的x,y∈G，存在有效的算法来计算ê(x,y)。

3.2 判定性双线性Diffie-Hellman 假设

设群G1、G2及双线性映射，g是群G1的生成元，随机生成(a,b,c,z)←RZp，生成2 个五元组T0=(g,A=ga,B=gb,C=gc,Z=eˆ(g,g)z)与T1=(g,A=ga,B=gb,C=gc,Z=eˆ(g,g)abc)。其中，a、b、c、z表示所生成的随机数，RZp表示随机的实数空间将2 个五元组分别记为

DBDH 假设指没有多项式时间的敌手，能以不可忽略的优势ε来区分五元组PBDH与RBDH。

3.3 智能合约

智能合约是一种旨在以数字方式执行合同谈判的计算机程序。智能合约与传统合同不一定相同，可以是任何类型的计算机程序，利用加密算法和各种安全协议，实现不同类型的智能合约。智能合约有助于交易的可靠执行，而不涉及某些第三方，并且所有交易都是可追踪和不可逆转的。换句话说，智能合约提供的安全性优于传统的合同，并降低了与合同相关的交易成本。

以太坊是一个运行智能合约的分散式平台。在以太坊中，智能合约用于在区块链上执行一些通用计算。由于区块链的特性，所有操作在以太坊中都是透明和可靠的，这意味着理论上可以使用以太坊智能合约来执行任何计算任务。

3.4 符号及其含义

本文的符号及其含义如下。

Cm：对明文m对称加密后的密文。

H：哈希函数h对密文C与编号密文N的运算结果。

I：数据文件索引。

k：对称加密密钥。

N：私钥加密后的文件编号。

Tw：关键字陷门。

Twi：索引中的关键字陷门。

w：文件中的关键字。

wi：用户查询的关键字，i=1,2,…,I。

$offer：检索单价。

$user：用户账户。

$deposit：押金账户。

4 系统模型

4.1 系统简介

本文具体系统主要由4 个部分组成：数据拥有者（DO,data owner）、云服务器（CS,cloud server）、智能合约（smart contract）、用户（U,user）。系统模型及其流程如图1 所示。

1)数据拥有者。主要工作是计算索引和密文数据，然后将索引上传给智能合约，将密文数据上传给云服务器。

2)云服务器。主要工作是存储由数据拥有者上传的密文数据，接收由用户上传的数据下发请求，并与智能合约进行交互，得到下发验证结果。

3)智能合约。主要工作是接收数据拥有者上传的索引与用户上传的陷门，并且进行查询，得到查询结果，通过交易将结果下发给用户。然后通过与服务器的交易，告知服务器是否下发密文。

4)用户。主要工作是计算陷门，并上传给智能合约，同时向服务器发送密文请求，最后得到数据并解密。

4.2 算法定义

1)setup(1λ)→par 。系统初始化由安全参数λ生成公开参数par。

2)Enc(n,m,w,k)→(CT,I,N)。该算法由数据拥有者计算，由明文数据m与对称加密密钥k，以及文件中的关键字w生成密文Cm与数据文件索引I。其中明文m与对称加密密钥k加密后得到密文Cm，加密关键字w时会将密钥k一起加密，生成索引I。将明文进行编号，每个编号n使用对称加密后得到密文状态下的编号数据N。最后使用哈希函数对N和Cm进行计算得到结果H，将N、H打包后得到CT。

3)T(wi)→Twi。该算法由用户进行计算，用户选取文件中的关键字w，加密计算后得到关键字陷门Tw，并将Tw上传给智能合约。

4)search(I,Twi)→(k,N,H)。该算法由智能合约进行计算，智能合约在接收到Tw与I后进行计算，若匹配成功，则得到明文的对称加密密钥k、编号密文N及哈希结果H。

5)verify(CT,N)→0或1。该算法由用户进行计算。用户收到服务器下发的密文CT以后，需要验证服务器是否错误下发密文以及是否恶意破坏或者篡改密文数据。首先验证CT中文件编号N与H是否同智能合约下发的一致，然后将Cm与N进行哈希运算，得到结果H1，若H=H1，则验证成功，输出1，否则输出0。

4.3 安全模型

4.3.1 关键字隐私安全游戏

如果不存在敌手A 能够在概率多项式时间内从密文关键字或陷门值推断出关键字明文信息，则关键字的隐私安全可以得到保证。定义关键字隐私安全游戏如下。

1)初始化。给定安全参数λ，挑战者C 执行初始化算法Init(lλ)，生成par。

2)阶段1。敌手A 多次运行陷门生成算法。

3)挑战。敌手A 从关键字空间随机选取2 个关键字，发送给挑战者，挑战者执行陷门生成算法，然后随机选取一个陷门发送给敌手A。

图1 系统模型及其流程

4)猜测。敌手A 查询了τ个不同的关键字后，进行分析猜测，如果敌手能够猜对陷门，则敌手A在安全游戏中获胜。

4.3.2 判定性双线性Diffie-Hellman 假设困难问题规约证明

如果存在敌手A 能够在多项式时间内以优势б破解方案，则敌手A 能在多项式时间内以优势б解决 DBDH 困难问题。定义判定性双线性Diffie-Hellman 假设困难问题规约证明如下。

1)初始化。给定群组G1、G2及映射。挑战者C随机生成（a,b,c,z）←RZp，生成2 个五元组T0、T1。

2)阶段1。敌手A 多次运行加密算法。

3)挑战。挑战者C 随机选取明文m，要求m在阶段1 未被查询，并生成密文Cm，将密文传给敌手A。

4)猜测。敌手A 对密文Cm进行分析解密，如果敌手A 能够解密密文Cm且得到正确的明文m，则敌手A 在游戏中获胜。

5)证明。敌手A 能够对密文进行解密，则敌手A 也能解决判定性双线性Diffie-Hellman 假设困难问题。

5 具体系统描述

1)初始化阶段

Setup(1λ)→par 。系统初始化，由安全参数λ生成公开参数par，其中包括循环群G、GT；g是群G的生成元，g1是群G的元素；哈希运算h，随机参数a；计算得到g2=ga；双线性映射。

智能合约初始化，数据拥有者设置检索单价$offer。用户使用ID 注册账户$user 并存款，区块链系统设置押金账户$deposit。

2)密文加密与上传

Enc(m,w,k)→(Cm,I)。明文m由对称加密密钥k经过加密得到密文Cm，然后将对称加密密钥k加入索引I的计算过程中。首先选择一个随机数r←RZP，然后将文件的关键字w进行哈希运算得到H(w)，计算后得到

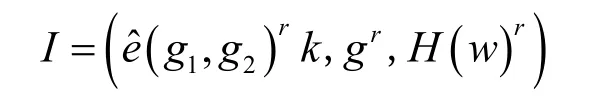
数据拥有者将加密后的密文Cm与索引I进行编号，并将编号使用私钥进行加密，得到密文状态的文件编号N，将文件编号N与密文Cm存储在一起后进行哈希运算得到结果H，将文件编号N、结果H打包为密文CT。将文件编号N和密文Cm上传给服务器进行存储操作，将打包的密文CT与索引I上传给智能合约进行查询操作。

3)陷门加密与上传

T(wi)→Twi。用户计算得到索引文件中的关键字w的陷门Twi。首先将文件中的关键字进行哈希运算得到H(w)，再选择一个随机数t←RZP，计算得到

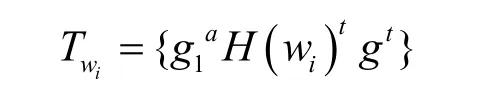
用户上传陷门到智能合约，并由自身账户余额向区块链系统进行存款操作$user→$deposit。

4)查询阶段

search(I,Twi)→k。智能合约通过交易来接收用户的索引I，检查用户ID 是否合法。然后系统检查押金账户$deposit 中用户预存的押金是否满足一次搜索，当押金满足时将陷门和数据文件索引进行计算，计算过程如下

如果w=wi，则最后的结果为对称加密密钥k，智能合约将会记下文件编号N，然后开始下一次的查询，直到所有的文件都检索完毕。

5)验证阶段

verify(CT,N)→ 0或者 1。智能合约在已经检索出的文件集中进行下一个关键字的检索操作，同时从押金账户中扣去对应的检索单价$offer，直到押金账户$deposit 的金额不足以进行一次检索，区块链系统就会返回用户押金不足信息：$deposit←$deposit-$offer。

如果押金账户中的金额能够满足用户上传的所有关键字的检索操作，智能合约将所有满足用户关键字请求的文件编号N以及用户ID 发送给云服务器，云服务器接收后，根据文件编号N将密文Cm下发给用户。

同时在智能合约与用户的数据交互过程中，智能合约检索成功后得到密文CT与对称加密密钥k，然后发送给用户，用户验证NBS=NCS。其中，NBS表示区块链系统发送的文件编号，NCS表示云服务器发送的文件编号。

若从服务器与智能合约接收的文件编号相同，则证明服务器没有错误下发数据，然后验证

将密文Cm与文件编号N进行哈希运算，若得到的结果H1与CT中的H相等，则证明服务器没有对密文数据进行篡改，最后用密钥k对密文Cm进行解密，得到明文m。

6 安全性分析

将检索过程放在区块链系统中运行，可以保证以下几个方面的安全。

1)公正性。由于区块链与每个用户进行交互时都在基于交易的基础上，每次交易都是透明的，那么可以保证每次查询的结果是正确的，且不会存在恶意篡改结果的情况。同时由于每次交易需要一定的费用，可以有效地防止恶意用户破坏方案正常工作的情况。

2)可信性。区块链给出的检索结果一定是诚实可信的，同时也能以这个结果为基准，有效地防止恶意服务器对本文方案造成的威胁。用户可以有效地验证服务器操作的正确性，从而获得正确的检索文件。

3)安全性。本文方案能够保证关键字的安全性，由于关键字陷门是随机加密的，因此满足IND-KGA安全。此外，由于关键的数据文件索引I的构造是按照判定性双线性Diffie-Hellman 假设困难问题中的五元组的构造方式来进行的，密文的安全性可以规约为判定性双线性Diffie-Hellman 假设困难问题。

定理1基于一般的双线性群，本文方案在随机预言模型下是满足 IND-KGA（indistinguish keyword guess attack）安全的。

初始化挑战者C 生成随机数a,b←RZP，公开参数。

1)阶段1。敌手选取关键字集合(w1,w2,…,wn)，发送给挑战者C，挑战者输出关键字集合生成的陷门集合，并发送给敌手A。

2)挑战1。敌手A 随机选取2 个关键字w0、w1，并要求w0、w1没有在第一阶段被查询过。然后将2 个关键字发给挑战者。挑战者选择随机数p，运行陷门生成算法，计算，然后选取随机数μ←(0,1)λ，将Twμ发送给敌手A。

3)猜测。敌手A 对阶段1 与阶段2 中查询的关键字陷门进行分析，输出μ'，如果μ'=μ，则敌手A 赢得游戏。

证明本文方案是支持关键字隐私安全的，由于关键字陷门在加密时引入了随机数，导致同一个关键字生成的陷门不同，可有效抵御统计分析攻击。敌手 A 在安全游戏中获胜的概率最多是。其中，n表示关键字集的个数，ε表示在安全参数λ下可以忽略的概率，Ψ表示关键字的空间。

证毕。

定理2基于一般的双线性群，本文方案的安全性可以规约到判定性双线性Diffie-Hellman 假设困难问题。如果敌手A 能够在多项式时间内以优势б破解方案，则敌手A 能在多项式时间内解决DBDH 困难问题。

初始化建立系统，生成安全参数λ，然后运行算法setup(1λ)，得到安全参数par。

1)阶段1。敌手A 多次运行索引加密算法。

2)挑战1。挑战者C 选取2个密钥k1和k2，要求它们在阶段1 不能被敌手A 查询。运行加密算法，同时生成随机数t，计算得到。然后挑战者C 随机发送一个索引I*给敌手A。

3)猜测。敌手A 收到索引I*以后，对密文进行分析解算。然后敌手输出猜测的结果I'，如果I'=I*，则敌手A 赢得游戏。如果敌手A 能够对密文I'进行正确解密，那么敌手A 就能区分密文I'中的。

4)阶段2。敌手A 尝试破解判定性双线性Diffie-Hellman 假设中的2 个五元组。敌手A 多次运行算法计算这2 个五元组。

5)挑战2。挑战者C 随机选择(a,b,c,z)←RZP，生成2 个五元组，T0是BHD 五元组，T1是随机五元组，具体如下。

挑战者C 随机生成μ←R{0,1}，若μ=0，则输出T0，若μ=1，则输出T1。挑战者将得到的五元组发送给敌手A。组T*进行分析，然后输出μ´，如果μ´=μ，则敌手A 在游戏中获胜。

6)猜测。敌手A接收到挑战者C发出的五元

证明敌手A 能够对索引I进行解密，则敌手A能够解决判定性双线性Diffie-Hellman 假设困难问题。综上所述，方案的密文安全性可以规约到判定性双线性Diffie-Hellman 假设困难问题。

证毕。

7 实验分析

实验环境为64 bit Windows 操作系统、Intel®Core(TM)i5-4570 CPU 3.20 GHz、内存16 GB，本文实验主要利用本地的虚拟机VMware 加载开源项目OpenStack 来进行性能测试，使用C++语言，加密函数由PBC 函数库提供。

本节实验将本文方案与文献[12-13,15]这3 种方案进行对比，分别对比了陷门生成时间、索引生成时间和关键字检索时间。实验中的关键字数量以50 为步长，从50 依次递增到500，对每一个关键字数量进行50 次反复实验，求出时间开销的平均值，保证实验结果的有效性。同时进行字符串字符数量与时间开销关系的实验，得到字符串的数据复杂度与时间开销无关的结论，本文实验选取8 个字母的单词作为关键字。

本文使用的数据集由复旦大学国际数据库中心自然语言处理小组提供，其中测试语料共有9 833篇文档，训练语料共有9 804 篇文档。

本节还将本文方案在区块链引入之前和引入之后进行对比实验。利用testrpc 软件进行本地以太坊网络环境的搭建，然后将本文方案编写为智能合约，并设置挖矿时间为0，以排除其他时间对结果的影响。

7.1 陷门生成时间

将本文方案与 DS-PEKS[12]、PAEKS[13]和SPE-PP[15]这3 种方案进行对比，由图2 可知，在陷门计算过程中，随着关键字数量的增加，陷门的生成时间也随之增加。对比后发现，本文方案在陷门生成时间上比其他3 个方案都有一定的优势，并且随着关键字数量的增加，优势越来越大。本文方案中的陷门生成时间不会随着关键字包含的字母数量的增多而增多，这对于查询复杂的字符串有一定的优势。同时在第6 节已经得到验证，本文方案构造的陷门满足IND-KGA 安全，关键字的安全性能够得到保障。

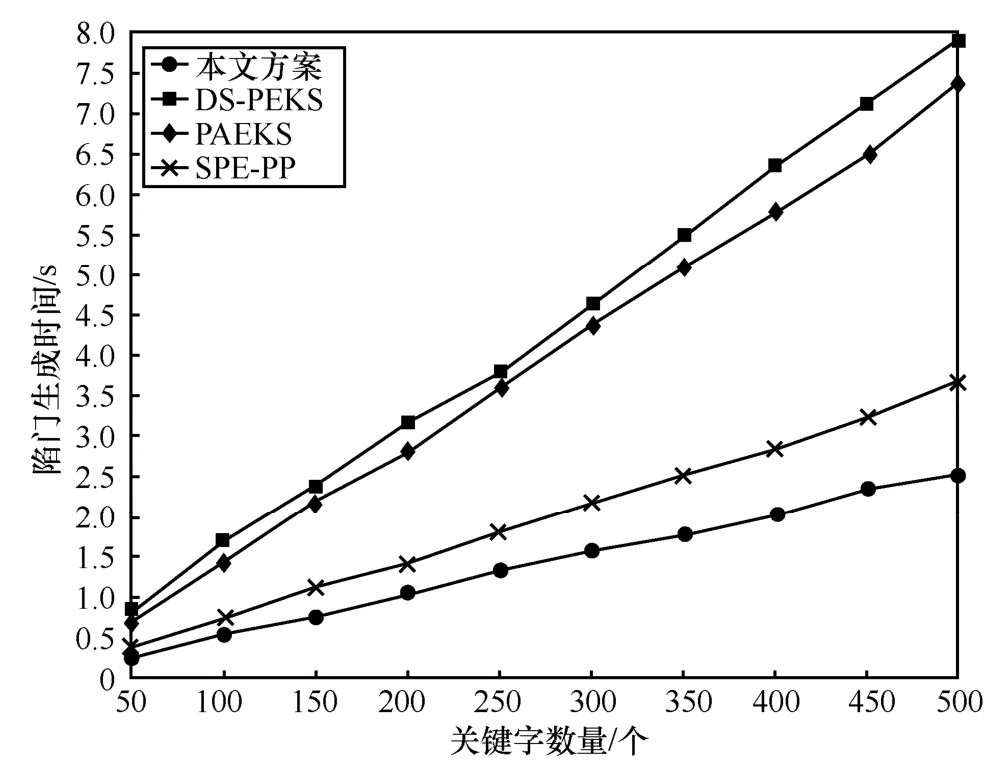
图2 陷门生成时间

7.2 索引生成时间

由图3 可知，本文方案与DS-PEKS 和PAEKS方案相比有很大优势，与SPE-PP 方案相比略有优势。造成这个结果的主要原因是本文方案中索引的计算只需要进行一次双线性计算和一次哈希计算，相比其他3 种方案，本文方案是具有更简单的构造方案。与DS-PEKS 和PAEKS 方案相比，随着关键字的增多，本文方案的优势会越来越大。

7.3 关键字检索时间

本文方案在进行关键字检索时一共进行了3次双线性对计算，相比于其他3 种方案，计算开销较小。由图4 可知，在关键字数量为500 个时，本文方案比PAEKS 和SPE-PP 方案的效率大约高25%。

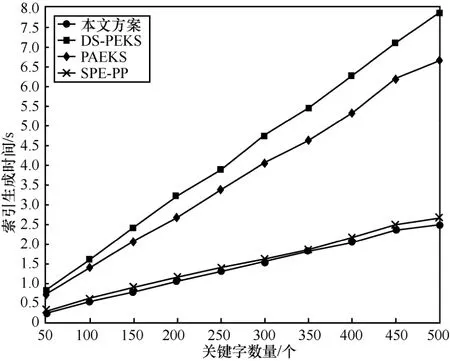
图3 索引生成时间

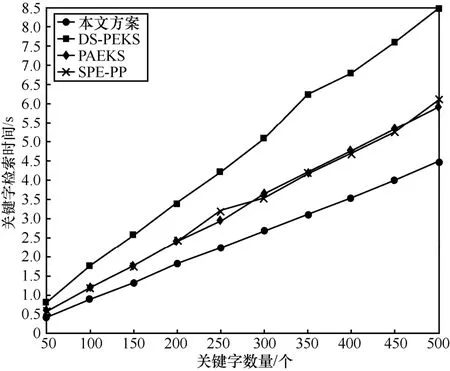
图4 关键字检索时间

7.4 区块链引入前后对比实验

区块链引入之后会导致检索时间的增加，但是增强了安全性。由图5 可知，随着关键字数量的增多，引入区块链方案的检索时间增长量逐渐减少。

图5 关键字检索时间

8 结束语

本文提出一种基于区块链的公钥可搜索加密方案，这是一种一对多的可搜索加密方案，主要应用于搭载在公共平台上的私有云环境。方案主要解决2 个方面的问题：1)保证陷门的安全性，利用DBDH 困难问题构造原则使生成索引添加的随机数与生成陷门时添加的随机数不必相同，减少了用户与数据拥有者的通信资源开销，也预防了由信道安全引起的数据泄露问题；2)利用区块链技术解决了传统方案中第三方的可信问题，同时利用区块链系统的公平公正特点，限制了服务器产生的恶意行为。安全性分析和挑战者游戏证明了本文方案的安全性。针对方案中索引生成时间、陷门生成时间、关键字检索时间进行了实验，关键字数量由50增大到500，并对每个关键字数量各进行50次实验，对得到的时间开销取平均值，与文献[12-13,15]中的方案进行对比，证明了本文方案具有较高的效率。

接下来的工作将针对可搜索加密，利用区块链技术在公有环境中进行多对多模型的研究，虽然本文能够利用区块链的高可信度，扮演权威可信机构的角色，限制服务器的恶意行为，但是在安全性与效率方面还需要进行更深入的研究。