面向水声网络可靠传输的FDR 编解码算法
2020-05-11王丽娟杜秀娟李冲
王丽娟,杜秀娟,2,李冲
(1.青海师范大学计算机学院,青海 西宁 810008;2.高原科学与可持续发展研究院,青海 西宁 810008)
1 引言
随着海洋逐渐成为人们维持可持续发展的第二领域,水声通信(UAC,underwater acoustic communication)[1-5]以其水下远距离传输的独特优势和巨大的社会效益而备受关注。陆地上的互联网通信中,不仅应用种类很多,数据量还很庞大。而对于水声通信,基本的数据传输很难保障,但是人类赖以生存的环境与海洋息息相关,人类不得不了解海洋以达到科学利用海洋的目的。克服水声通信中窄带宽、长时延、高误码率、多普勒频移、噪声及时变性的困难,通过数字喷泉码提高水下数据传输的可靠性对构建高稳健性水声网络具有重要意义[6-9]。
目前,水声网络可靠传输技术分为3 类,分别是基于重传、纠错、纠错和重传的可靠传输算法。数字喷泉码属于基于纠错的可靠传输算法。较早的面向水声网络可靠传输的机制有很多,例如,Guo 等[10]将网络编码和多径路由相结合提出了网络编码机制;Liu 等[11]提出了包级的前向纠错(FEC,forward error correction),用于可靠传输;Xie 等[12]提出了一种分段数据可靠传输方案;Liu 等[13]提出了最初的自适应可靠传输协议(ARTP,adaptive reliable transport protocol),根据节点间的距离找到合适的FEC组合,实现水下数据的可靠传输;Mo 等[14]提出了一种基于编码的多跳协调可靠数据传输机制。
数字喷泉码对中间编码信息的出错并不敏感,只关注接收端最终是否能成功译码,并且即使传输过程发生个别信息丢失也不会进行频繁的数据重传[15-16]。降低编码信息与节点、信道的相关性,是数字喷泉码适用于水声网络的一大优势。递归LT(RLT,recursive LT)码[17-18]是一种基于数字喷泉码的递归LT 码,其采用递归思想改进了LT 码的编码算法。RLT 解码算法依赖度为1 的编码分组,如果度为1 的编码分组在信道传播过程中发生丢失或误码,则解码极有可能会失败。如果在解码时从编码分组之间异或的角度出发,只要生成矩阵中2 个编码分组对应的列存在“严格短环”,那么二者即可进行异或运算。
对此,本文提出一种过滤式降维(FDR,filtering dimension reduction)译码算法,对RLT 码译码算法做出改进,弥补RLT 码的译码缺陷,提高译码成功率。FDR 算法利用生成矩阵中构成严格短环的编码分组之间的异或操作,产生度为1 的编码分组或者将高度数编码分组进行“降维”处理,使其度数降低。不会像RLT 译码算法那样,FDR 译码算法不仅解除了对来自发送端编码器产生的度为1 的编码分组的依赖,还可以快速降低高度数编码分组的度数,从而进一步降低译码复杂度。此外,本文提出了一种与FDR 译码算法相结合的优化度分布函数,在保证度为1 的编码分组数量适当的前提下,增大了高度数编码分组的选取概率,从而增加了一次降维即可得到度为1 的编码分组的概率,加快了译码进度。
本文的贡献如下。
1)对RLT 码中存在的短环问题进行数学分析,在此基础上定义、分析严格短环问题,进一步对严格短环加以利用,提出FDR 算法,解决了对度为1的编码分组的依赖。
2)提出一种与FDR 算法相结合的优化度分布函数,增加了FDR 算法在进行解码时一次降维即可得到度为1 的编码分组的概率。
3)将FDR 算法和RLT 码在NS3 仿真平台上进行大量测试,经对比分析,实验结果验证了FDR算法的有效性和稳健性。
2 相关工作
涉及本文研究内容的相关算法包括RLT 编码算法和RLT 解码算法[17-18]。
2.1 RLT 编码算法
RLT编码器能够由原始输入分组产生无限多个编码分组序列。对于给定的(k,d,Ω(d)),其中k为原始分组个数,d(d∈{1,2,3,4,k})为编码分组的度值,Ω(d)为度分布,输入分组序列为{S1,S2,…,Sk},k个输入分组构成集合I,编码分组序列为{Y1,Y2,…,Yj,…,Yn}(n>k)。编码分组与原始分组对应关系如图1 所示,具体产生过程如下。

图1 编码分组与原始分组对应关系
1)RLT 编码器对集合I中的k个输入分组先后分别执行异或操作,产生一个度为k的编码分组,复制得到个度为k的编码分组,其中pp表示水下数据逐跳传输的分组错误率。
2)从集合I中随机选取个不同的分组,构成集合U1,产生个度为1 的编码分组,其中表示期望接收到的度为1 的数据分组个数。
3)令U2=I-U1,从集合U2中随机选取个输入分组,分别与从U1中随机选取的一个分组进行异或操作,从而产生个度为2 的编码分组。
4)令U3=I-U1-U2,若,则从U3中随机选取|U3|个输入分组,从集合I中随机选取个输入分组;否则从U3中随机选取个输入分组,分别与从U1、U2各自随机选取的一个分组进行异或操作,从而产生个度为3 的编码分组。
5)令U4=I-U1-U2-U3,若,则从U4中随机选取|U4|个输入分组,从集合I中随机选取个输入分组;否则从U4中随机选取个输入分组,分别与从U1、U2、U3各自随机选取的一个分组进行异或操作,从而产生个度为4 的编码分组。
2.2 RLT 解码算法
当编码分组通过删除信道传输时,要么被接收节点正确接收,要么产生分组丢失。RLT 解码器试图从接收的编码分组中恢复原始输入分组,RLT 解码过程如下。
1)首先找到仅与一个输入分组Xi相连的编码分组Yj,若找不到,终止译码。
2)令Xi=Yj。
3)在图1 中,对每一个连接到Xi的编码分组Yj进行异或操作,即Ym=Ym⊕Xi。
4)删除与Xi相连的所有边。
5)继续从1)执行,直至解码成功。
3 RLT 码存在的问题
3.1 短环问题
停止集S[19]是满足如下条件的变量节点的集合:任意与S所包含变量节点相连的校验节点都至少2 次连接到S。停止集包含的变量节点的数量称为停止集的尺度,停止集内的变量节点构成的生成矩阵中存在短环。生成矩阵Gkn是一个k×n阶的二进制矩阵,Gkn含有n个列向量,记作Gkn=[Y1,Y2,Y3,…],列向量记作Ym=[Y1m,Y2m,…,Ykm]T,m=1,2,3,…,n,其元素的取值为0 和1。Gkn的示例为

每个列向量对应一个由k个输入分组(对应矩阵中S1…Sk)中的某几个分组异或而得到的编码输出分组Ym,如果向量元素取0 表示该输入分组不参与此编码分组的生成,如果向量元素取1 表示该输入分组参与此编码分组的生成,Ym如式(1)所示。

其中,xi表示向量元素取值。下面给出短环的定义及性质。
定义1短环。在生成矩阵中,如果有这样两列,它们在相同位置上的两行(或两行以上)均为1,这些由1 构成的行形成一个闭合的环,称为短环。
如果满足短环定义的行有两行,那么这两行构成的短环为4 元环;如果满足短环定义的行有三行,那么这三行构成的短环为6 元环,以此类推,假设满足短环定义的行有k'(2≤k' <k)个,它们构成的短环为2k'元环。以图2 所示的RLT 译码过程中出现终止现象为例解释短环。
图2(a)所示原始分组和编码分组的对应关系为Y1=S2,Y2=S2⊕S3⊕S4,Y3=S1⊕S2⊕S3,Y4=S1⊕S2⊕S3⊕S4。根据RLT 码译码过程,首先找到度为1的编码分组Y1,此时可直接译出S2并将Y1和S2之间的连线去掉,如图2(b)所示;下一步,将所有与S2相连的编码分组{Y2、Y3、Y4}分别与S2进行异或运算,同时更新Y2、Y3、Y4的值为异或运算结果,并且将它们之间的连线删除,如图2(c)所示。此时,剩余的编码分组Y2、Y3、Y4的度值d分别为d(Y2)=2、d(Y3)=2、d(Y4)=3。根据LT 码译码规则,需要找出度为1 的编码分组,但是3 个编码分组的度值均大于或等于2,所以译码被迫终止。此时,Y2、Y3、Y4对应的生成矩阵如图3 所示。
图3 的生成矩阵中包含2 个环长为4 的短环:Y3,Y4对应的两列在第一行和第三行都是1,所以第一行和第三行构成4 元短环;同样地,Y2,Y4所对应的两列在第三行和第四行都是1,所以这两行也构成了4 元短环,如图3 中虚线所示。以4 元环为例,假设RLT 码参数为(n,k,Ω),其中k为原始分组个数,n为编码分组个数,在n×k阶的生成矩阵G中重量为i的列向量在全体列向量中的比例是Ωi,也就是说,度为i的输出符号(即编码分组)在全体输出符号中的比例为Ωi[19]。
那么,生成矩阵G中某个重量为i的列向量的生成概率为[19]


图2 RLT 码译码过程中出现终止现象
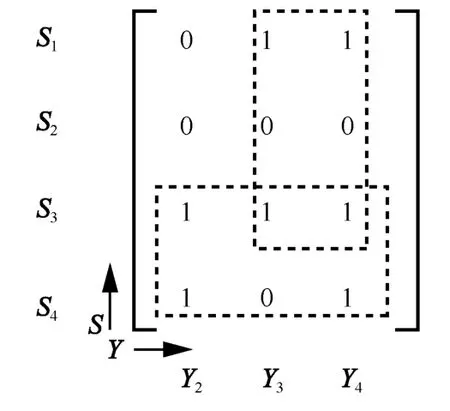
图3 Y2、Y3、Y4 对应的生成矩阵
生成矩阵G中某个重量为j(j> 1)的列向量与该重量为i(i> 1)的列向量构成4 元短环的概率为

3.2 严格短环
定义2严格短环。在生成矩阵中,如果有这样两列,它们在相同位置上的两行(或两行以上)均为1,并且其中一列除了这两行(或多行)其余位置的行上全是0,这些由1 构成的行形成一个闭合的环,称为严格短环。假设满足严格短环定义的行有k'(2≤k' <k)个,则它们构成的短环为严格(2k')元环。
生成矩阵G中重量为j(j> 2)的列和某一重量为2 的列构成严格4 元短环的概率为

根据式(4)可近似地推导出重量为j的列和某一重量为m(m<j)的列构成严格2m元短环的概率为

则对于k×n阶生成矩阵G存在严格4 元短环的概率为

根据式(6)可近似地推导出生成矩阵G存在严格2m元短环的概率为

其中,m<j。
4 FDR 算法与优化度分布函数
4.1 译码思想
在第3 节短环问题的分析中,当出现图2 所示的RLT 码译码终止现象时,3 个编码分组Y2、Y3、Y4构成的生成矩阵中包含了2 个4 元严格短环。接下来,从参与编码的原始分组集合的角度进行分析。编码分组Y2对应的参与编码的原始分组的集合为{S3,S4},Y3对应的参与编码的原始分组的集合为{S1,S3},Y4对应的参与编码的原始分组的集合为{S1,S3,S4}。这3 个集合存在明显的包含关系,即。将Y2和Y4进行异或运算可得到S1=Y2⊕Y4,将Y3和Y4进行异或运算可得到S4=Y3⊕Y4,将S1和Y3进行异或运算可得到S3=S1⊕Y3。原本使用BP 译码算法只能依赖度为1 的Y1译出S2,S2的译码运算量,而S1,S3,S4根本无法解出,可以认为,获得S1,S3,S4的译码运算量接近于无穷大,即,继而得到所有原始分组的译码运算量为。但是通过编码分组之间的异或运算,即可解出3 个原始分组S1、S3、S4。S1、S2、S3、S4的译码运算量分别为,那么成功解码所有原始分组的译码运算量为。
表面上看,严格短环是一种编码时的浪费,对传统的依赖度为1 的编码分组的解码方式并无价值,但是把译码方式进行一定改变,就可以对严格短环加以利用。严格短环的贡献将不可忽视,甚至可能成为解码剩余的未成功的原始分组的关键步骤。因此,有结论1 成立。
结论1生成矩阵中构成短环的两列只要度z值不同,并且度值较小的那一列除了构成短环的行存在1,其他行不存在1 时,它们所对应的编码分组之间即可进行异或运算。二者异或产生的新编码分组(称为二次编码分组)的度值必定小于二者之一,甚至比二者度值都小。如果二者度值相差1,它们异或直接得到一个度为1 的分组;如果二者度值相差大于1,经过异或之后,度值较大的那一列的度值可降低为二者度值之差。
LT 码译码过程要在接收到一定数量编码分组后进行;RLT 码在此做出改进,数据编码结束后首先发送度为1 的编码分组,RLT 码的译码过程在接收到编码分组之时即刻启动,但这2 种译码方式终究都是依赖度为1 的编码分组启动译码。而采用FDR 算法的译码器,在收到第一个编码分组(无论度值是否为1)后可以开始译码。仍以图2 为例,如果采用FDR 译码算法的接收端收到的第一个编码分组是Y4、第二个编码分组是Y3时,接收端对比参与二者编码的原始分组集合,2 个集合存在真包含关系,接收端便可启动译码过程,对2 个编码分组进行异或运算。因此,有结论2 成立。
结论2接收端在收到第一个编码分组时就可以启动译码过程,只要其对应的参与编码的原始分组集合与后续收到的编码分组对应的参与编码的原始分组集合之间存在真包含关系,就不必等待度为1 的编码分组,这在一定程度上缩短了译码时间。
基于以上2 个结论,本节提出一种FDR 译码算法,接下来主要介绍译码器的设计和译码流程。首先给出FDR 译码算法中的几个参数。
定义3k个输入符号向量为S={S1,S2,…,Sk},对k个输入符号进行编码产生的n个编码符号向量为Y={Y1,Y2,…,Yi,…,Yn},其中,编码分组Yi的度值表示为d(Yi)。FDR 算法将编码分组分为2 种类型,除了由k个原始分组经发送端编码器产生的n个编码分组Y1,Y2,…,Yn之外,还包括编码分组在接收端译码器内与其他编码分组异或产生的二次编码分组。为了区分,二次编码分组用Ysec表示,那么二次编码分组的度值表示为d(Ysec)。一个编码分组(无论Y1,Y2,…,Yn中的某一个Yi还是某一个二次编码分组Ysec)对应参与其编码原始分组的ID 集合为T。
4.2 译码器的设计
译码器根据编码分组的度值范围采用分层设计思想。在本文4.4 节提出的度分布函数中,编码分组的度值d(d∈ Z)有5种,分别为d=1、d=2、d=3、d=4、d=k。译码器随之设计为5 层,即l1、l2、l3、l4、lk,如图4 所示。译码器的每层分别存放的是相应度值的编码分组,在这里,层内的编码分组既包括来自接收端的编码分组,也包括来自发送端的编码分组进入译码器后在各层之间流动时与层内已存在的(先进入译码器的)编码分组异或产生的二次编码分组。比如,l2存放了所有度为2 的编码分组,这些编码分组当中可能有接收到来自发送端的度为2 的编码分组,还可能有一个度为3 的编码分组与一个度为1 的编码分组在l1层异或产生的度为2 的二次编码分组。这里还需说明的是,lk层存放度值范围为d∈(4,k]的编码分组,度为k的编码分组可以和任何一个编码分组进行异或,那么一个度为k(假设k> 8)的编码分组和一个度为t(t=1,2,3,4)的编码分组异或产生的二次编码分组的度值为k-t且k-t> 4,因此将度值大于4 且小于k的二次编码分组放入lk层。以度为4 的编码分组在lk层发生异或运算为例,产生的二次编码分组Ysec的度为d=k-4=6,所以将二次编码分组Ysec放在lk层。编码分组在译码器内的存在形式是一对key-value,key 表示该编码分组对应的参与构成其编码原始分组的ID 集合T,value 表示该编码分组。例如,编码分组Yi=S1⊕S2⊕S3,S1、S2、S3对应的ID 分别为0、1、2,即,那么Yi在l3层的存在形式为{0,1,2}-Yi。编码分组进入译码器后向下流动,依次经过译码器的各层,当到达某一层时,如果该编码分组的T和当前层内某个编码分组的T存在真包含关系,换句话说,度值小的编码分组里的所有原始数据分组同样参与了度值较大的编码分组的异或运算(此为异或条件),那么二者异或运算之后,度值较大的编码分组被更新为二次编码分组,其度值被降低。此过程相当于对度值大的编码分组进行过滤、降维,降低高度数编码分组的度值,在一定程度上加快了译码进度,度值较大或者度值很小的编码分组在某层与其他编码分组产生异或运算的概率更大。

图4 译码器层次设计
理论上,译码器的l2、l3、l4、lk层与它下面除l1层外所有层内的每一个key 不存在真包含关系。FDR译码器从收到第一个编码分组开始,一直处在解码状态,直至l1层包含整个向量S,视为译码成功。
4.3 FDR 译码流程
FDR 算法规定发送端将数据编码完成后,先发送d=k的编码分组Yn,再依次发送d=4、d=3、d=2、d=1的编码分组。具体流程如算法1 所示。
算法1面向水声网络可靠传输的FDR 编解码算法
输入编码分组序列Y={Yn,Yn-1,…,Y2,Y1}
输出原始分组S={Sk,Sk-1,…,S2,S1}


4.4 与FDR 相结合的优化度分布函数
对于给定的RLT 码编码参数(n,k),其中k为原始分组数量,n为对k个原始分组进行编码后得到的编码分组数量。编码分组的入度定义为参与其构成的原始分组的个数。
设每个编码分组的平均入度值为Dper,所有编码分组的总入度值为
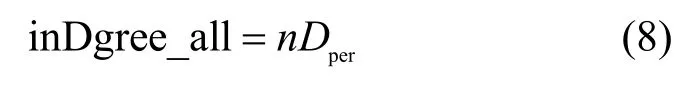
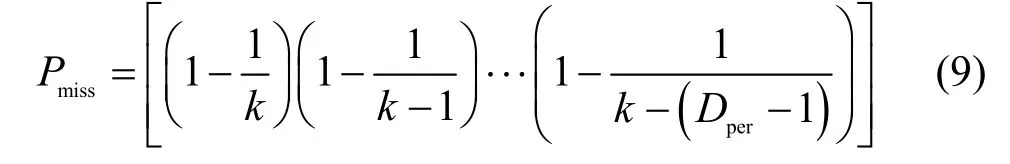
不理想覆盖问题使未被覆盖(即未参与任何编码分组的编码)的原始分组无法译出,是直接导致译码失败的主要原因之一,所以在度分布的设计中必须考虑这一点。
数字喷泉码的度分布函数影响编码复杂度,关系到编码效率。合理的度分布应该在保证度为1 的编码分组的数量适当的前提下增大度值较大的编码分组的选取概率,这样使由度分布产生的编码分组平均度值较小,同时兼顾不理想覆盖问题,保证对所有原始分组的良好覆盖。
给定k个原始数据分组,度分布设计为

其中,ρ(d)和τ(d)的计算式分别为
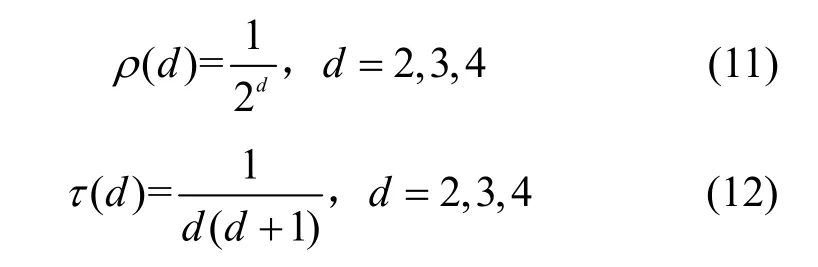
当d=1时,编码分组的数量与k相关,原始分组数量k越大,度为1 的编码分组数量越多,越有利于加快解码速度;当d=k时,编码分组数量为1,保证所有原始分组都参与到该分组的编码中,避免了不理想覆盖问题。d=2、d=3、d=4的设计从理想孤波分布出发,将度为2、度为3、度为4 的选取概率设置为小于1 的数,从而将度分布的优化转化成常数的设计问题。
由式(10)可得,度分布的期望值为
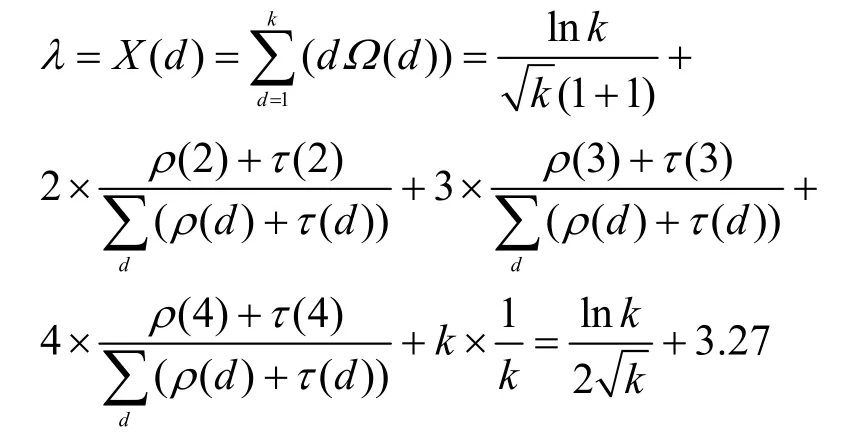
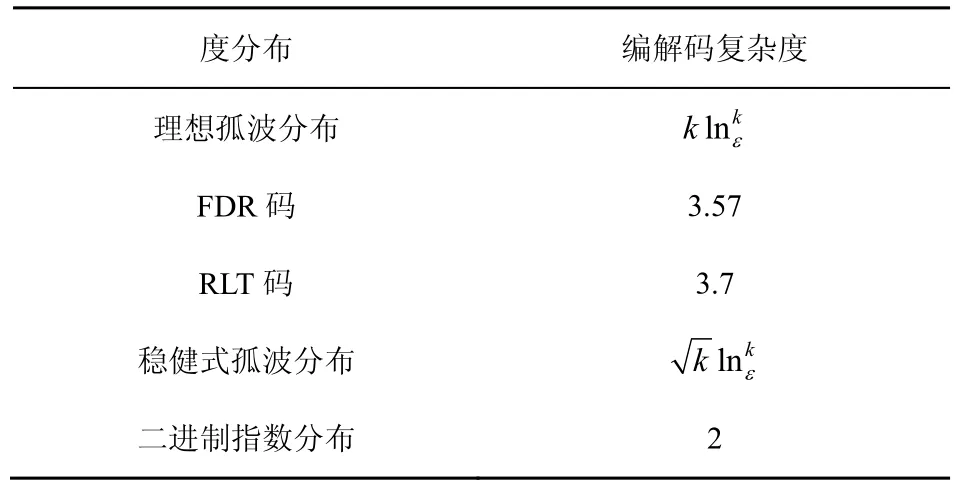
表1 几种度分布的编解码复杂度比较
4.5 编解码统计分析
将4.4 节度分布函数纳入递归编码思想中,并采用FDR 解码算法进行解码,本节从统计角度出发对解码成功概率进行如下分析。

设水声信道的纠删概率为pp,编码分组在信道上的传输符合二项分布,由概率质量函数B(N;n,pp)可知,当发送N个编码分组时,成功接收到n个编码分组的概率为

在完全随机数字喷泉码中,发送节点发送N个编码分组,接收节点成功解码的概率为
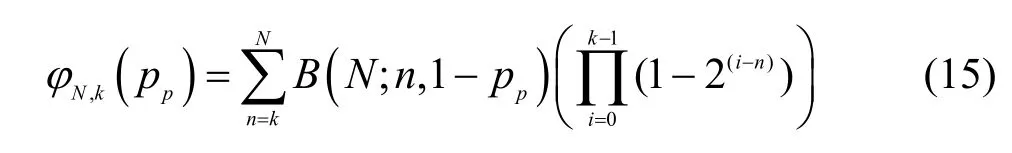
由于采用FDR 算法,k×n阶生成矩阵中满足严格短环的列向量在停止集中仍可继续被用来解码。发送同等数量的编码分组,采用FDR 算法的通信双方中的接收节点成功解码的概率要比完全随机的数字喷泉码的解码概率高。当发送节点发送N(N由式(16)给出)个编码分组时,接收节点能够恢复k个原始分组的概率由式(17)给出。
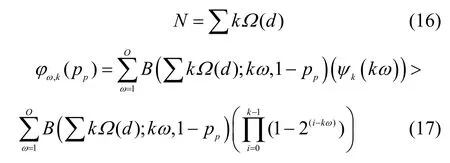
其中,O=∑Ω(d)且O> 1。
5 仿真评估
5.1 度分布仿真实验
本节采用Matlab 工具,对理想孤波分布(ISD,ideal soliton distribution)、稳健式孤波分布(RSD,robust soliton distribution)、二进制指数分布(BED,binary exponential distribution)和本文优化度分布进行仿真对比。
图5 给出当k=10 时,度值从1~10 的编码分组概率分布。图6 给出当k=20 时,度值从1~20 的编码分组概率分布。图7 给出当k=40 时,度值从1~40的编码分组概率分布。
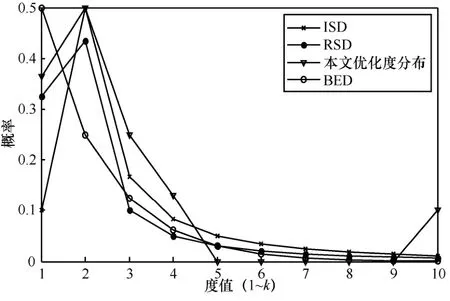
图5 k=10 时的编码分组概率分布

图6 k=20 时的编码分组概率分布

图7 k=40 时的编码分组概率分布
从图5~图7 中可以看出,采用本文优化度分布的编码分组的平均度值较低,编码分组的数量与k相关,原始分组数量k越大,度为1 的编码分组数量越多。度为1、2、3、4 的编码分组的概率较其他度分布稍大;度大于4 且小于k的编码分组数量为0。在原始分组数量较多的情况下,这样的度分布既可以控制解码不至于太复杂,又可以保证较高的解码成功概率,且无论k值如何,d=k的编码分组一直存在,这保证了所有原始分组都参与编码。
5.2 FDR 算法仿真实验
1)仿真场景
仿真实验中布置了7 个水下节点,其拓扑结构如图8 所示。其中6 个节点构成一个二维的正六边形且分别位于6 个顶点,是数据源节点;剩余一个节点是网络中的sink 节点,位于正六边形的中心。数据的流动方向是源节点到sink 节点,且它们都是单跳通信,源/目的节点间距和传输半径均为r=1 500 m。为了排除数据分组碰撞给数据恢复带来的影响,实验中设置这6 个源节点不能同时向sink 节点发送数据,这可通过控制各源节点发送分组的时间来实现。

图8 正六边形网络拓扑
2)仿真参数
实验中采用的协议架构为micro-ANP 模型,节点在应用层产生的源数据被分为多个大小为60 个数据分组的数据块,每个数据分组分为帧头、负载和帧尾3 个部分。数据分组格式如表2 所示。其中负载部分大小为200 B,尾部为FCS 校验位。

表2 数据分组格式
仿真实验的参数设置对实验结果影响较大,调整系统参数以较准确地模拟水下通信环境,如节点的发送增益。实验中,通过改变2 个节点间的距离和发送增益,测得对应距离下的发送增益值,如表3 所示。拓扑中节点间距为1 500 m,发送增益为-37 dB,节点的接收功率和休眠状态下的功率分别是0.75 W和10 mW,声波可用的频带宽度是10 kHz。

表3 传输范围与发送增益
此外,依据水下声信号衰减模型,仿真实验模拟了信号在水声信道传输时的损耗。实验采用Micro-ANP 通信架构,信号到达接收节点的物理层,接收节点计算发送增益与路径损耗的差值得出接收增益,通过判断接收增益的阈值,物理层决定这个分组是否继续向上层递交。衰减模型具体计算式为

其中,x表示收发节点间距离,a的计算式为
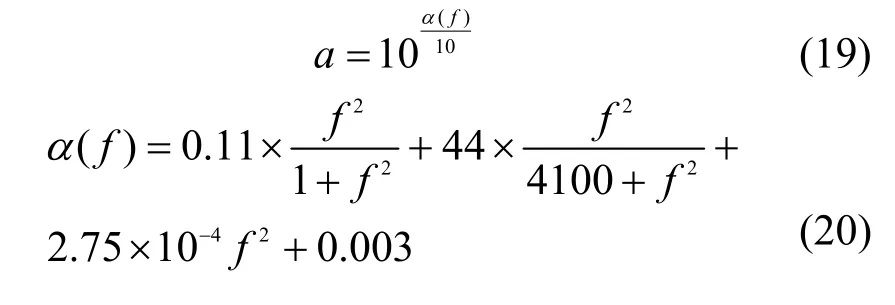
通常,能量扩散因子采用柱体扩散因子k=1.5,中心频率f=22 kHz。节点初始能量、数据块大小、仿真时间等实验参数设置如表4 所示。

表4 实验参数设置
3)仿真结果
此处定义单跳的成功解码概率,实验中可测得的数据是源节点向sink 节点发送数据的总次数NTotal-trans及经历二次编码后成功的次数Nretrans,二者之差即为单次成功传输的次数None-time-succ,None-time-succ和NTotal-trans的比值即为一次发送数据中接收端成功解码的概率,如式(21)所示。
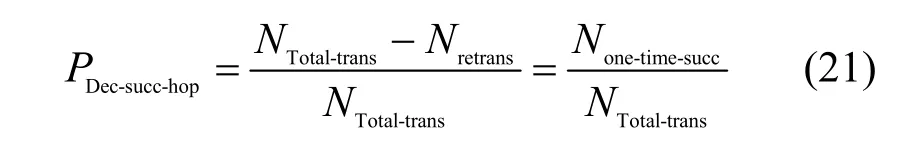
FDR 译码算法和RLT 译码算法在单次传输解码成功概率方面的仿真结果如图9 所示,其中横轴表示单次发送的编码分组数量,纵轴表示单次传输成功解码概率。从图9 可以看出,使用FDR译码算法的成功解码概率普遍高于RLT 译码算法。当编码分组数量较少时,比如n=20,2 个译码算法的解码成功概率相差无几,RLT 译码算法达到92%,FDR 译码算法可达93%。当n=25 时,FDR 译码算法出现突变情况,解码成功概率为90%,略低于RLT 译码算法的92%。当n=30 时,FDR 译码算法性能明显优于RLT 译码算法性能,二者分别为95%和89%。当n>40 时,RLT 译码算法的成功概率基本保持在86%,而FDR 译码算法的成功概率保持在89%左右。综合来看,FRD译码算法的性能较RLT 译码算法更优。

图9 RLT 译码和FDR 译码成功概率对比
实验中还统计了采用FDR 算法在不同原始分组、不同编码分组、不同发送分组频率下的4×4组NTotal-trans与Nretrans实验数据,分别如图10~图13所示。图10 显示了在0.64 packet/s 发送分组频率下,原始分组数为25、编码分组数为32 时统计的4 组实验数据。图11 显示了在0.57 packet/s 发送分组频率下,原始分组数为 30、编码分组数为38 时统计的4 组实验数据。图12 给出在0.51 packet/s 发送分组频率下,原始分组数为35、编码分组数为44 时统计的4 组实验数据。图13给出在0.70 packet/s 发送分组频率下,原始分组数为40,编码分组数为50 时统计的4 组实验数据。

图10 k=25、n=32 时的NTotal-trans 与Nretrans
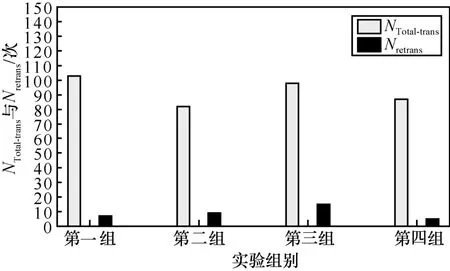
图11 k=30、n=38 时的NTotal-trans 与Nretrans
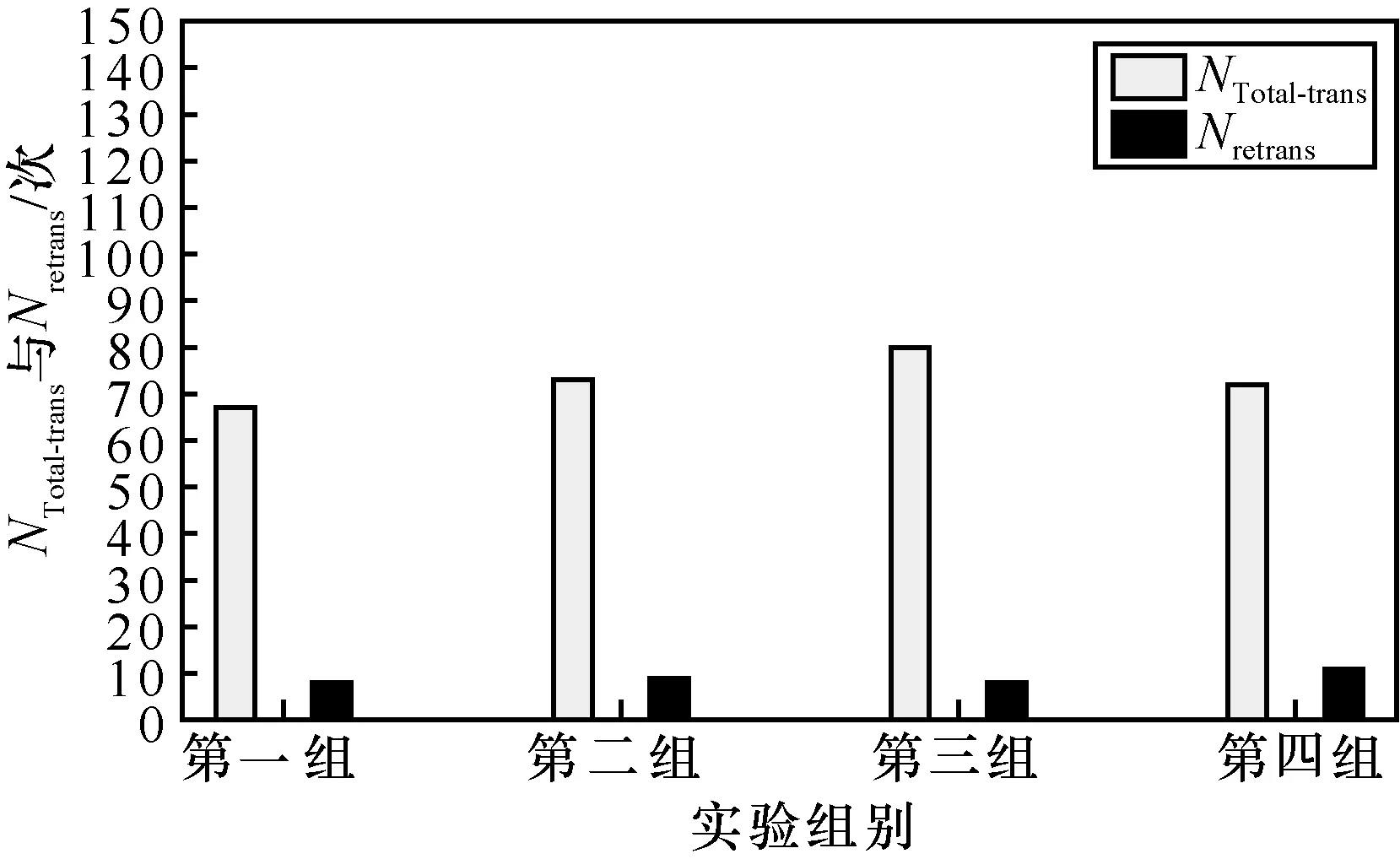
图12 k=35、n=44 时的NTotal-trans 与Nretrans
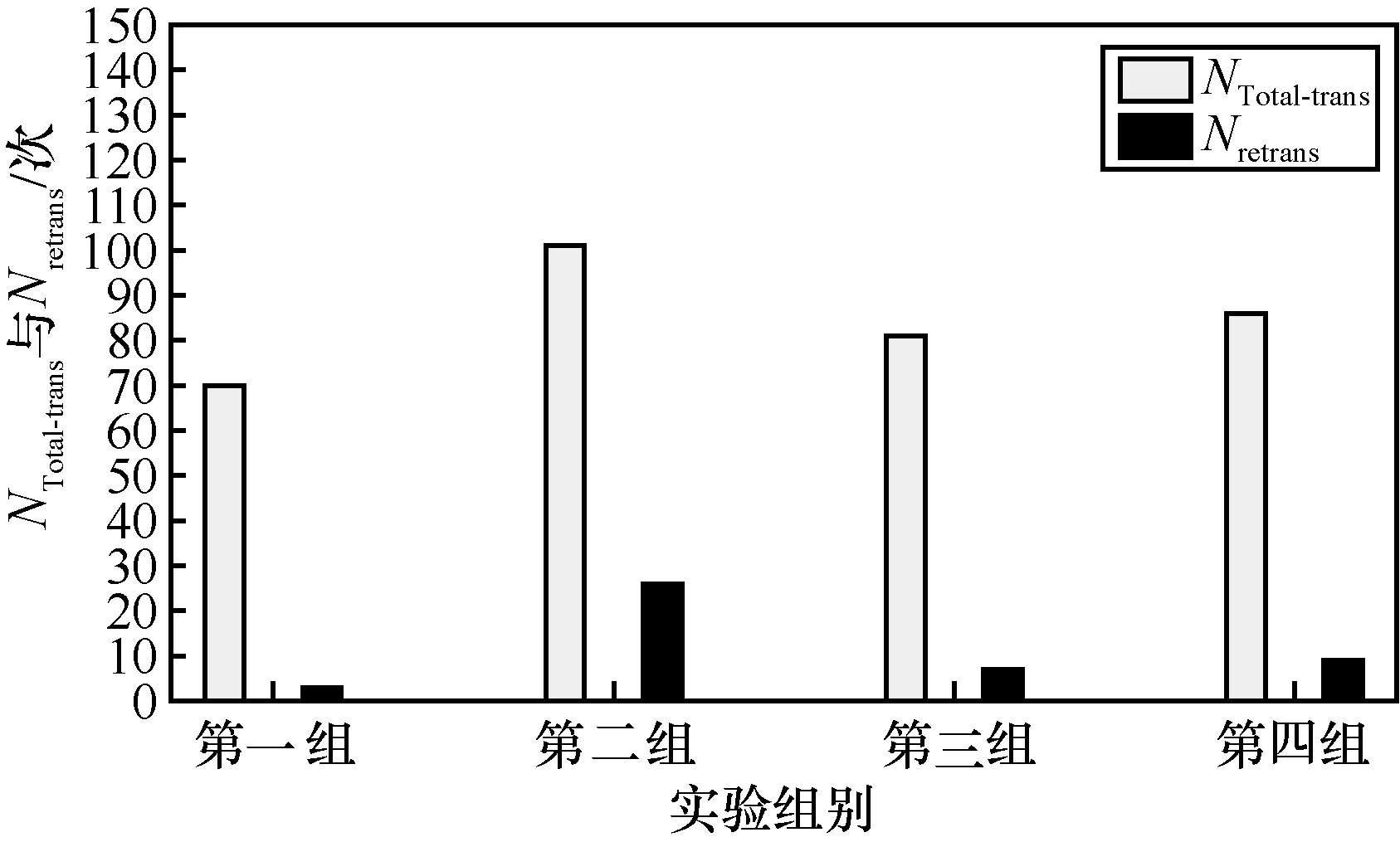
图13 k=40、n=50 时的NTotal-trans 与Nretrans
6 结束语
本文提出一种FDR 算法,消除采用传统译码方式的RLT 译码算法在收到一定数量编码分组才开始解码的等待时间,实现边接收边尝试解码的快速译码方式。此外,通过编码分组之间的异或运算,有效增加了度为1 的编码分组的产生概率,不再仅依赖于从发送端获取度为1 的编码分组,在降低传输时延的同时,通过增加度为1 的编码分组出现的概率,从而提高译码成功率。通过NS3 仿真平台在解码成功概率方面与RLT 码进行仿真对比,实验结果显示,FDR 算法的解码成功概率普遍高于RLT码,当编码分组数量为30~40 个时,FDR 算法的解码成功概率比RLT 码高5%,且FDR 算法译码成功率最高可达95%;当编码分组数量为40~60 个时,FDR 算法的解码成功概率比RLT 码高3%,且FDR算法的译码成功概率基本保持在89%~90%。实验结果验证了FDR 算法对于水声网络可靠传输的有效性和稳健性。
