斐索干涉仪中压电陶瓷的非线性校正

王 芳，卢庆杰，韩 森,2

(1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.苏州慧利仪器有限责任公司，江苏 苏州 215123)

0 引言

目前，高精密元件和高性能光学系统在科学研究和生产工程领域发挥了重要作用，而先进的检测技术和高端的检测仪器对光学元件和光学系统的制造及使用尤为重要。光学干涉测量技术是现代最精密的测试技术之一，它能快速、准确地完成对光学元件面形与系统的检测。相移干涉测量技术的基本概念是通过采集一组相移干涉图，精确地提取干涉图的相位[1-4]。压电陶瓷(PZT)致动器相移法通常被使用，即利用PZT在电压的驱动下产生位移形变的特性，使用其作为相移产生装置。但由于PZT具有严重的迟滞非线性，直接导致相邻帧干涉图之间的相移量为非线性，从而提取的相位将携带误差，影响着干涉仪的的测量结果。针对PZT的迟滞非线性问题，国内外学者已大量研究了迟滞模型(目前较成熟的模型主要有Preisach模型、Duhem模型及Maxwell模型等[5-11])及控制方法(主要有基于迟滞模型的前馈控制法、不基于迟滞模型的PID反馈控制法及前馈控制与反馈控制相结合的混合控制方法等[12-13])。

针对斐索干涉仪相移器的迟滞非线性特性，本文设计了一种基于PZT传递函数的前馈开环校正法的控制系统来校正PZT的迟滞非线性，该方法不存在反馈回路，简单有效。整个控制系统包括电压驱动系统和位移采集系统。PZT传递函数是通过PZT的输入功能函数和输出功能函数的关系来描述PZT的固有属性，然后通过结合PZT的固有属性及PZT的理想输出位移可得到PZT理想的输入电压，最终完成PZT的非线性校正。

1 系统设计

1.1 相移误差产生的相位误差

根据双光束干涉理论，干涉场中的光强分布[14]可表示为

I(x,y)=Idc(x,y)+Iac(x,y)cos[φ(x,y)+δn]

(n=-1,0,1,2,3)

(1)

式中：I(x,y)为测得的每帧干涉图像的每个像素点的光强;Idc(x,y)为光强的偏移量;Iac(x,y)为调制光强峰谷值的一半;φ(x,y)为参考波前与被测波前的相位差;δn为相移量。

测量时可得到每帧干涉图像每个像素点的光强。其中φ(x,y)，Idc(x,y),Iac(x,y)均是未知的，因此,至少需要3个干涉图才能决定在不同图像间的相位变化φ(x,y)。本文采用五步相移算法及相移量为π/2的方法来获取φ(x,y),且

(2)

式中I1～I5为每步相移后测得的光强强度。

根据δn与PZT位移量ΔL之间的关系，则式(1)可表示为

I(x,y)=Idc(x,y)+Iac(x,y)·

(3)

由式(3)可知，PZT的非线性位移将导致非等步长的相移改变量，进而产生相位误差。

相位误差σφ可表示为

(A+B+C)

(4)

式中:λ=632.8 nm为激光干涉仪的波长；ΔL1,ΔL2,ΔL3,ΔL4,ΔL5为PZT每步的位移量。

(5)

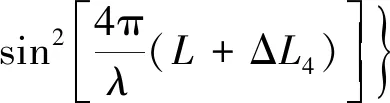
(6)

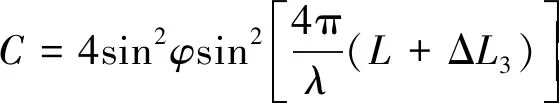
(7)

根据以上分析，相位误差可通过移相误差求得,进而可求得被测表面形貌的高度(h)误差及峰谷(PV)与起伏高度均方根误差(RMS)，分别表示为

(8)

ΔPV=Δhmax-Δhmin

(9)

(10)

1.2 实验系统

由于相位误差引起高度(h)误差，而相位误差是由PZT移相误差引起的，因此有必要提出一种控制系统和方法来校正PZT的迟滞非线性。实验研究对象PZT作为斐索(Fizeau)干涉仪相移器的关键部件，推动参考镜移动，进而产生光程差。图1为斐索(Fizeau)型干涉仪的实验平台。

图1 斐索型干涉仪实验平台

1.2.1 实验装置

图2为实验控制系统框图。实验系统采用矩形压电陶瓷叠层致动器作为驱动源。该PZT内部集成了电阻应变仪，最大输入电压150 V,行程10 μm，电阻应变仪的固有阻值为1 kΩ。数据采集设备使用NI公司数据采集卡(PCIe-6321)和连接器(SCB-68A)，主要作用是与LabVIEW系统结合产生PZT的驱动电压信号及与位移传感器、LabVIEW系统结合获取PZT的输出位移。电压放大器采用压电控制器(XE-650.OA)，放大倍率为12.5，主要作用是放大PZT的驱动电压信号。位移传感器是一个单臂惠斯通桥式电路，其中内置于PZT的电阻应变仪为其中的1个臂，其余3个臂的阻值均为1 kΩ,电阻精度均为1%。位移传感器采用5 V直流电压供电，采用MATLAB软件平台设计前馈开环校正算法程序，对采集到的位移数据进行处理，最终求出PZT理想的驱动电压值。

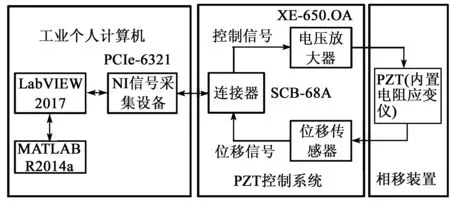
图2 PZT控制系统

1.2.2 PZT位移非线性校正控制算法

为了补偿PZT非线性特性产生的相位误差，提出了一种前馈开环控制模型校正PZT的非线性特性,开环控制思想参考文献[12],即将PZT的传递函数模型串联在PZT之前，使PZT输入与输出呈线性关系。

输入电压Vin(t)是已知的PZT驱动电压，根据干涉仪的测量要求，通过计算机、NI数据采集设备、LabVIEW系统及电压放大器产生，Vin(t)可表示为

Vin(t)=kt

(11)

式中k为常数，根据干涉仪的测量要求设置k值。

当PZT被驱动后，可得其输出位移Xout(t)，对Xout(t)信号进行多项式拟合处理，则

(12)

式中：p∈(0,P),P≥1；t∈(tm,tm+1),m=0,1,2，…；ap,P,tm，tm+1均为常数。

如果PZT的功能参数未知，则Vin(t)与Xout(t)间的关系为

Xout(t)=o(Vin(t))

(13)

式中ο为函数关系的表示符号。

同时理想的输出位移可表示为

Xideal(t)=at+b

(14)

式中a，b是常数，且a，b根据干涉仪测量要求设定其数值。

针对同一个PZT，其新的理想输入电压Videal(t)与Xideal(t)间的关系可表示为

Xideal(t)=o(Videal(t))

(15)

根据式(13)～(15)可得：

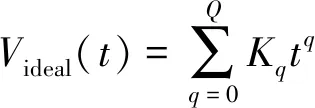
(16)

式中Kq,Q是常数，且Q>1。

1.3 实验结果

1.3.1 线性校正PZT的位移

实际中，针对干涉仪利用五步相移算法对光学样品进行表面三维形貌测量时，只使用到三角波驱动电压的正向电压驱动PZT推动参考镜产生相移，所以，此实验研究对象针对三角波驱动电压的正向电压，并对产生的位移进行线性校正。

在1.2节实验系统的基础上，系统产生幅值为100 V，频率为0.5 Hz的周期三角波信号作为PZT的驱动电压。系统的采样速率为0.5 kSPS。在系统驱动PZT时，同步采集PZT的位移数据并存储。取出PZT半个周期的位移增长数据，利用MATLAB软件平台以及1.2.2节介绍的开环控制算法，可得到PZT产生理想位移所需理想驱动电压。然后将MATLAB计算出的驱动电压值用来重新驱动PZT，系统再次采集PZT的位移数据，校正流程如图3所示。图4为PZT位移校正前、后的驱动电压值。图5为PZT校正前、后的位移值。

图3 非线性校正控制算法框图

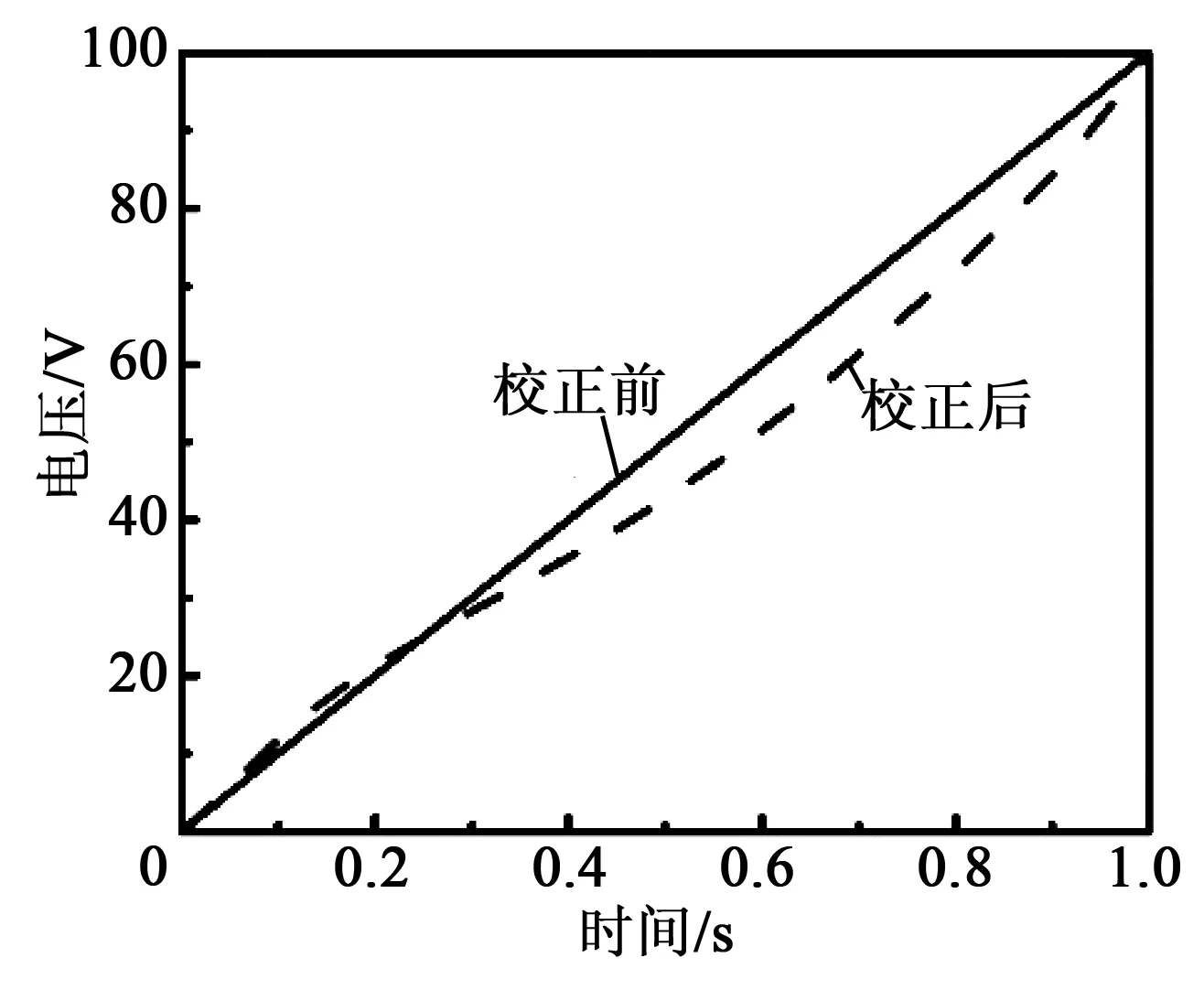
图4 PZT校正前、后的驱动电压

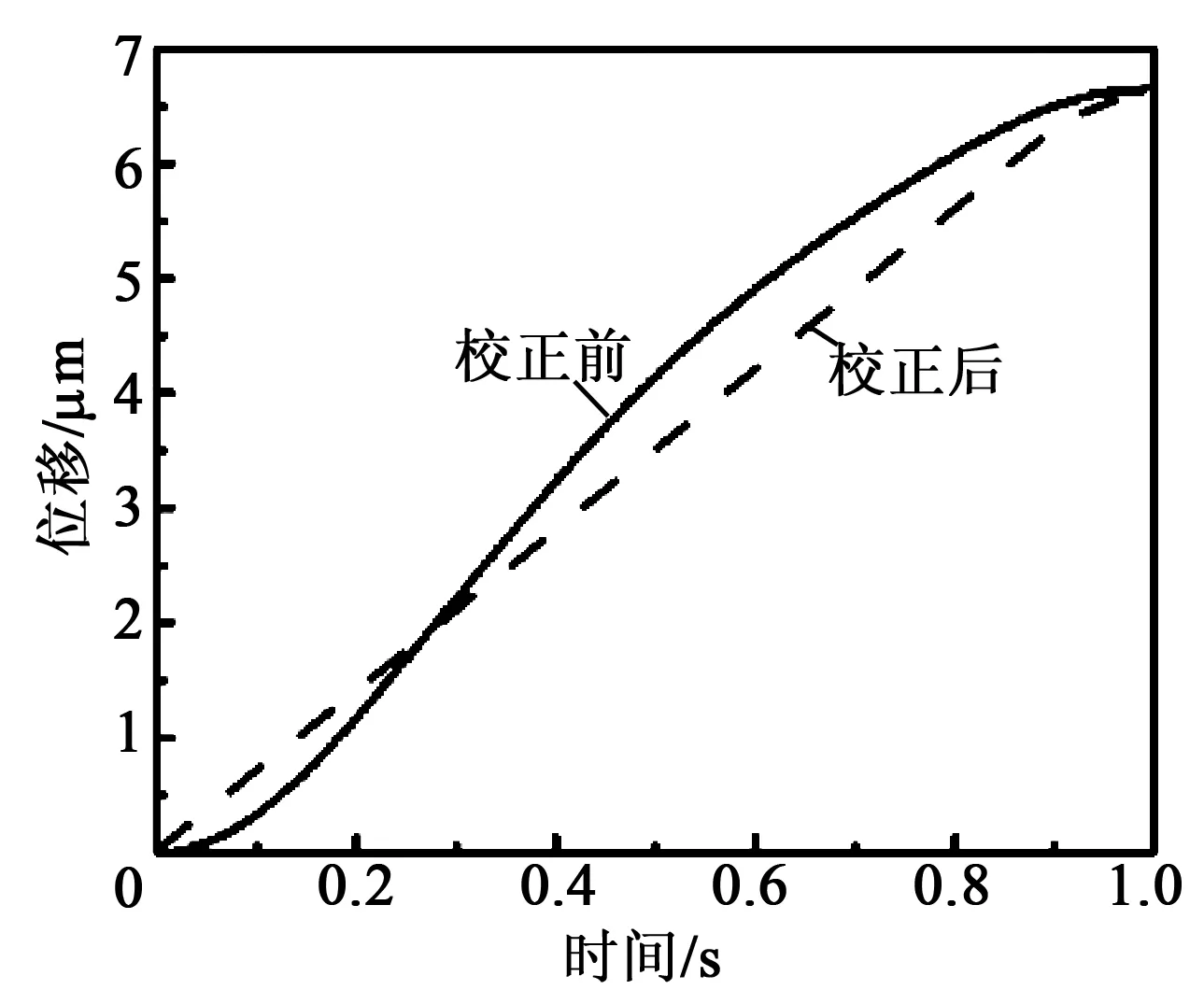
图5 PZT校正前、后的位移

图6为PZT校正前、后的驱动电压差及位移差。由图可看出，PZT校正前、后输出与输入函数呈反函数关系。

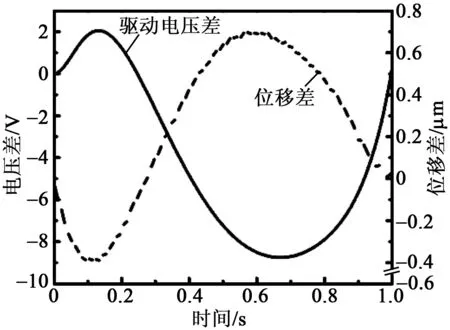
图6 PZT校正前、后的驱动电压差与位移差

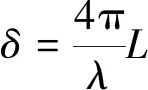
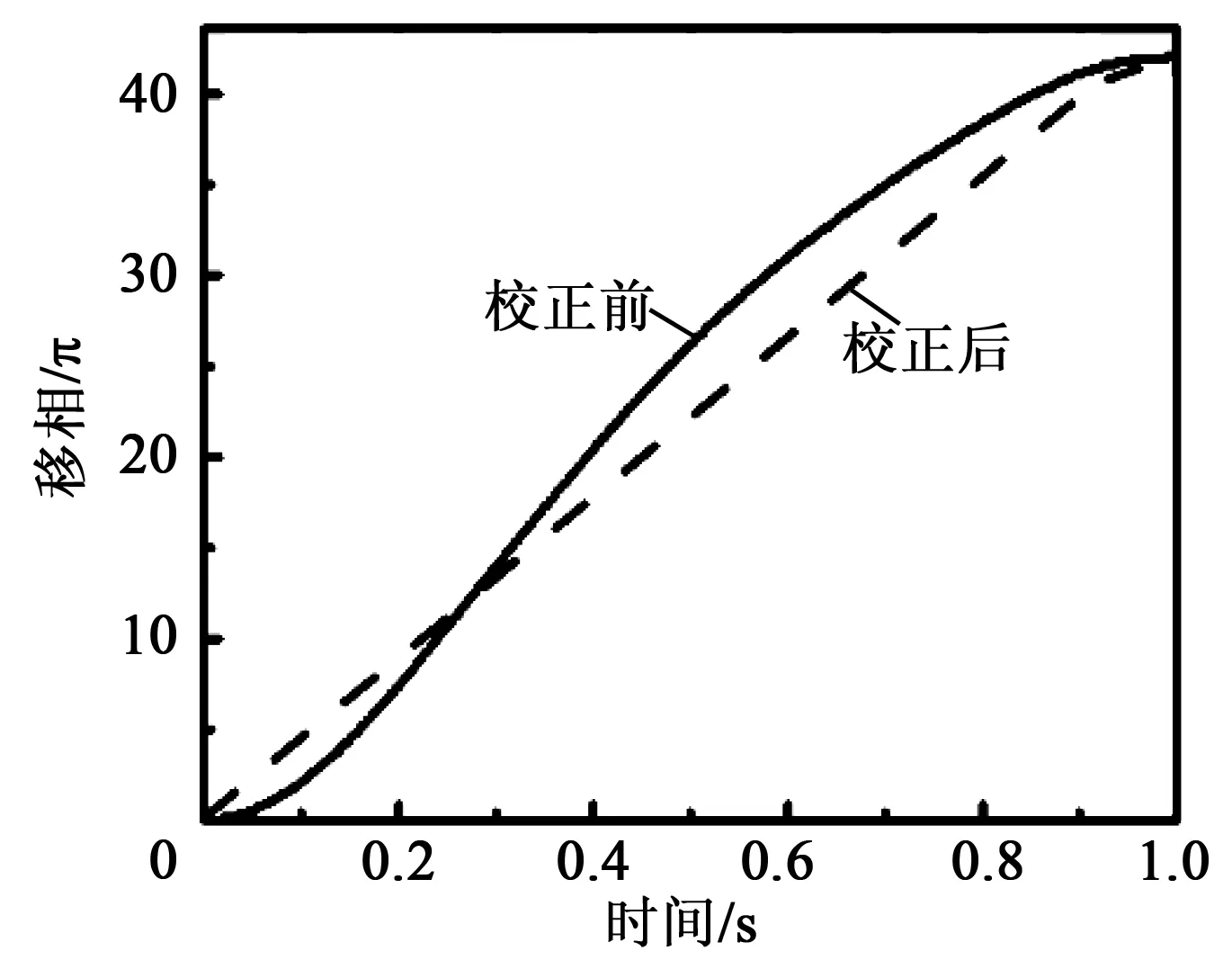
图7 PZT校正前、后相移器的移相

1.3.2 相位误差与高度误差的模拟

图8为PZT校正前、后系统的相位误差。图9为PZT校正前、后系统的高度误差。校正前，MATLAB软件编程产生32个相位值，以及5个相移误差值，系统将会产生最大相位误差为9.85×10-6rad，高度误差为4.96×10-4nm。校正后，PZT的位移轨迹为线性，在相同时间间隔内可实现每步的相移量固定为π/2，相位误差及高度误差可被改善。

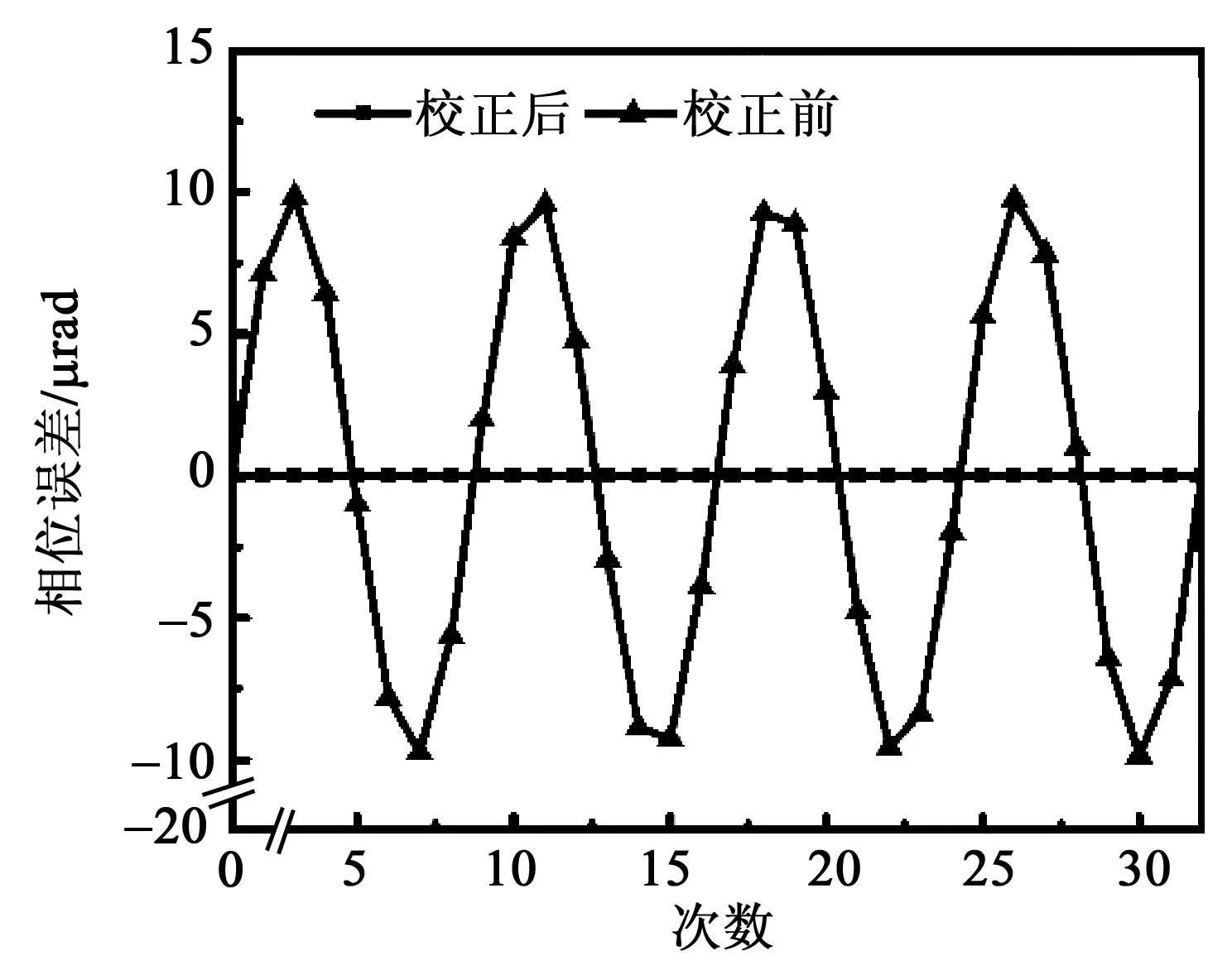
图8 PZT校正前、后系统的相位误差

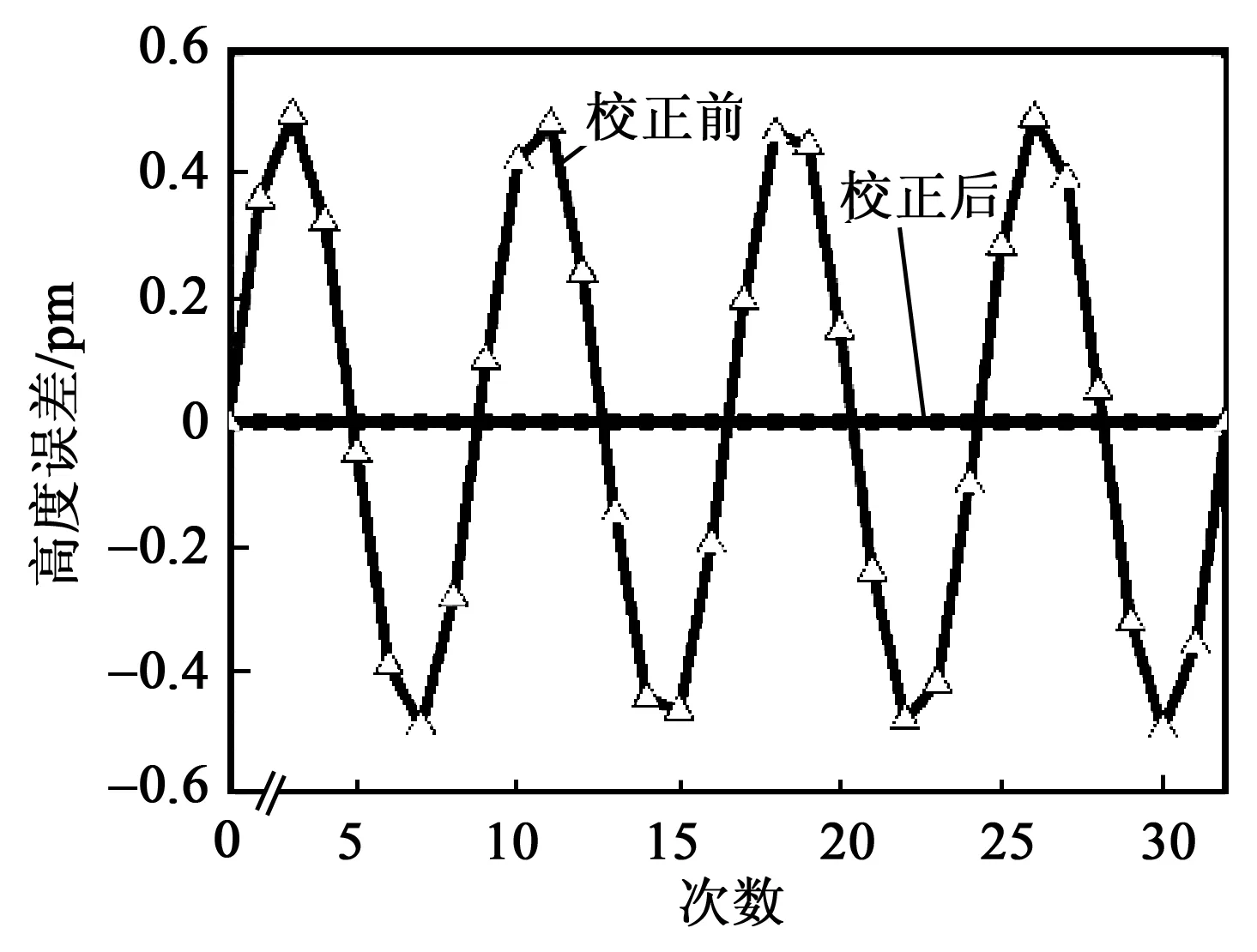
图9 PZT校正前、后系统的高度误差

2 结束语

本文结合斐索型干涉仪的实验平台，搭建了PZT相移器的控制系统，包括电压驱动系统与位移采集系统。然后结合前馈开环控制算法，可有效完成PZT的迟滞非线性校正。实验中，控制系统的采样频率为0.5 kSPS，输入电压频率为0.5 Hz。校正前、后位移差小于10%。校正后，改善了移相误差，同时改善了相位误差和高度误差，从而有效提高了干涉仪的测量精度。