BPNN辅助KF的MEMS陀螺仪数据处理方法

段志强，刘洁瑜，汪立新，李新三，沈 强

(火箭军工程大学 导航制导与仿真实验室， 陕西 西安 710025)

0 引言

微机电系统(MEMS)陀螺仪在导航、定位系统中有着重要地位，采用纯惯性导航时，由于MEMS惯性器件中存在不同类型的误差，会使导航精度随着时间的增长而不断降低[1]。提高导航精度，通常有两种办法：

1) 改善制作工艺，提高陀螺仪的精度，但此举研发周期长，成本高。

2) 通过软件补偿的办法，建立精确的误差模型，利用滤波算法提高陀螺仪精度[2]。

传统的数据处理方法有递归型数字滤波器(IIR)和非递归型数字滤波器(FIR)滤波[3]，该滤波方法需根据经验设计滤波器，且不适合噪声频谱和信号频谱混叠的情况；文献[4]利用小波去噪滤波，小波去噪中的关键问题包括阈值的确定、分解层数及小波基函数的选取，如果小波基函数的选取不合理就无法获取精确模型，将导致滤波去噪效果不理想；卡尔曼滤波因计算简单，实时性好，故在工程实践中被广泛应用，但是卡尔曼滤波在建模不精确时，易导致滤波发散，不能有效提高陀螺仪的精度。

本文针对MEMS陀螺仪误差建模不精确或难以建模的情况下，借助误差反馈(BP)神经网络辅助卡尔曼滤波[6]的思想对MEMS陀螺仪数据进行处理。将卡尔曼滤波器的新息、滤波增益、量测噪声方差矩阵引入神经网络，把系统噪声方差作为输出。通过自适应调整系统噪声方差值，得到一组较好值作为训练样本，把神经网络输出作为卡尔曼滤波的预测系统噪声方差矩阵的值，可有效提高卡尔曼滤波对外界输入的适应能力和滤波效果。

1 卡尔曼(Kalman)滤波算法分析

Kalman滤波是一套计算机实现的实时递推算法，处理随机信号有显著效果[7]。其系统的状态方程和量测方程分别为

xk=Axk-1+Buk+wk

(1)

zk=Hxk+vk

(2)

式中：xk为系统状态；zk为量测；A，B，H为已知的系统结构参数；wk为量测噪声，均值为0方差为Q；vk为系统噪声，均值为0方差为R。

卡尔曼滤波方程为

(3)

式中：Pk|k-1为一步预测均方误差矩阵；Pk为状态估计误差矩阵；Kk为系统增益矩阵。

卡尔曼滤波作为线性无偏最小方差估计滤波方法，随着时间的推移，观测数据的增多，滤波估计的精度应越来越高，均方误差阵或趋于稳定值或有界。当滤波得到的估计值可能有偏，且估计误差的方差也可能很大，超出了理想范围;其滤波误差的均值与误差趋于无穷大，导致滤波发散。

为避免滤波发散现象，本文对系统噪声方差Q进行优化处理。分析式(3)，当系统噪声太大时，Pk/k-1会越大，从而导致滤波增益Kk减小及会减小新息对最优估计值X的贡献，最终导致均方误差P变大，使滤波发散。反之，当系统的状态转移矩阵A不准确时，可以通过调节Q来使系统达到稳定。

基于以上思想，采用BP神经网络对Q进行优化，将Q设为变量，在滤波过程中进行更新，通过大量的数据对神经网络进行训练，得到一组较好的Q。在卡尔曼滤波预测时代入训练好的Q值，输出结果为最优。

2 建模与滤波器设计

2.1 陀螺仪(AR)模型建立

本文采用AR(n)模型对MEMS陀螺仪噪声信号进行建模[8]，该模型建模容易，计算快，便于预测，易估计模型的参数。系统的状态序列{xt}为0均值的非平稳随机预测值过程，且

xt=a1xt-1+a2xt-2+…+anxt-n+∂t

(4)

(5)

AR模型阶次的确定主要有自相关和偏相关定阶法、FPE 准则、模型拟合系数(AIC)准则等方法[1]。本文采用AIC准则来对AR模型进行定阶。MEMS陀螺仪漂移模型的阶次较低，一般不会超过三阶[9]。表1为AR模型系数拟合。

表1 AR模型系数拟合

根据表1可知AR(1)值最小,所以采用一阶自回归模型为

(6)

2.2 BP神经网络辅助卡尔曼滤波器设计

BP神经网络改进卡尔曼滤波器，首先对神经网络进行训练，输入层采用卡尔曼滤波器的新息、滤波增益、量测噪声方差矩阵；隐含层采用的是5层，通过误差反馈自动调节各节点之间的参数值；输出层是系统噪声方差矩阵。把训练好的神经网络进行测试，重新采集一组MEMS陀螺仪的数据，对其进行卡尔曼滤波预处理。将预处理好的新息、滤波增益、量测噪声方差矩阵输入神经网络测试，将神经网络输出的结果返回给卡尔曼滤波器，最后改进滤波器输出的值为最优估计值。

神经网络辅助卡尔曼滤波器的优势是系统模型不确定时，通过大量数据训练后的系统噪声方差矩阵具有一定的代表性，将训练好的数值直接给卡尔曼滤波器进行滤波，减少了滤波器的计算量，实时性得到进一步提升，对于短时间的捷联系统有重要的意义。建立步骤如下：

1) 结合式(6)陀螺仪的误差建模，给出卡尔曼滤波的状态方程:

(7)

2) 将实际测量与量测预测间的残差称为第k次量测获得的新息，即:

(8)

3) 滤波增益是新息的利用权重系数，且:

(9)

4) 量测噪声方差矩阵为

Rk=Py,k/k-1-HPx,k/k-1HT

(10)

步骤2)～4)作为神经网络的输入。将系统噪声方差矩阵作为神经网络的输出,即：

Qk=θ1Qk-1+θ2(Pk/k-1-APk-1AT)

(11)

式中θ1，θ2为自适应因子。对神经网络进行多次训练，得出较好的一组Q*值作为样本。

定量。并非指每日投喂数量，而是指每日根据鱼苗摄食情况、天气情况、水质状况来确定当日饲料投喂量，以饱食投喂为主。苗种培育阶段一般按照鱼类总体重5%～8%投喂，若遇到天气闷热、阴雨可以开增氧机投喂，如果都正常，没必要停喂，停喂意味着残食，影响鱼苗的成活率。

经网络采用5层隐含层，其设计流程图如图1所示。

图1 BP-KF流程图

3 实验验证

本文从静、动态数据采集两方面对本文方法进行验证。

本实验测试的BDST-MGI760-MIMU，内置的MEMS陀螺仪器件型号GRG20，带宽80 Hz；量程300 (°)/s。采样频率为100 Hz,采样周期为10 ms。

3.1 实验1

把微型惯性测量单元(MIMU)放置在恒温(25 ℃)箱里，将恒温箱放在隔离地基，通过RS232数据线连接电脑上位机。选取MEMS陀螺仪x轴为测试对象，采集过程：开机预热20 min后，采集1.5 h。获取50万个数据，截取中间的10万个作为测试数据，采集的原始数据如图2所示，x轴的均值为-0.008 5 (°)/s，方差为0.097 7 (°)2/s。

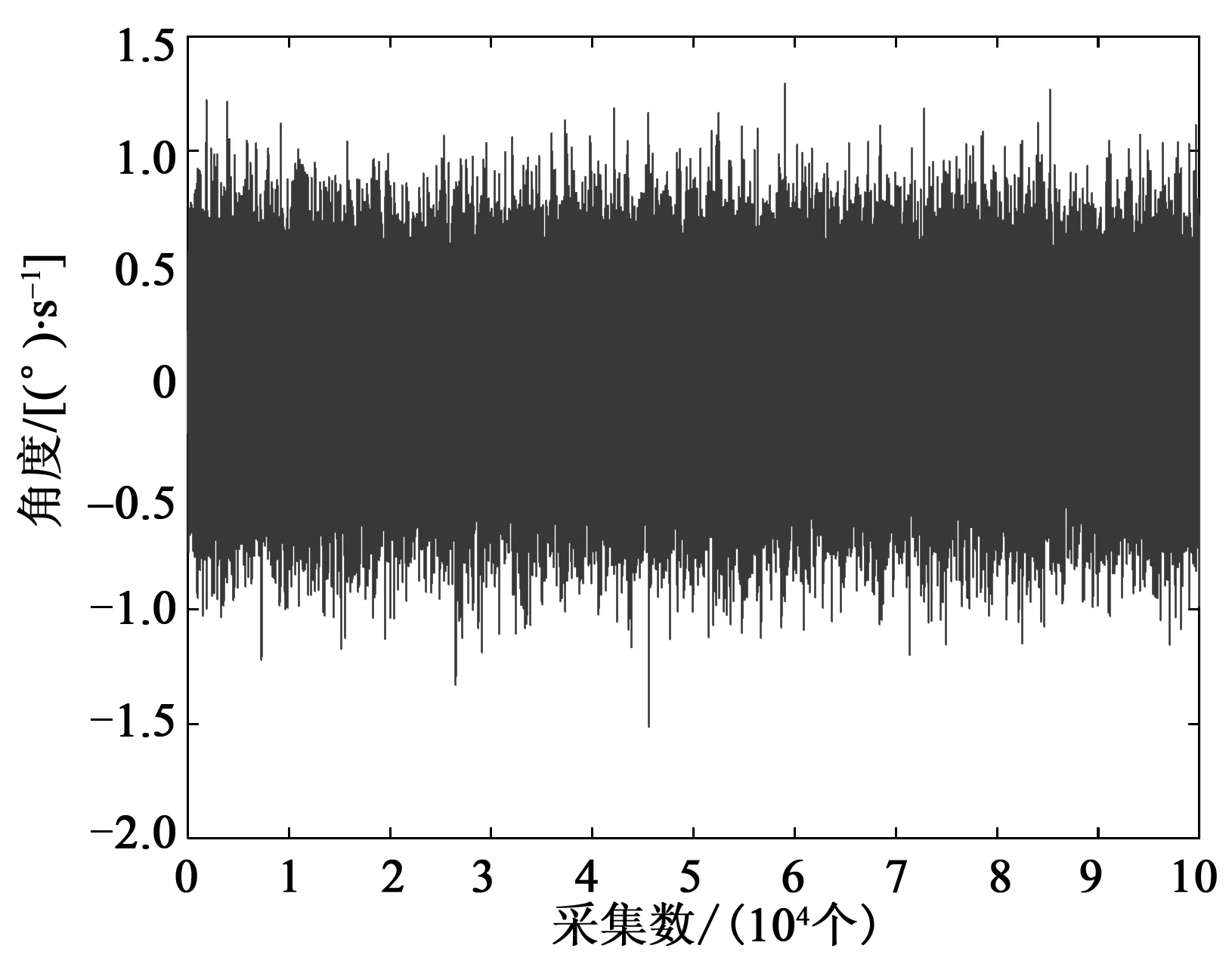
图2 原始数据

1) 预处理。将采集到的数据进行预处理，通过依达拉准则剔除粗大误差数据[10]，然后用最小二乘法提取趋势项。其均值为-0.008 2 (°)/s，方差为0.096 (°)2/s。

2) 第一次实验设计。利用第2.1节建好的数学模型设置卡尔曼滤波器，A=0.507 8，H=1，Q=0.1，R=0.01。将处理好的数据代入卡尔曼滤波器，输出结果如图3所示，其均值为-0.002 0 (°)/s，方差为0.001 1 (°)2/s。

图3 KF处理

3) 第二次实验设计。设计一组自适应卡尔曼滤波降噪实验。采用sage-husa自适应卡尔曼滤波算法，利用指数渐消记忆加权平均算法对量测噪声方差进行数值衰减。如图3所示，其均值为-0.001 3 (° )/s，方差为0.000 7 (° )2/s。

4) 第三次实验设计。采用本文第2节提出的方法，得到的结果如图3所示，其均值为0.000 46 (°)/s，方差为3.454 4×10-9(°)2/s。

采用Allan方差分析法对陀螺仪原始数据、卡尔曼滤波算法处理过的数据和BP神经网络改进卡尔曼滤波算法处理过的数据进行辨识。Allan方差(σA(τ))-对数曲线如图4所示。

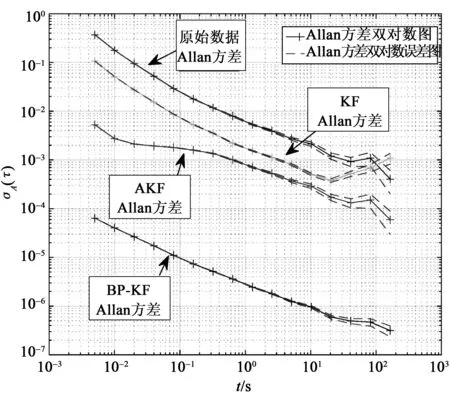
图4 Allan方差-对数曲线

设计7组不同的实验如表2所示。对MEMS陀螺仪的数据误差处理，采用Allan方差进行幅值辨识。

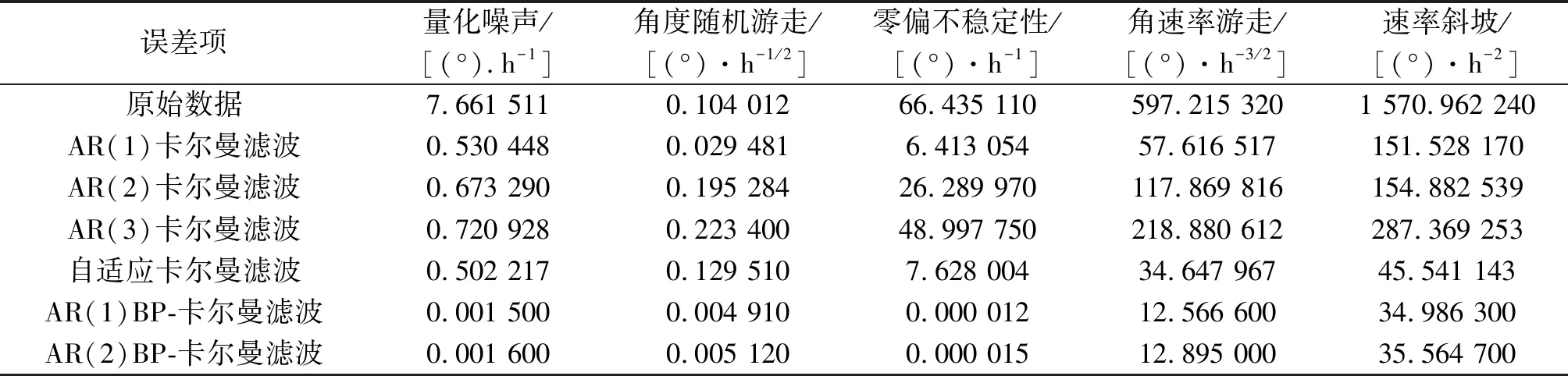
表2 Allan方差辨识结果

3.2 实验2

将微惯性测量单元(MIMU)放置在实验的双轴温控转台上，对其进行转台测试实验。截取y轴36 000个数据，将训练好的噪声协方差矩阵代入滤波方程，滤波效果如图5所示。

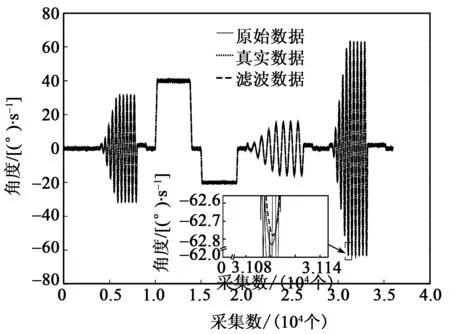
图5 转台实验数据处理

从表2可看出，使用卡尔曼滤波可使角度随机游走下降65%，零偏不稳定性下降约96%，角度随机游走，速率斜坡，量化噪声下降1个数量级。使用自适应卡尔曼滤波处理，与卡尔曼滤波相比，速率斜坡的值下降较明显，其余幅值波动不大。

在模型发生变化时可看出，模型的变化会导致卡尔曼滤波效果发生较大变动，这验证了不精确的模型会导致滤波发散情形。

BP-卡尔曼滤波算法与卡尔曼滤波算法相比，MEMS陀螺仪的量化噪声下降2个数量级，零偏不稳定性下降了6个数量级，速率斜坡下降80%，角度随机游走下降78%。且在2个不同模型的BP-卡尔曼滤波器中，得到的效果也相同(见表2)，证明了滤波器在不同模型中的适应性。

从实验2中可得出动态数据滤波后的波形较平滑，保持原始信号的基本波形。滤波前角速率误差标准差从0.496 8 ()/s下降到了0.132 6 ()/s。

4 结束语

中低精度MEMS陀螺仪随机误差较大，在使用过程中需要对其输出信息进行误差建模和降噪处理。在数据的处理过程中对陀螺仪的噪声信号建立自回归模型，采用标准卡尔曼滤波和自适应卡尔曼滤波对陀螺仪数据进行处理，与原始信号相比有显著提高，但是噪声并未完全过滤掉。为此,采用神经网络辅助卡尔曼滤波对陀螺仪数据进行了降噪处理。通过大量数据对神经网络进行训练，把卡尔曼的新息矩阵、滤波增益、量测噪声方差矩阵作为新的输入，把系统噪声方差矩阵作为输出，调节神经网络的内部参数使数据输出达到最好的效果。最后，Allan方差辨识结果表明，BP-卡尔曼滤波比卡尔曼滤波效果好，在高动态运动下也能得到较好的滤波效果。