仿生毛发气流传感器在流场中的传感特性研究

徐 强,李佳玲,孙凯旋,姜亚妮,边义祥

(扬州大学 机械工程学院，江苏 扬州 225127)

0 引言

近年来，机电传感技术获得了高速发展[1]，尤其是一些微型传感技术在医疗、家用、航空航天及人工智能等方面得到了越来越广泛的应用。随着这些传感技术的普及和应用，对传感器的使用性能和要求越来越高[2]，要求传感器可更全面与详细地对流场信号进行监测[3]，这就需要相关领域的科研人员具有更多样的思路,并提出不同的研究方法。在这种形势下，仿生学技术应运而生[4]，使得人们对于流场的分析和探究迈出了新的一步，为科研人员解决流场相关问题提供了一定的技术支持。

仿生学这一概念始于1960年[5]，经过半个世纪的发展已成为一门愈发成熟的学科[6-7]。作为一门综合性的学科，仿生学的研究方向主要是模仿自然界中生物体的生理机制，然后应用到现代科学领域中。虽然目前仿生学已获得了一定进步和发展，但还远未达到生物体的生理功能[8]，最简单的生物结构都比人工机械复杂和精细[9]，因此，仿生学还有广阔的进步空间。近年来，仿生学的应用越来越广泛[10]，与其他学科的交叉部分也越来越多，许多技术的应用实现都离不开仿生学，因此，仿生学的前景十分宽广。

研究发现，昆虫毛发作为昆虫的重要感觉器官，可以帮助昆虫感知外界的信号刺激[11]，其一般为悬臂梁结构，即一端固定在基体上，一端处于可自由运动的状态[12]，当外界信号(如气流、振动、声音等)刺激这些毛发时，毛发自由端会随着刺激信号发生弯曲并产生电信号[13]，如蟋蟀尾纤上的纤毛、蚊虫的触须及鱼类的侧线系统等[14]。本文使用的表面对称电极含金属芯聚偏氟乙烯(PVDF)纤维(SMPF)是在研究大自然生物毛发感受器的基础上，基于仿生学原理设计、制备的。目前市场上的传感器主要分为传统压电陶瓷传感器及高分子压电材料传感器[15]两种。这类传感器灵敏度较高，传感性能较稳定，但尺寸较大，很难应用于微型传感器的设计和制备[13]，制造过程繁琐，只能测试很小空间中的流场，且一旦制备好尺寸不能随意改变[16]，因此其应用场合受限。本实验采用的SMPF纤维属于高分子压电材料的一种，其压电性能好，灵敏度高，使用方便[15]，使用时可根据实验需要而改变其尺寸，制造成本低，且具有直接的压电转换性能，为仿生气流传感器的发展提供了新的思路和方法[17]。

1 仿生毛发气流传感器的设计与制备

图1为本文实验所使用的SMPF纤维结构。将金属丝置于拉丝装置中，放入PVDF颗粒加热使其融化，然后进行拉制，使金属芯表面均匀包裹一层PVDF，接着涂镀对称电极，并进行极化，即可得到SMPF纤维。

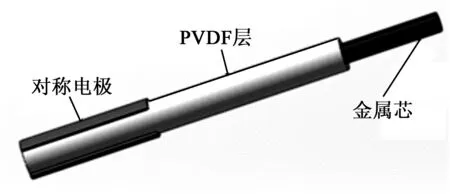
图1 SMPF纤维

2 悬臂梁结构SMPF纤维气流传感器的理论模型

SMPF纤维极化部分的压电方程[18]可表示为

S=seT+dTe

(1)

D=dT+εTe

(2)

式中:S为应变；T为应力；D为电位移；e为电场强度;s为弹性柔顺系数；d为压电常数；ε为介电常数。

实验时，SMPF纤维一端固定不动，另一端呈自由状态。当气流吹向SMPF纤维时，纤维产生弯曲(见图2)。图2中，L为纤维总长，l为纤维涂镀电极部分的长度,δ为平板不同位置流动边界层的厚度。当纤维产生弯曲时截面电极分布情况如图3所示时，两侧加粗圆弧部分为对称涂镀电极部位，气流沿着正对着电极的方向对纤维进行冲击。

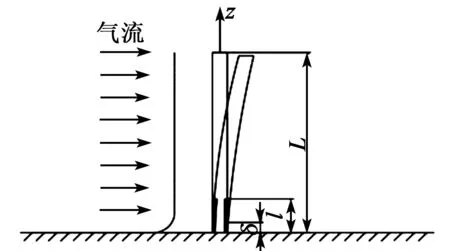
图2 SMPF纤维气流模型

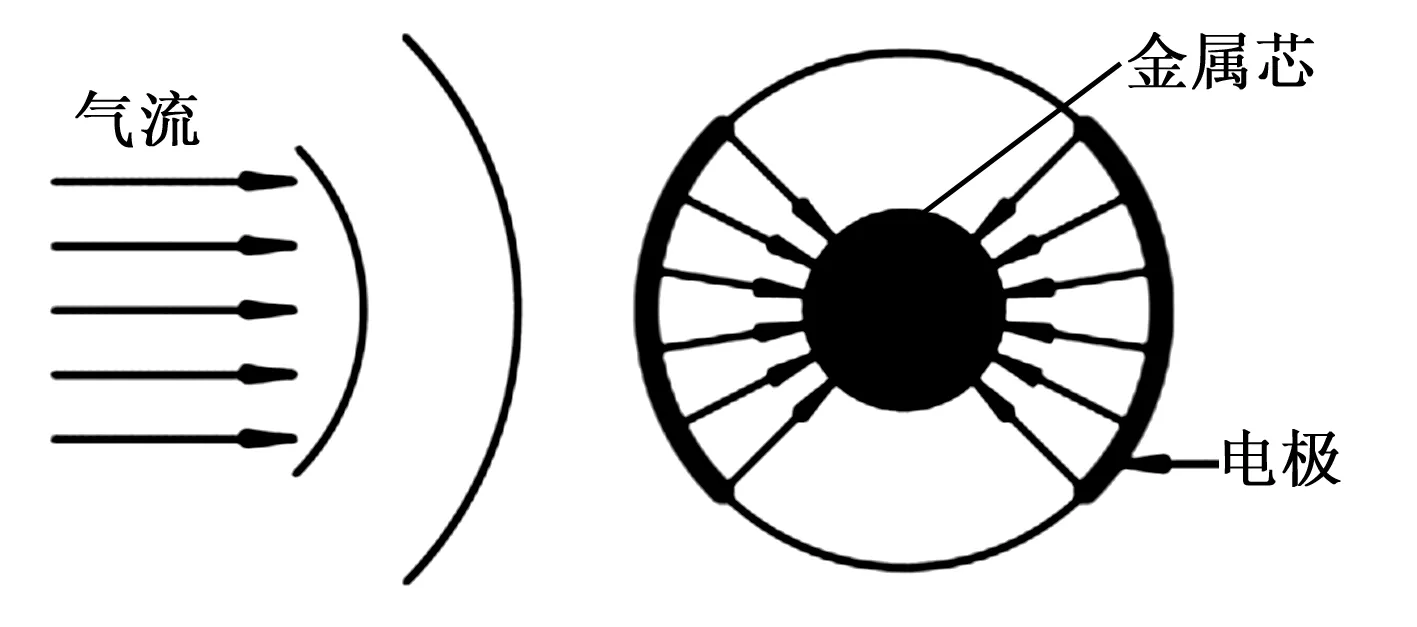
图3 SMPF纤维有电极部分截面图

当气流作用在纤维上时，纤维受到的力FD可等效为均布载荷,即

FD=CDρairv2RL

(3)

式中：FD为SMPF纤维单位长度上所受载荷[19]；v为气流速度；R为纤维截面半径；ρair为空气的质量密度；CD为阻力系数。

纤维受到的弯矩为

(4)

纤维的电位移为

(5)

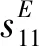
设纤维弯曲时的曲率半径为r，且只有涂镀电极的部位能产生电荷[20]，因而

1/r=M/(EI)

(6)

SMPF纤维横截面上部分电极的表面电荷为

(7)

式中：d31为压电常数；α为涂镀电极的包角。

故当给SMPF纤维一个气流冲击时，纤维会产生电荷Q，且Q与v和L呈线性增加关系。

图4为平板边界层。图中，U为沿着平板流动的气流，且初始速度为u，ux为沿着x方向的气流速度，δ1、δ2分别为平板不同位置流动边界层的厚度，τ为流体受到的切应力。当气流沿着平板方向流动时，由于流体本身具有粘性，且靠近平板处的粘性不可忽略，因此，靠近平板一侧的流速会逐渐减小，从而形成流动边界层[21]。

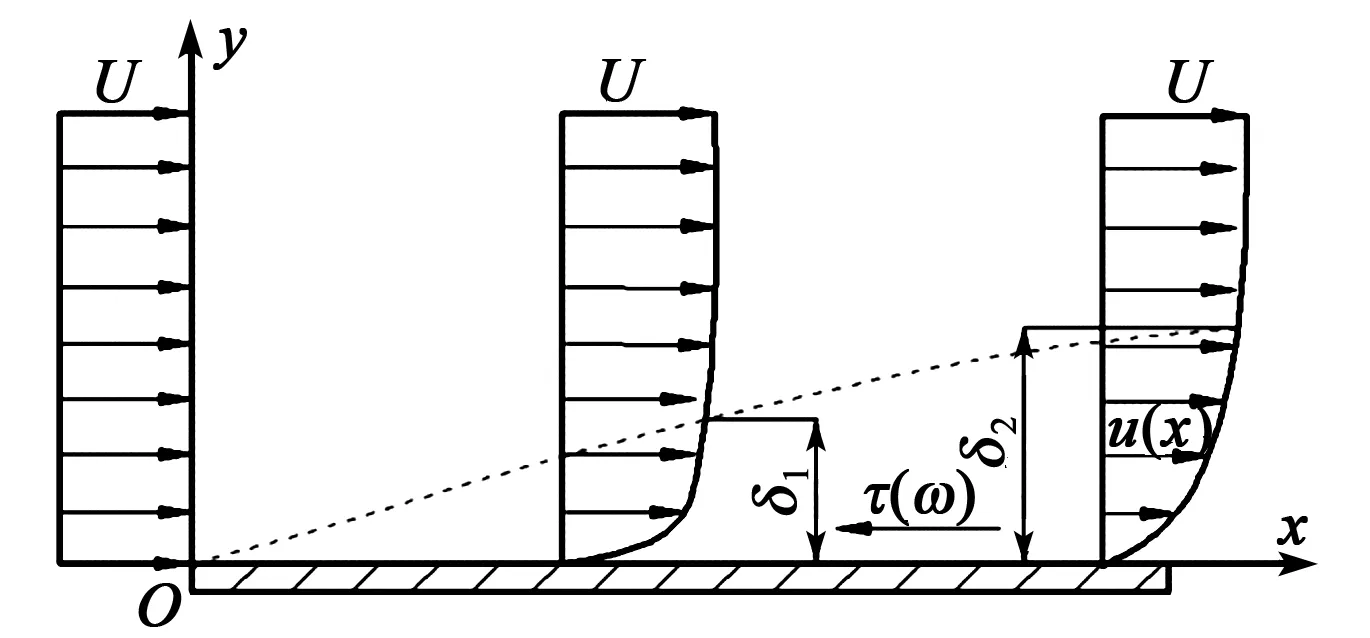
图4 平板边界层

流体在边界层处的流动满足：

(8)

(9)

则式(9)满足以下3个边界条件[18]:

1)y=0，ux=0。

2)y=δ，ux=u。

在以上3个边界条件下，速度的分布函数[15]为

(10)

边界处的切应力为

(11)

式中μ为流体内摩擦系数。将式(11)代入式(8)得：

(12)

由式(12)可看出，边界层的厚度和流体横向坐标x呈线性增加关系[14]。所以在风洞装置内沿着气流速度方向边界层厚度逐渐增加，同时边界位置的气流速度与中间位置气流速度间的差值沿着流速方向逐渐增大[21]。

3 有限元仿真分析

首先我们通过Ansys对流场进行有限元仿真分析。仿真的流体域长×宽×高为560 mm×240 mm× 90 mm，设流体的流速为5 m/s，温度为20 ℃，1个标准大气压，根据流体的流动方向设置进、出口位置，得出流体在不同位置处的气流模型得到的结果如图5～7所示。图中，突出箭头部分表示风洞流场中各截面处的速度分布，突出越明显表示所在截面两侧与中间气流速度差越大，两侧流速越小。由图可看出，在靠近第一排纤维处(见图5)位置，流场截面上各点的速度较均匀，流动边界层不明显。然后沿着流速方向，边界处的流速逐渐减小，且边界层厚度逐渐增大。说明当气流从风洞中通过时，沿着流速方向会产生流动边界层且边界层厚度逐渐增大。

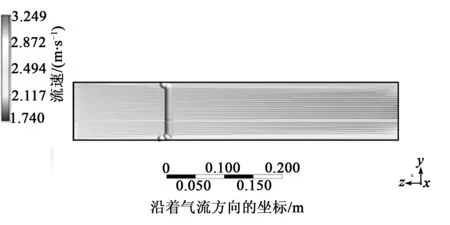
图5 第一阶段风速仿真

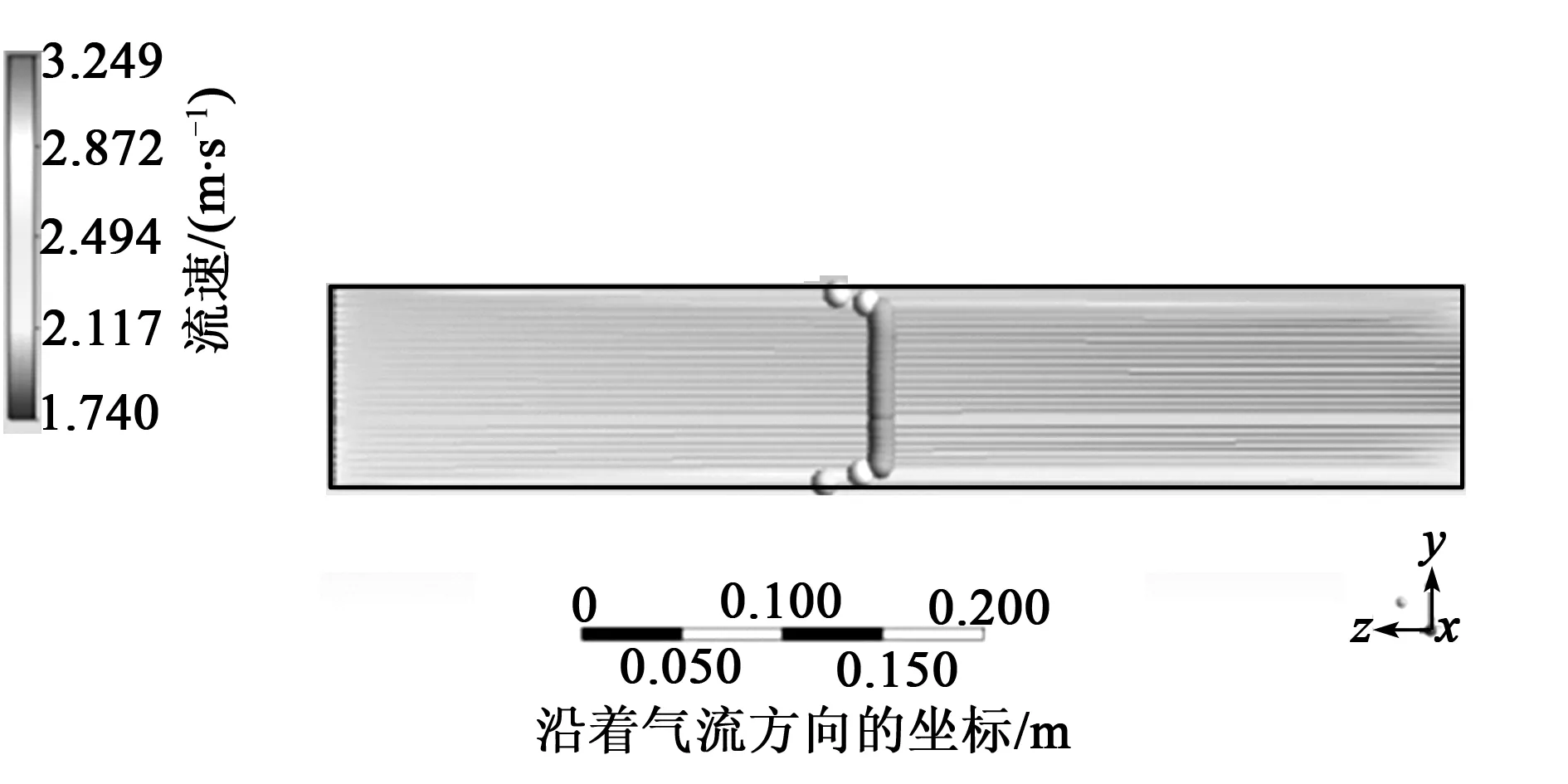
图6 第二阶段风速仿真

图7 第三阶段风速仿真

4 SMPF纤维流场传感实验

4.1 纤维对气流冲击的响应

4.1.1 单根纤维对气流冲击的响应

首先测试单根纤维能否感受流体的冲击，将纤维固定于风洞装置内，对其进行气流冲击，得出纤维输出的电信号如图8所示。由图可知，在2.652 1 s时，SMPF纤维产生电信号；在3.923 4 s时，风速传感器产生电信号；二者之间存在一个感应时间差。这是因为PVDF材料具有直接的机电转换性能。因此，SMPF纤维比风速传感器先感受到气流冲击。由图还可知，SMPF纤维产生电信号后，信号大小先增大后减小最终趋于初始状态；风速传感器产生电信号后，信号大小逐渐增大，最终达到稳定状态，说明SMPF纤维只能感受到突变的冲击信号。

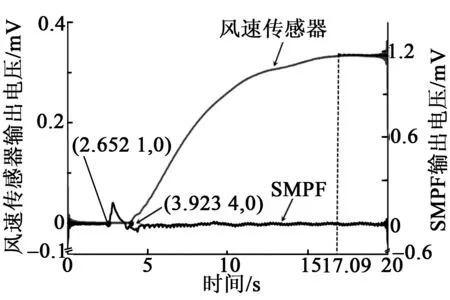
图8 SMPF纤维和管道式风速传感器实验数据对比

4.1.2 气流速度对SMPF纤维信号的影响

实验时，将纤维固定于风洞装置中，纤维长度取10 mm、20 mm、30 mm，分别用3～10 m/s的气流对纤维进行冲击。气流速度从3 m/s开始，每次增加1 m/s，对纤维产生的电信号进行采集处理，得出其随气流速度变化的关系如图9所示。

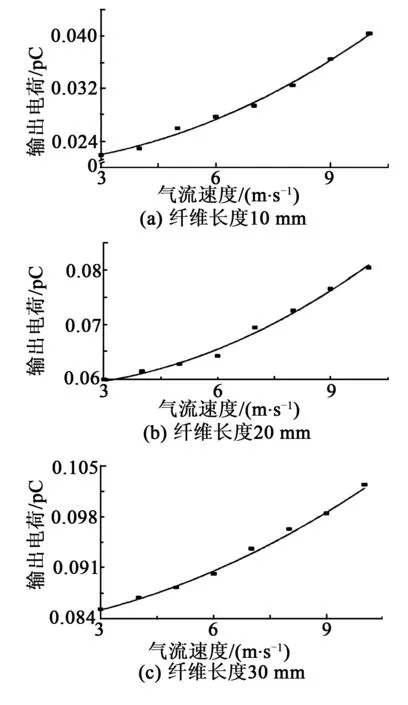
图9 不同长度时纤维信号

由图9可看出，当气流速度逐渐增大时，纤维产生的电信号逐渐增大，且二者之间呈二次曲线关系，这与式(7)的结果吻合。由图9还可看出，随着纤维长度的逐渐增加，纤维信号也逐渐增大，这与理论模型相符，即纤维产生的信号随气流速度的增大而增大，且与速度呈二次线性关系。

4.2 纤维在流场中的传感实验

4.2.1 纤维阵列在流场中的电荷变化

图10为实验装置示意图。将15根SMPF纤维呈3排5列布置于风洞实验装置中，纤维长度为30 mm，用气流进行冲击，气流速度为5 m/s。对纤维产生的电荷信号进行处理分析，分别得出每排纤维信号大小的变化规律。图11为当纤维长度和进风口处气流速度保持不变时靠近进风口处第一、二、三排纤维产生的电荷情况。

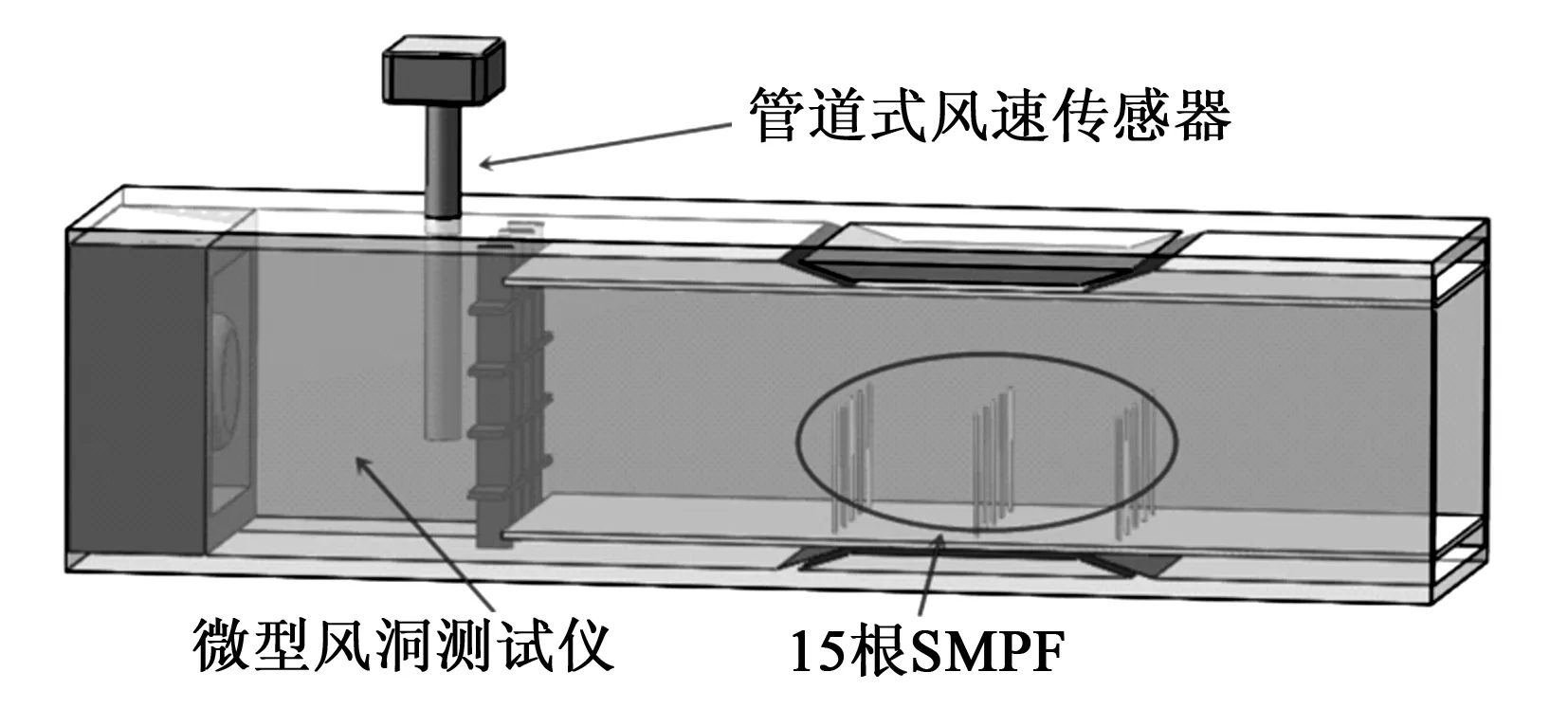
图10 实验装置图

图11 每排纤维信号大小的变化规律

图12为通过对图11进行整合分析得出的纤维阵列信号强度分布图。由图可看出，越靠近后排，两侧纤维的信号强度逐渐减小，中间纤维与两侧纤维间信号差逐渐增大。由图11可看出，对于同一排纤维，越靠近进风口处，两侧纤维与中间位置纤维间的电荷差值越小。由于纤维长度固定，由式(7)可知，影响纤维信号变化的因素为纤维所在处气流速度的大小。由此可推出，在风洞装置内，沿着气流速度方向，边界处的气流速度与中间处的气流速度之间的差值逐渐增大。由图11还可看出，对于同一列纤维，沿着气流速度方向，纤维产生的电荷信号逐渐减小，且中间一列纤维产生的电荷大小几乎不变，外侧两列纤维的电荷变化最明显。这说明在风洞装置内，沿着气流速度方向，气流速度呈逐渐减小趋势，且越靠近中间，流速减小越不明显；越靠近两侧，流速减小越明显。即沿着流速方向，气流速度整体减小，且中间处与两侧处的流速差逐渐增大。

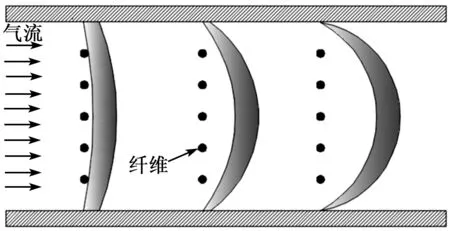
图12 纤维阵列信号大小

4.2.2 纤维阵列在流场中的响应时间差变化

由图8可看出，对同一次气流冲击，SMPF纤维和风速传感器之间存在一个响应时间差。因此，可根据响应时间差的变化来探究流场中的气流变化情况。实验装置不变，纤维仍呈三排五列布置，纤维长度为30 mm，气流速度为5 m/s，测试纤维开始响应时间与风速传感器响应时间之间的差值。对数据进行处理分析，得到二者响应时间差的变化规律如图13所示。

图13 不同排响应时间差

由图13可看出，沿着气流方向即从第一排到第三排，纤维的响应时间差曲线越来越尖锐突出。说明越靠近后排，每排居中位置纤维和风速传感器的响应时间差与同排两侧纤维和风速传感器的响应时间差之间的差值越大。由于纤维和风速传感器的位置固定不动，所以纤维和风速传感器的响应时间差是由流场内气流速度决定的，即越靠近后排的位置，流场中间处的气流速度与两侧处的气流速度的差值越大；沿着气流速度方向，流场边界处的气流速度逐渐减小，流场边界层厚度逐渐增大，图14为纤维响应时间差排布。图中每排纤维响应时间差的变化规律与图13基本一致，这也与第2节中的流场边界层理论模型相吻合。

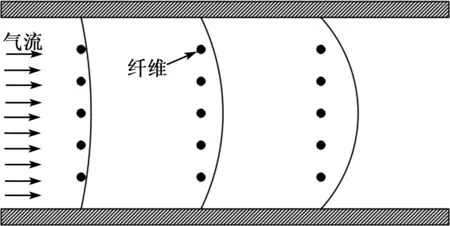
图14 纤维阵列响应时间差分布

5 结束语

本次实验先利用单根自制的仿生毛发气流传感器并将其置于风洞流场中，通过风动装置产生气流对纤维进行刺激，探究了气流速度与纤维产生电荷间的关系。然后利用多根纤维呈阵列布置于风洞装置中，在流场中对流体进行测试分析，通过纤维与气流传感器响应时间差的变化分析流场中的流体特性，得出沿着流体方向，流体边界层厚度越大，同一截面处的流体速度差也逐渐增大，并通过有限元仿真进一步验证了实验结果的正确性。为探究仿生传感器在流场中的传感特性研究提供了一定的理论基础。