力反馈模式半球谐振陀螺幅度控制方法优化

2020-05-10严隆辉蒋春桥

压电与声光 2020年2期

严隆辉，江黎，蒋春桥,杨峰，文路

(中国电子科技集团公司第二十六研究所，重庆 400060)

0 引言

半球谐振陀螺(HRG)是一种基于科里奥利效应原理的振动陀螺仪[1]。半球陀螺可工作于开环的全角模式，也可工作于闭环的力反馈模式[2]。由于力反馈模式半球陀螺寿命长，精度高及噪声低的特点，在空间领域已被大量使用[3]。

半球陀螺被激发振动后，旋转陀螺基座，受科里奥利力的作用，波腹点位置相对于基座会发生进动。半球陀螺力反馈回路通过施加力反馈控制力Cp(t)来维持波腹点在谐振子的特定位置，力反馈控制力与载体转动的角速率成正比，以此来实现载体旋转角速率的测量，其中力反馈控制力与载体转动角速率(Ω)之比称为半球陀螺的标度因数K。半球陀螺的幅度控制环路用于陀螺的振动激发和振动幅度维持，传统的幅度控制法由于外界温度变化或电子器件老化等因素的存在，使陀螺的振动幅度发生变化，从而导致K发生变化，降低半球陀螺的测量精度。本文对上述因素对半球陀螺幅度控制的影响进行了分析，并提出了幅度控制的优化方法。

1 半球陀螺力反馈模式工作原理

图1为半球陀螺等效振动模型。图中，P1为0°电极方向，P2为45°电极方向，a(t)为主振动振幅，q(t)为正交振动振幅，θ为主振动波腹与P1方向的夹角，即驻波方位角。

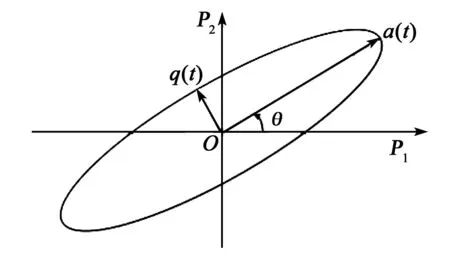
图1 半球陀螺等效振动模型

有外力作用时，半球陀螺的振动方程为

(1)

式中：P(t)为2个检测轴向的测量向量值；J为常量矩阵；f(t)为两个施力轴向的控制力向量，其由0°电极P1方向的控制力fc(t)和45°电极P2方向的控制力fs(t)两部分组成；α为半球陀螺的进动因子，其仅与谐振子球壳形状相关；ωn为谐振子的振动频率；m为谐振子等效质量。且

(2)

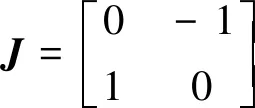
(3)

f(t)=fc(t)cos(ωnt)+fs(t)sin(ωnt)

(4)

式(1)的解可表示为

P(t)=a(t)Iν(t)cos(ωnt)+q(t)Jν(t)sin(ωnt)

(5)

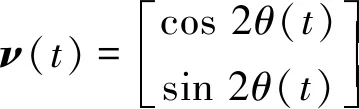
(6)

式中I为二阶单位矩阵。

将式(5)、(6)代入式(1)，忽略时间变量a(t)、q(t)、θ(t)关于时间的二阶导数可得：

(7)

Cp(t)=vTJfs(t)

(8)

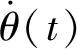
由式(7)、(8)可知，Cp(t)可改变θ，利用该特性，在半球陀螺力反馈工作模式下，可施加控制力Cp(t)使驻波方位角θ的变化率为0，即式(7)、(8)中等号左边为0，可得：

Cp(t)=-4a(t)ωnmαΩ

(9)

K=-4a(t)ωnmα

(10)

式中K为力反馈模式下陀螺的标度因数。

由式(9)、(10)可知，Cp(t)与Ω成正比，K与a(t)成正比，因此,要保持标度因数的稳定性，半球陀螺幅度控制环路需要保证a(t)的稳定。

2 半球陀螺幅度控制方式

由于各种阻尼因素的存在，需要施加幅度控制力激发陀螺振动以及维持陀螺的振动振幅，将式(5)、(6)代入式(1)可得：

(11)

Ca(t)=vTfs(t)

(12)

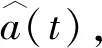
(13)

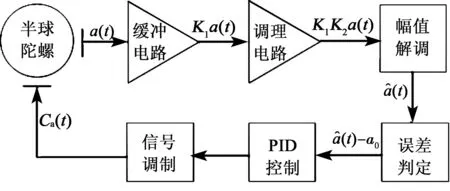
图2 传统幅度控制框图

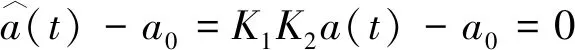
(14)

半球陀螺所处的外界温度发生改变或电子器件老化等因素,将会导致缓冲电路和调理电路的参数值(选取的电阻值、电容值等)发生改变，从而导致增益K1、K2发生改变，根据式(14)可知，这将导致主波振幅a(t)发生改变，从而导致K发生改变，使陀螺的测量精度降低。

3 半球陀螺幅度控制方式改进

针对传统半球陀螺幅度控制方式可能导致陀螺振动幅度随环境温度或电子器件老化发生变化的情况，本文对传统幅度控制进行了优化，其原理框图如图3所示。图中，Cf为积分电容。

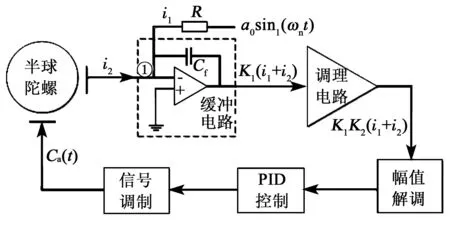
图3 幅度控制改进方式框图

对比图2、3可知，优化后的幅度控制在缓冲放大器的节点①处引入了参考电流i1，其由在精密电阻R一端施加电压信号a0sin(ωnt)来获得，即

(15)

读出电极与谐振子间的静态间隙为d0，半球陀螺工作时，由于正交振动得到有效抑制(q(t)≈0)，选取θ=0°，谐振子在波腹点的振动可表示为a(t)cos(ωnt),读出电极与谐振子间的电容C为

(16)

式中:ε为介电常数;S为读出电极的面积;U为读出电极与谐振子间的电压。读出电极的电荷Q为

(17)

由于谐振子振动产生的电流i2为

(18)

半球谐振陀螺正常工作情况下，陀螺的a(t)比d0低2个数量级[5]，式(18)可改写为

(19)

在图3中节点①处的电流为i1与i2之和，缓冲电路只是一种电流转换为电压的电路示意形式，还可选取其他形式的缓冲电路，由于在节点①已经实现了i2与i1的比较，所以图3中幅值解调的输出已是误差信号，不需要误差判定环节，幅度控制环路控制稳定后使得i1+i2=0，优化后的幅度控制方法使谐振子振动的目标值a(t)为

(20)

由式(20)可知，目标值a(t)与缓冲电路和调理电路的增益K1、K2无关，仅与产生参考电流的电阻R的阻值有关，可选取低温漂的精密电阻来保证R的稳定性。