高速磁浮列车复合材料横梁纤维褶皱问题研究

刘鹏 袁雨青 张佳卫

摘 要：高速磁浮列车横梁组成首次采用碳纤维复合材料设计，以期在降低横梁组成结构重量的同时，提高横梁组成的整体性能。主要通过复合材料曲梁强度试验对圆角纤维褶皱所造成的L形样件圆角层间强度性能下降进行对比试验验证，通过试验研究圆角分层、褶皱等缺陷对样件力学性能产生的影响，并根据层间拉伸应力理论和层间失效准则对正常状态样件的性能进行评估，通过有限元方法对正常状态样件的试验过程进行仿真模擬，从而为高速磁浮列车复合材料横梁组成工艺制造中的特定超差问题处理提供判定依据。

关键词：高速磁浮;复合材料;曲梁强度;圆角分层;纤维褶皱

中图分类号：TB     文献标识码：A      doi：10.19311/j.cnki.1672-3198.2020.09.093

0 引言

高速磁浮列车横梁组成作为磁浮车辆的主要承力构件之一，结构承载形式、载荷工况都比较复杂。目前国内外磁悬浮走行机构横梁组成全部采用铝合金材质，横梁为挤压铝型材，横梁连接件为铝合金铸件，各零件之间通过铆接工艺组装。为满足时速600km的载荷要求，有必要研制新的复合材料横梁组成。碳纤维复合材料具有比强度比模量高、可设计性强、疲劳性能好等优势，在航空航天、轨道交通领域得到广泛的应用。高速磁浮列车横梁组成首次采用碳纤维复合材料设计，结合复合材料成型工艺特点，充分发挥复合材料自身优势，以期在降低横梁组成结构重量的同时，提高横梁组成的力学性能、疲劳可靠性。

复合材料横梁外框为矩形框结构，采用阳模铺贴，阴模固化。用预浸料制作多向层压板时，通常会在圆角区域（L形件、C形件等）出现褶皱等缺陷，特别是阴模成型厚制件时这样的制造缺陷几乎不可避免。纤维分层、褶皱可能会影响最终制件的结构完整性，更严重的甚至会导致整个制件报废。

本文首先分析了圆角区域纤维褶皱的成型机理，通过曲梁强度试验验证了正常状态样件和圆角区域纤维褶皱样件的层间强度性能，确定了圆角缺陷对样件力学性能产生的影响，并根据层间拉伸应力理论计算公式、有限元仿真和层间失效准则对正常状态样件圆角位置的层间力学性能进行评估，对比了不同方法的计算精度，从而为工艺制造中的特定超差问题处理提供判定依据。

1 褶皱形成机理

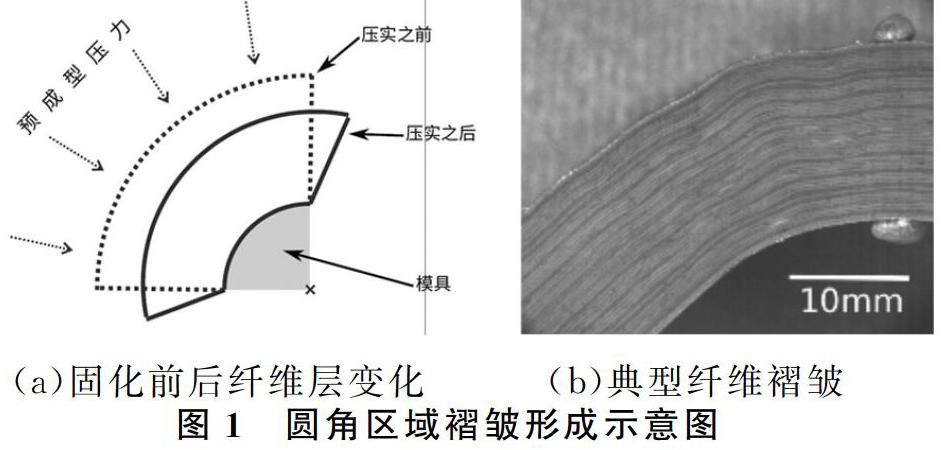
碳纤维复合材料制件是由碳纤维层预浸树脂后在模具面上逐层堆叠出来的。在这个铺放的过程中，铺层组会在适当的温度和压力下进行压实从而赶出层与层之间的空气。这个压实的过程意在保证铺层与模具面的紧密贴合同时促进层与层之间的粘接。然而，即使是在一个简单的几何面上进行压实，铺层也需要强制去适应模具面的外形。例如，考虑一个外圆角上的情况（见图1（a））。当压实的时候，相比其它层而言，最内层需要强制适应更受限的几何外形;如果铺层之间不能相对滑移，靠近模具面的这些铺层中就会形成圆周方向的压缩力，对于纤维方向和这种压缩力方向一致的铺层，它们的变形会相对较小，而其它角度铺层的变形则会相对较大（由于复合材料各向异性的特点）。如果铺层之间可以相对滑移，这种变形的不一致就会导致形成类似书本弯曲时的现象（见图1（a）），但是如果铺层之间相对滑移的阻力过大，铺层就会形成褶皱。图1（b）展示了出现在一个大尺寸构件圆角区域的轻微的纤维褶皱现象。这些褶皱不仅扰乱了纤维和树脂的均匀分布，更重要的则是会导致层间应力的增加，对制件的强度和刚度造成负面的影响，并且影响固化后制件的变形。

2 试验研究

2.1 试验件制备

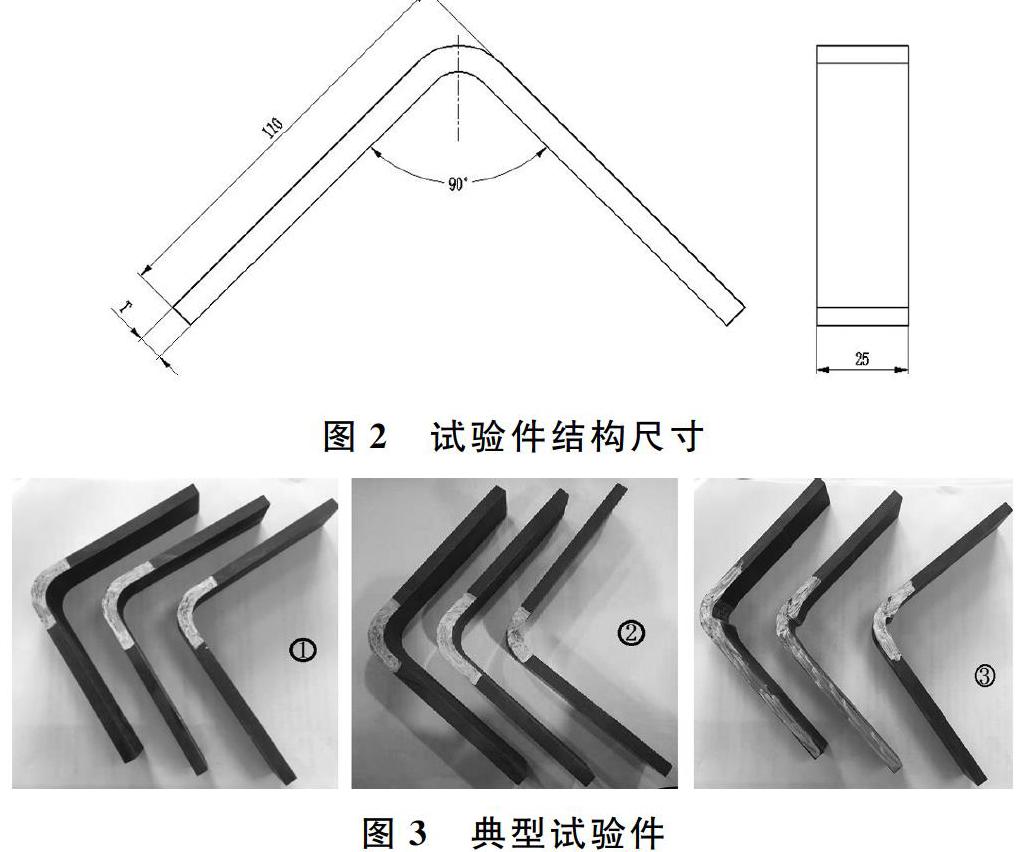
按标准ASTM D 6415-06的要求，采用与复合材料横梁相同的材料和工艺方法制备典型试验件，试验件的铺层与横梁设计铺层一致（具体铺层为[（±45）/（0/90）]8S，结构见图2。由于典型试验件弯曲部分的几何特征、表面粗糙度等对试验结果产生重要影响，按照标准的要求：试验件宽度应为（25±1）mm，受载边长度应至少为90mm并且要足够短以免触碰夹具底座，其厚度的变化不应超过名义厚度的5%，加载边的夹角应为（90±3）°。本次试验中采用的试验件受载直边理论长度为103mm（内圆角半径为9mm），理论宽度为25mm，理论厚度6.75mm，最大厚度偏差为1.05%。

曲梁强度对制件初始缺陷和空隙含量等因素极其敏感，因此本次试验中选用圆角处无缺陷、制件圆角处内部有分层、圆角处有褶皱共三种状态的试验样件，试验件如图3所示。为保证试验数据的有效性，试验件每种类型各选3件，如表1所示。

2.2 试验加载要求

（1）试验件放置在夹具之间，保证试件在加载棒之间对中。试件的侧面应垂直于加载棒，这样四个加载棒中的每一个都与试件在整个宽度范围完全接触。凭借夹具和试件的几何构型，加载后试件会在加载棒之间自动对中。然后固定在试验平台上，试验加载方式如图4所示，试验夹具各结构尺寸参考ASTM D 6415-06。

（2）加载前需要在试件侧边涂覆白色脆性涂料，以便于观察基体开裂。

（3）加载方法：连续加载，加载速度为0.5mm/min，待载荷下降到小于峰值的一半后停止试验。记录试验期间的力和位移，以便捕捉任何二次分层。

（4）试验过程中认为夹具纵向位移在5mm范围内试验件出现分层是有效的，若位移超过5mm，试验件直边的弯曲导致弯矩计算出现明显误差。

2.3 试验结果

（1）破坏模式：试验件典型破坏模式均为圆角位置的分层破坏，如图5所示。

（2）P/Δ响应：试验过程中载荷位移曲线如图6所示。

从图中可以看出，在试验夹具5mm垂向位移范围内（除编号为1-1#的一个样件略微超出外），多数试验件均出现预期的圆角位置分层破坏现象，符合标准中的规定，这表明试验数据是有效的。

综上，从表2和表3中可以看出，圆角位置有内部分层缺陷的试样的层间强度大约为圆角位置无损伤试验件的50%左右;在第3组试样中由于试件圆角位置严重的纤维褶皱问题，当所加载荷远低于正常状态样件平均失效载荷时，试验件就开始出现分层失效现象。

從表4可以看出，层间拉伸应力理论计算公式（公式（4）和公式（5））对比计算结果来看，简化近似计算公式（5）计算结果相比各向异性板理论计算公式（4）略微偏高，根据公式（4）得到的计算结果能更准确地预测试验件圆角位置的层间失效。

3 试验过程有限元仿真

3.1 材料参数

纤维层的材料是T300碳纤维织物，层压板基本力学性能中的纵向（径向）与横向（纬向）拉伸/压缩极限强度和纵横剪切强度等强度性能参数通常取B基准值，其余性能参数（模量、泊松比）均取平均值。

3.2 计算模型

采用Abaqus软件建立计算模型，试验件采用六面体单元C3D8I模拟，试验夹具为简便起见仅用刚体模拟其加载轴并划分刚体单元网格，模型中共有单元17370个，节点21108个。

3.3 边界条件和载荷

计算中对上加载轴施加强制垂向位移，固定下加载轴，试验件与加载轴之间定义接触关系（设置小的摩擦系数以限制试验件宽度方向的位移），未对试验件施加其它约束。

取铅垂向上为计算坐标系Z轴正方向，试验件宽度方向为Y轴。

3.4 计算结果

当加载不同的垂向位移时，此时试验件的变形情况如图8～图10所示（上加载轴垂向位移依次分别为-4.056mm、-4.289mm和-5.186mm）。

当加载不同的垂向位移时，此时试验件圆角部位层间拉伸应力的计算结果如图11～图13所示（上加载轴垂向位移依次分别为-4.056mm、-4.289mm和-5.186mm）。

有限元计算结果汇总后见表6。

3.5 有限元计算结果与试验对比分析

综上，从有限元仿真结果来看，所得到的试验件曲梁强度计算值基本与试验情况相符（相对试验值最大偏差为28.2%），最大层间拉伸应力计算值相比理论公式计算值偏大（相比公式（4）计算得到的最大层间拉伸应力最大偏差为38.5%，相比公式（5）计算得到的最大层间拉伸应力最大偏差为17.0%），总体而言更保守。

4 结论

本文分析了圆角区域纤维褶皱的成型机理，指出褶皱的形成不仅扰乱了纤维和树脂的均匀分布，更会导致层间应力的增加，造成分层，使制件在严重低于正常载荷的条件下出现结构失效。

通过曲梁强度试验验证了正常状态样件和圆角区域纤维褶皱样件的层间强度性能，从试验数据上来看，圆角区域较为严重的纤维褶皱可使制件层间强度性能下降超过50%。

本文同时通过层间拉伸应力理论计算公式、有限元仿真和层间失效准则对正常状态样件圆角位置的层间力学性能进行了研究，比较不同方法的计算精度，从对试验件圆角位置层间失效的预测上来看，通过理论公式（4）计算得到的最大层间拉伸应力计算结果的精度优于理论公式（5）和有限元仿真。

本文通过曲梁强度试验得到的圆角区域正常状态样件和圆角区域纤维褶皱样件的层间强度性能对比数据可为工艺制造中的特定超差问题处理提供判定依据。

参考文献

[1]Hubert P and Poursartip A.Aspects of the Compaction of Composite Angle Laminates： An Experimental Investigation[J].J Compos Mater，2001，35（01）：02-26.

[2]Lightfoot SC，Wisnom MR and Potter K.A New Mechanism for the Formation of Ply Wrinkles due to sheer between Plies[J].Composites Part A，2013，49：139-147.

[3]Potter K，Khan B，Wisnom M，Bell T and Stevens J.Variability，Fibre Waviness and Misalignment in the Determination of the Properties of Composite Materials and Structures[J].Composites Part A，2008，（39）：1343-1354.

[4]T.J.Dodwell，R.Butler，G.W.Hunt.A semi-analytical model for the wrinkling of laminates during consolidation over a corner radius[J].arXiv：Pattern Formation and Solitons，2013.

[5]Hsiao HM and Daniel IM.Effect of fibre waviness on stiffness and strength reduction of unidirectional composites under compressive loading[J].Composite Science and Technology，1996，（56）：581-593.

[6]Hsiao HM and Daniel IM.Elastic properties of composites with fibre waviness[J].Composites Part A，1996，（27）： 931-941.

[7]Garnich MR and Karami G.Finite element for stiffness and strength of wavy fibre composites[J].J Compos Mater，2004，38（4）：273-292.

[8]Karami G and Garnich MR.Effective moduli and failure consideration for composites with periodic fibre waviness[J].Composite Structures，2005，（67）：461-475.

[9]Karami G and Garnich M.Micromechanical study of thermoelastic behaviour of composites with periodic fibre waviness[J].Composites Part B，2005，（36）：241-248.

[10]ASTM D 6415-06.Standard Test Method for Measuring the Curved Beam Strebgth of a Fiber-Reinforced Polymer-Matrix Composite[S].

[11]Lekhnitskii S.G.，Anisotropic Plates[J].Gordon and Breach Publishers，New York，1968：95-101.

[12]KedwardK.T.，Wilson R.S.and McLean S.K.，The flexure of simply curved composite shapes[J].Composites，Vol 20，No.6，November 1989：527-553.

[13]R.Y.Kim and S.R.Soni.Failure of composite laminates due to combined interlaminar normal and shear stress[C].Composites86，Proceedings of Japan-U.S.CCM-III，Tokyo，Japan，1986：341-350.